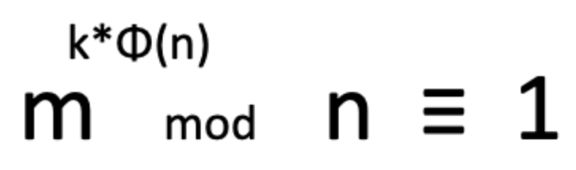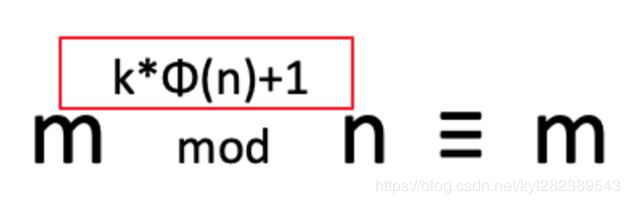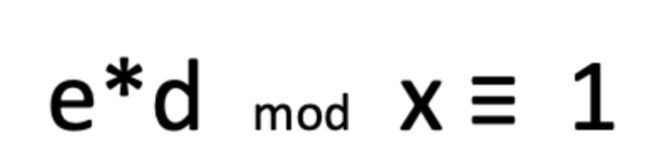IOS 逆向开发（一）密码学 RSA

@[TOC](IOS 逆向开发（一）密码学 RSA)

1. 密码学发展简介

密码学是指研究信息加密，破解密码的技术科学。密码学的起源可追溯到2000年前。而当今的密码学是以数学为基础的。

发展历史

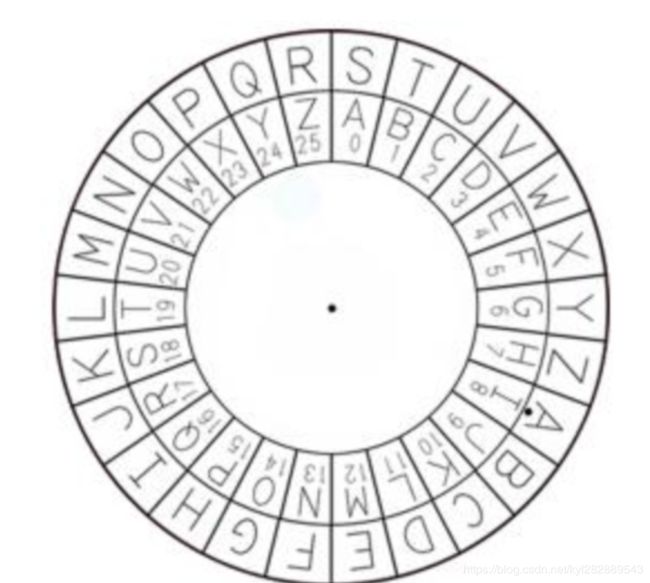
• 密码学的历史大致可以追溯到两千年前，相传古罗马名将凯撒大帝为了防止敌方截获情报，用密码传送情报。凯撒的做法很简单，就是对二十几个罗马字母建立一张对应表。这样，如果不知道密码本，即使截获一段信息也看不懂。
  

  罗马字母表
• 从凯撒大帝时代到上世纪70年代这段很长的时间里，密码学的发展非常的缓慢，因为设计者基本上靠经验。没有运用数学原理
• 在1976年以前，所有的加密方法都是同一种模式：加密、解密使用同一种算法。在交互数据的时候，彼此通信的双方就必须将规则告诉对方，否则没法解密。那么加密和解密的规则（简称密钥），它保护就显得尤其重要。传递密钥就成为了最大的隐患。这种加密方式被成为对称加密算法（symmetric encryption algorithm）
• 1976年，两位美国计算机学家 迪菲（W.Diffie）、赫尔曼（M.Hellman） 提出了一种崭新构思，可以在不直接传递密钥的情况下，完成密钥交换。这被称为“迪菲赫尔曼密钥交换”算法。开创了密码学研究的新方向
  

  密码学牛人
• 1977年三位麻省理工学院的数学家 罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起设计了一种算法，可以实现非对称加密。这个算法用他们三个人的名字命名，叫做RSA算法。

2. 非对称加密RSA产生过程

• 上世纪70年代产生的一种加密算法。其加密方式比较特殊，需要两个密钥：公开密钥简称公钥（publickey）和私有密钥简称私钥（privatekey）。公钥加密，私钥解密；私钥加密，公钥解密。这个加密算法就是伟大的RSA
• 这种算法非常可靠，密钥越长，它就越难破解。根据已经披露的文献，目前被破解的最长 RSA密钥是 768 个二进制位。也就是说，长度超过 768 位的密钥，还无法破解（至少没人公开宣布）。因此可以认为，1024 位的 RSA 密钥基本安全，2048 位的密钥极其安全。
  ( 当然 RSA 的缺陷也很容易想到 : 效率相对较低 , 字节长度限制等 . 因此实际应用中我们往往会结合对称性加密一起使用 , 关键内容使用 RSA )

3. RSA 数学原理

3.1 离散对数问题

3.1.1 原根

• 先从一个问题开始：三的多少次方模 17 等于 12?

  
  
  

  3模17

• 显然 , 对于离散对数问题 , 其正向计算得到右边 12 很简单. 但是反向运算时 , 就无从下手. 只能穷举 .

• 而且当模数使用质数 17 时 , 结果固定在 1 ~ 17 之间. 而当 17 这个模数足够大时 , 就算知道采用的是这个算法 , 也知道 17 这个质数和答案 , 想要再计算出来上图中这个问号值 , 可以想象到其难度和计算量有多大 .

• 如下图：

  
  
  

  17的原根

• 从上图我们可以看出，3的N次方取模17的结果是范围：从1到16的任意一个数字。这样3称为17的原根。

• 这样我们得出一个规律用来加密，3 的 N次方，也就是上面图的
  

  3模17
  
  

  的问号，我们可以用作N（公式中的？号）作为明文，得到密文 12 。这样即使黑客得到我们在网络中传输的密文12 ，就是他知道这个公式，他也很难反算出我们的明文 N。特别是我们把被模数17改的更大一些，如改为几百位的数字，那么黑客基本上是不可能通过这个公式反算出我们的明文的。他只能通过不断试错的暴力破解方式。

• 通过上面这个公式反算，计算出明文N的问题叫做离散对数问题

3.2 欧拉函数Φ

先了解一些概念

• 关于互质关系：如果两个正整数，除了1以外，没有其他公因数，我们就称这两个数是互质关系（coprime）。

如果一个数N是质数，那么小于N的数都会与N 这个数字互为质数。如N=5，那么1，2，3，4都与5构成互质关系，那么 Φ(5) = 4，表示有4个数与5构成互质关系。

• 任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？计算这个值的方式叫做欧拉函数，使用：Φ(n)表示
  • 如: 计算8的欧拉函数，和8互质的 1、2、3、4、5、6、7、8，Φ(8) = 4
  • 计算7的欧拉函数，和7互质的 1、2、3、4、5、6、7，Φ(7) = 6
  • 计算56的欧拉函数，Φ(56) = Φ(8) * Φ(7) = 4 * 6 = 24

通过上面的一些推理，我们不难发现欧拉函数的特点：

• 欧拉函数特点
  • 一、当n是质数的时候，Φ(n)=n-1。
  • 二、如果n可以分解成两个互质的整数之积，如n=AB则：Φ(AB)=Φ(A)*Φ(B)
  • 根据以上两点得到：如果N是两个质数P1 和 P2的乘积则： Φ(N)=Φ(P1)Φ(P2)=(P1-1)(P2-1)

例如 15 = 3 * 5 ，Φ(53)=Φ(5)Φ(3) ， 而 Φ(5) = 4，Φ(3) = 2， 则Φ(53)=Φ(5)Φ(3) = 4 * 2 = 8， 也就是15有8个数与它构成互质关系。

3.3 欧拉定理

• 欧拉定理：如果两个正整数m和n互质，那么m的Φ(n)次方减去1，可以被n整除。(m^Φ(n)-1)/n = K(整数)
  
  

  欧拉定理公式
• 费马小定理：欧拉定理的特殊情况：如果两个正整数m和n互质，而且n为质数！那么Φ(n)结果就是n-1。(m^(n-1)-1)/n = K(整数)
  

  费马小定理

3.4 公式转换

模反元素：如果两个正整数e和x互质，那么一定可以找到整数d，使得 ed-1 被x整除。那么d就是e对于x的“模反元素”

模反元素

如上图所示，转换过程5步即可：

1. 首先根据欧拉定理

   
   
   

   首先根据欧拉定理

2. 由于 1 的 k 次方恒等于 1 , 那么

   
   
   

   由于 1 的 k 次方恒等于 1

3. 由于 1*m ≡ m , 那么

   
   
   

   1*m ≡ m

4. 用模反元素转换，那么换算成公式 就是:

   
   
   

   用模反元素转换

5. 转换一下写法

   
   
   

   转换一下写法

6. 比较第五步和第三步中红框部分. 也就是说当 x 等于 Φ(n) 时 :

   
   
   

   比较第五步和第三步中红框部分

d 是 e 相对于 φ(n) 的模反元素
注意 : 公式推导第一步时 我们欧拉定理的前提是 m 和 n 互质 , 但是由于模反元素的关系 , 其实只要满足 m < n 上述结果依然成立.

如果上面的这个公式可以拆分为两次，就可以用来加密。

• 我们可以在终端使用python来验证一下：

M = 4, N = 15, φ(n) = 8, e = 3,
d ? 3d -1 = 8
d = (8k+1)/3 -> ( 3, 11)
这里我们可以取d = 11

终端使用python验证欧拉定理

上面验证知道，m,n不一定要，只需要m < n即可。

终端使用python来验证

从终端打印结构可以看出：n = 15 只要 m < n 也就是 m <= 14 无论是否是质数，公式：

比较第五步和第三步中红框部分

都成立。

• 然而科学家们一直停留在这个公式阶段，直到迪菲赫尔曼密钥交换出现，通过拆分这个公式实现。

3.5 迪菲赫尔曼密钥交换

• 实际场景来看下迪菲赫尔曼密钥交换过程如下图：

迪菲赫尔曼密钥交换-1

• 客户端先选一个随机数13 ，这个数除了客户端知道，没有其他任何人知道。
• 服务器选一个随机数15， 这个数字除了服务器端，没有任何知道。
• 这两个数字13，15分别只有客户端和服务器自己知道，不会在网络上传输，所以不会被泄密。
• 客户端用3作为根原， 3 的13次方 然后取模 17 （3^13mod 17 = 12），得到12，发给服务器端。
• 服务器端拿到12后，先将12保存起来，服务器端用同客户端一样的算法（3^15mod17 = 6）,得到数字6，发给客户端。
• 这样客户端和服务器端就完成了彼此的密钥交换。
• 然后客户端和服务器分别做如下一次运算：
• 客户端拿到服务器发过来的数字6，用同样的算法，（6^13mod17 = 10）, 服务器端用从客户端拿到的数字12，用同样的算法（12^ 15mod 17 = 10）同样也是得到10，这个10 就是客户端和服务器交换的秘钥。
• 这样网络上从来就没有传输过秘钥10，而客户端和服务器却通过同样的算法，计算两次就得到了密钥。

3.5.1 数学原理

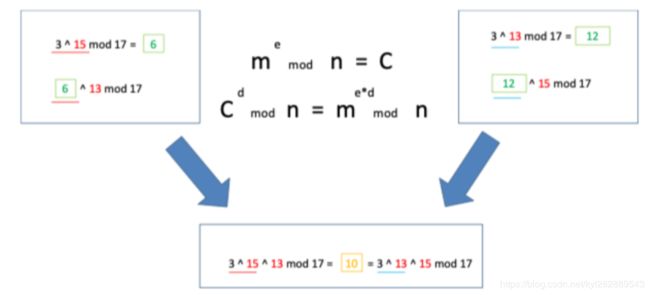
• 上面讲解的迪菲赫尔曼密钥交换的数学原理如下图：

  
  
  

  迪菲赫尔曼密钥交换-2
• 实际上客户端和服务器都做了两次运算，
• 客户端的两次运算：

1. 第一次是服务器端做的运算：3^15mod 17 = 6
2. 第二次是客户端自己拿到服务器端的6继续做的一次运算：6^13 mod17 = 10
3. 第二次运算的6 用第一次的3^{15替换就实际上得到：3}15^13 mod17 = 10

• 服务器端的两次运算：

1. 第一次是在客户端做的运算：3^13mod17 = 12
2. 第二次是拿到客户端的12继续做一次运算：12^15mod17 = 10
3. 第二次运算的12实际上是用3^13代替：313^15 mod 17 = 10

• 这样我们可以清楚的看到：客户端（3¹⁵13 mod17 = 10）= 服务器(3¹³15 mod 17 = 10)
• 那我们把上面的计算过程总结出来就是如下的公式：

原理1

上面的计算套用公式：
如上面服务器端的计算: m=3, e=13, n=17, C=12 （运算公式：3^13mod17 = 12）
实际上就是：m^e mod n = C
然后由于d = 15, （运算公式：12^15 mod 17 = 10）
实际上就是： C^d mod n = m ,由于 C = m ^ e mod n,可以得到 m ^ e ^ d mod n = m, 也就是：m ^ (ed) mod n = m
实际上就是对ed 进行了拆分，拆分成了两次运算。

• 结合我们刚刚第五步之后得出的

  
  
  

  第五步

• 拆分公式，可以用来加密，解密还原数据：

  
  
  

  加密解密公式

其中 d 是 e 相对于 φ(n) 的模反元素 , 因为 x = Φ(n) , 那么同样 , e 和 φ(n) 是互质关系

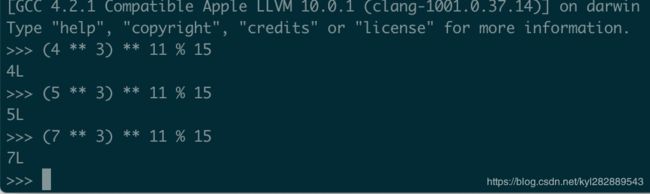
• 举例验证：例如: m = 3 , n = 15 , φ(n) = 8 , e = 3 , d = 11
  通过终端python3验证：

  
  
  

  加密解密验证

• 总结如图：
  

  迪菲赫尔曼密钥交换-2

3.7 RSA的诞生

• 由上面的迪菲赫尔曼密钥交换 和我们得出的公式：m ^ (e*d) mod n = m ,两者结合换算，可以得到加密和解密的公式：

1. 加密: m ^ e mod n = c, (c 加密的结果，m是明文， e和n就是公钥，d和n就是私钥)
2. 解密：c ^ d mod n = m

• 公式换算如下图：

  
  
  

  RSA原理

1. n 会非常大，长度一般为 1024 个二进制位。（目前人类已经分解的最大整数，232 个十进制位，768 个二进制位）
2. 由于需要求出 φ(n)，所以根据欧函数特点，最简单的方式 n 由两个质数相乘得到: 质数：p1、p2 . 那么
   Φ(n) = (p1 -1) * (p2 - 1)
3. 最终由 φ(n) 得到 e 和 d 。
   总共生成 6 个数字：p1、p2、n、φ(n)、e、d
   其中 n 和 e 组成公钥 .
   n 和 d 组成私钥 .
   m 为明文 .
   c为密文 .
4. 除了公钥用到了 n 和 e 其余的 4 个数字是不公开的。

3.8 RSA算法

• 只要满足d是e相对于Φ(n)的模反元素

• m小于n

  
  
  

  RSA算法

• 下面我们通过python来验证一下：

m ^ e mod n = c 加密
c ^ d mod n = m 解密
我们假设 n = 15 则 φ(n) = φ(15) = 8，
假设 e = 3
假设 d= 19
假设明文 m = 7
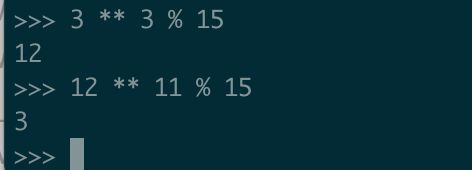
先来计算出加密：c = 7 ^ 3 mod 15 = 13
然后解密：13 ^ 19 mod 15 = 7

python验证RSA加密解密公式

• RSA算法的特点：

1. 总共生成 6 个数字：p1、p2、n、φ(n)、e、d
   其中 n 和 e 组成公钥 .
   n 和 d 组成私钥 .
   m 为明文 .
   c为密文 .
2. 除了公钥用到了 n 和 e 其余的 4 个数字是不公开的。
3. 黑客要破解实际上就是根据n, 去求φ(n)， 而当n比较大时，是很难算出φ(n)，φ(n)只能通过试错的方式去暴力破解（用因式分解方式）。
4. 要求出φ(n) 目前最大只能计算到232个十进制位，只是运算时间的问题，如果量子计算机真的出来了，因为量子计算理论上运算量是无穷大的，所以可以破解这个φ(n)，由于银行等很多大公司都是用的RSA加密方式，所以量子计算的问世，将会对密码学产生很大的影响。

3.9 终端演练RSA加密算法

• Mac的终端可以直接使用OpenSSL进行RSA的命令运行。

  
  
  

  Mac的终端可以直接使用OpenSSL
• OpenSSL使用RSA

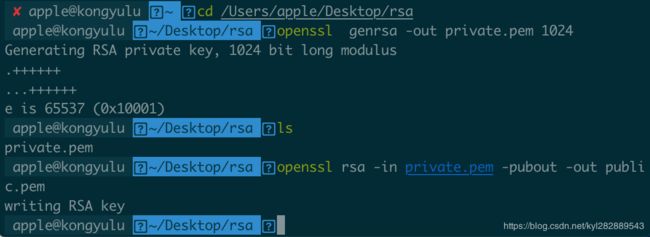
1. 生成RSA私钥，秘钥长度为1024bit
   终端输入命令：openssl genrsa -out private.pem 1024
   

   生成RSA私钥，秘钥长度为1024bit
2. 从私钥中提取公钥
   终端输入命令：openssl rsa -in private.pem -pubout -out public.pem
   

   从私钥中提取公钥

3. 通过上面两步分别已经生成了公钥，私钥文件

   
   
   

   生成公钥，私钥文件

4. 我们查看一下生成的公钥，私钥是什么东东

   
   
   

   私钥内容

5. 查看一下公钥内容：

   
   
   

   公钥内容
6. 实际上公钥，私钥都是经过base64加密的，我们接下来将私钥转换成明文查看：
   终端输入命令：openssl rsa -in private.pem -text -out private.txt
   
   

   转换base的私钥为明文

7. 我们查看一下私钥的明文：
   终端输入：cat private.txt

   
   
   

   查看私钥明文

3.9.1 openssl实现rsa加密 ,解密

• 打开终端，新建一个message.txt文件：vi message.txt

• 输入hello,保存

  
  
  

  新建一个message.txt
• 通过公钥进行加密：终端输入：

openssl rsautl -encrypt -in message.txt -inkey public.pem -pubin -out enc.txt

通过公钥进行加密

加密后的内容hello变成了乱码了。

• 通过私钥进行解密，终端输入：

penssl rsautl -decrypt -in enc.txt -inkey private.pem -out dec.txt

通过私钥进行解密

解密后在dec.txt输出了原来的明文hello

• 此外我们还可以用私钥进行加密，公钥进行解密。
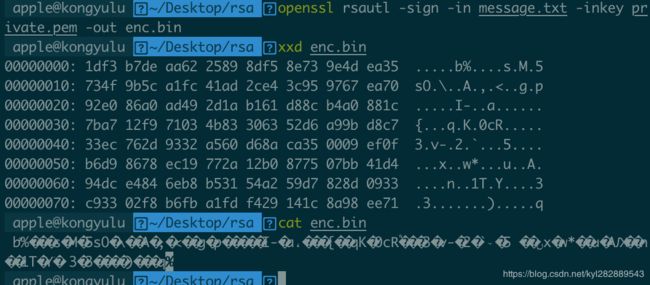
• 私钥通过sign进行私钥加密
• 终端输入命令：

penssl rsautl -sign -in message.txt -inkey private.pem -out enc.bin

私钥进行加密

• 然后我们用公钥进行解密，终端输入：

openssl rsautl -verify -in enc.bin -inkey public.pem -pubin -out dec.txt

解密到dec.txt ，我们可以看到解密后的明文也还原了hello

公钥进行解密

3.9.2 openssl 提取证书p12文件

• rsa 由于效率不高，不太适合大的数据加密，一般用来加密关键数据，如交换秘钥用rsa加密，rsa也经常用于加密hash值，也就是我们所说的签名。
• 在代码里面加密我们一般不会直接使用pem文件，一般要提前证书文件
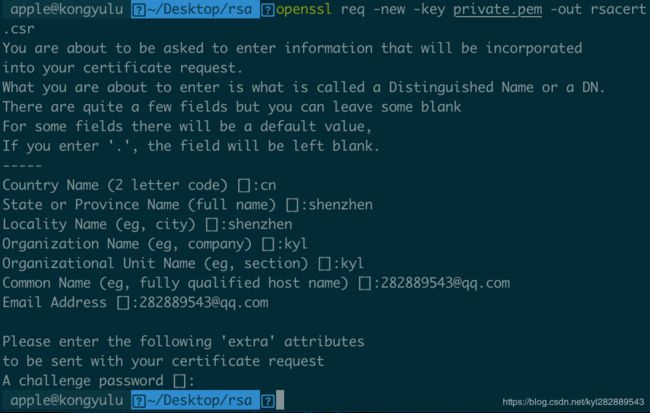
• 在终端输入：

openssl req -new -key private.pem -out rsacert.csr

会生成一个.csr文件
其中按提示输入一些信息，如邮箱，密码等

在这里插入图片描述

• csr文件实际上会去请求一个证书文件，向证书颁发机构颁发一个证书。
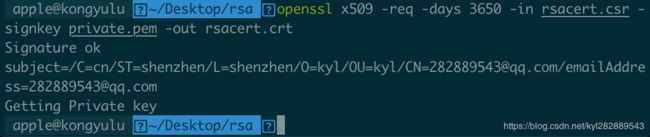
• 颁发证书终端命令：

openssl x509 -req -days 3650 -in rsacert.csr -signkey private.pem -out rsacert.crt

请求颁发证书文件

• 这样我们就得到了颁发的证书rsacert.crt文件：

  
  
  

  得到颁发的证书文件
• 这个颁发(官方认证，证书结构盖章的)的证书是要收费的，机构一般要收5千元一年，上面我们写的有效期是10年，意味着要交5万元，o my gad.
• 这个证书我们不会直接使用，还需要提前
• 终端输入命令：

openssl x509 -outform der -in rsacert.crt -out rsacert.der

提前证书文件der

• 提取到文件rsacert.der

  
  
  

  提取到文件rsacert.der
• 这个文件主要包含公钥和一些必要信息，后面我们就通过这个der生成一个p12文件，
• p12文件实际上就包含公钥和私钥。
• 接下来，我们到处p12文件。
• 终端输入命令

openssl pkcs12 -export -out p.p12 -inkey private.pem -in rsacert.crt

• 这个时候会提示我们输入密码，如下图：

  
  
  

  提前p12文件

• 输入密码后（需要确认两次密码）

  
  
  

  提前p12文件2

• 这样我们就提前到了p12文件

  
  
  

  这样我们就提前到了p12文件

• 实际上我们就可以用p.p12 和 rsacert.der进行加密和解密

  
  
  

  最终需要的两个文件

3.9.3 终端base64编码

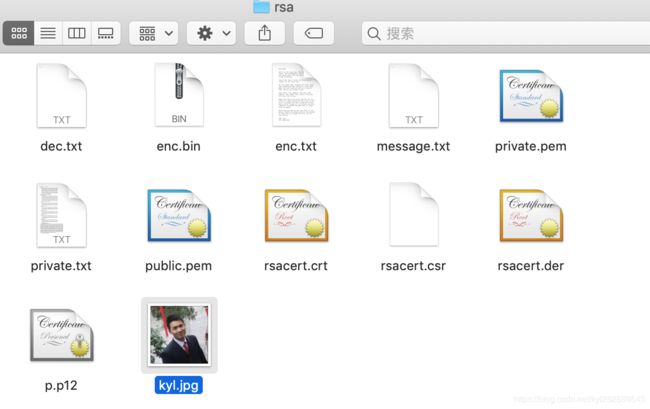
• 我们在rsa文件夹下面有一张kyl.jpg图片，现在通过终端进行base64编码

  
  
  

  图片base64编码

• 先终端cd 到rsa这个目录

  
  
  

  目录结构
• 终端输入编码命令：

base64 kyl.jpg -o pic.txt

base64编码图片

• 现在我们可以用终端进行base64解码：

base64 pic.txt -o 123.png -D

解码base64图片

解码后我们得到123.png图片

解码后我们得到123.png图片