前言
梯度下降法(Gradient Descent)是机器学习中最常用的优化方法之一,常用来求解目标函数的极值。
其基本原理非常简单:沿着目标函数梯度下降的方向搜索极小值(也可以沿着梯度上升的方向搜索极大值)。
但是如何调整搜索的步长(也叫学习率,Learning Rate)、如何加快收敛速度以及如何防止搜索时发生震荡却是一门值得深究的学问。接下来本文将分析第一个问题:学习率的大小对搜索过程的影响。全部源代码可在本人的GitHub:monitor1379中下载。
快速教程
前言啰嗦完了,接下来直接上干货:如何编写梯度下降法。代码运行环境为Python 2.7.11 + NumPy 1.11.0 + Matplotlib 1.5.1。
首先先假设现在我们需要求解目标函数func(x) = x * x的极小值,由于func是一个凸函数,因此它唯一的极小值同时也是它的最小值,其一阶导函数 为dfunc(x) = 2 * x。
import numpy as np
import matplotlib.pyplot as plt
# 目标函数:y=x^2
def func(x):
return np.square(x)
# 目标函数一阶导数:dy/dx=2*x
def dfunc(x):
return 2 * x
接下来编写梯度下降法函数:
# Gradient Descent
def GD(x_start, df, epochs, lr):
"""
梯度下降法。给定起始点与目标函数的一阶导函数,求在epochs次迭代中x的更新值
:param x_start: x的起始点
:param df: 目标函数的一阶导函数
:param epochs: 迭代周期
:param lr: 学习率
:return: x在每次迭代后的位置(包括起始点),长度为epochs+1
"""
xs = np.zeros(epochs+1)
x = x_start
xs[0] = x
for i in range(epochs):
dx = df(x)
# v表示x要改变的幅度
v = - dx * lr
x += v
xs[i+1] = x
return xs
需要注意的是参数df是一个函数指针,即需要传进我们的目标函数一阶导函数。
测试代码如下,假设起始搜索点为-5,迭代周期为5,学习率为0.3:
def demo0_GD():
x_start = -5
epochs = 5
lr = 0.3
x = GD(x_start, dfunc, epochs, lr=lr)
print x
# 输出:[-5. -2. -0.8 -0.32 -0.128 -0.0512]
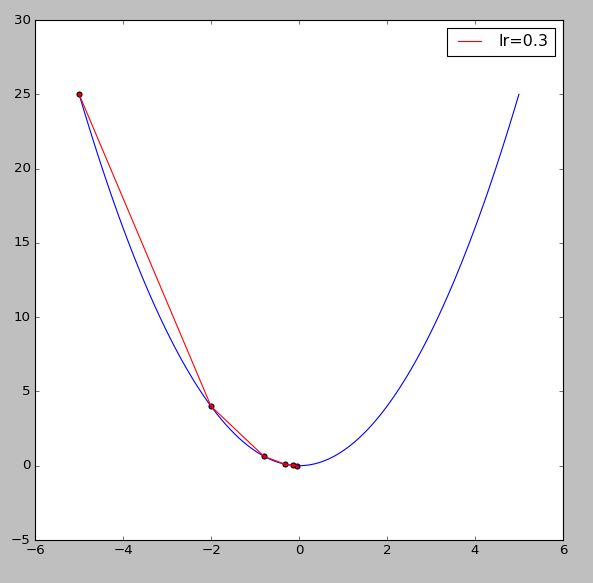
继续修改一下demo0_GD函数以更加直观地查看梯度下降法的搜索过程:
def demo0_GD():
"""演示如何使用梯度下降法GD()"""
line_x = np.linspace(-5, 5, 100)
line_y = func(line_x)
x_start = -5
epochs = 5
lr = 0.3
x = GD(x_start, dfunc, epochs, lr=lr)
color = 'r'
plt.plot(line_x, line_y, c='b')
plt.plot(x, func(x), c=color, label='lr={}'.format(lr))
plt.scatter(x, func(x), c=color, )
plt.legend()
plt.show()
从运行结果来看,当学习率为0.3的时候,迭代5个周期似乎便能得到蛮不错的结果了。
梯度下降法确实是求解非线性方程极值的利器之一,但是如果学习率没有调整好的话会发生什么样的事情呢?
学习率对梯度下降法的影响
在上节代码的基础上编写新的测试代码demo1_GD_lr,设置学习率分别为0.1、0.3与0.9:
def demo1_GD_lr():
# 函数图像
line_x = np.linspace(-5, 5, 100)
line_y = func(line_x)
plt.figure('Gradient Desent: Learning Rate')
x_start = -5
epochs = 5
lr = [0.1, 0.3, 0.9]
color = ['r', 'g', 'y']
size = np.ones(epochs+1) * 10
size[-1] = 70
for i in range(len(lr)):
x = GD(x_start, dfunc, epochs, lr=lr[i])
plt.subplot(1, 3, i+1)
plt.plot(line_x, line_y, c='b')
plt.plot(x, func(x), c=color[i], label='lr={}'.format(lr[i]))
plt.scatter(x, func(x), c=color[i])
plt.legend()
plt.show()
从下图输出结果可以看出两点,在迭代周期不变的情况下:
- 学习率较小时,收敛到正确结果的速度较慢。
- 学习率较大时,容易在搜索过程中发生震荡。
综上可以发现,学习率大小对梯度下降法的搜索过程起着非常大的影响,为了解决上述的两个问题,接下来的博客《【梯度下降法】二:冲量(momentum)的原理与Python实现》将讲解冲量(momentum)参数是如何在梯度下降法中起到加速收敛与减少震荡的作用。