概述
上一篇文章分析了一下基本的排序算法以及Java的实现,不过没有比较深入的去分析,因为对于O(n^2)的算法实现比较简单,但是对于O(nLogn)的算法本身有些复杂,所以就分为两篇文章来写。评价算法的标准有很多,时间复杂度,空间复杂度以及稳定性等等。下面从两个方面来对经典排序算法进行总结一下:
正文
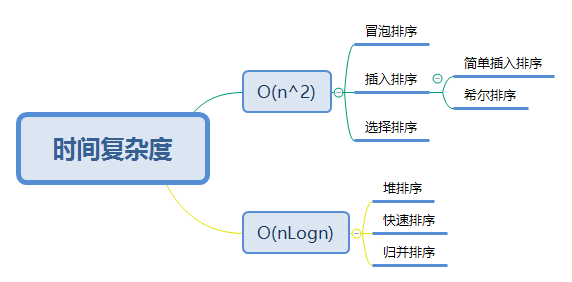
时间复杂度
经典排序算法的时间复杂度大致可以分为以上两种,下面来通过一个表格来看一下:
| 对比 | O(n^2) | O(nLogn) | 快的倍数 |
|---|---|---|---|
| n = 10 | 100 | 100 | 3 |
| n=100 | 10000 | 664 | 15 |
| n=1000 | 10^6 | 9966 | 100 |
| n=10000 | 10^8 | 132877 | 753 |
| n=100000 | 10^10 | 1660964 | 6020 |
当数据量比较小的时候,O(nLogn)的优势并不明显,当数据量越来越大的时候,优势才更加明显
先写一个测试的通用的工具类SortUtils
public class SortUtils {
// 生成有n个范围在[rangeL, rangeR]的数组
static Integer[] generateRandomArray(int n, int rangeL, int rangeR) {
assert rangeL <= rangeR;
Integer[] arr = new Integer[n];
for (int i = 0; i < n; i++)
arr[i] = (int) (Math.random() * (rangeR - rangeL + 1) + rangeL);
return arr;
}
// 生成一个有序数组, 之后随机交换swapTimes对
static Integer[] generateOrderedArray(int n, int swapTimes) {
Integer[] arr = new Integer[n];
for (int i = 0; i < n; i++)
arr[i] = i;
for (int i = 0; i < swapTimes; i++) {
int a = (int) (Math.random() * n);
int b = (int) (Math.random() * n);
int t = arr[a];
arr[a] = arr[b];
arr[b] = t;
}
return arr;
}
}
通过反射测试排序算法:
// 通过反射获取调用相应的方法
static void testSort(String sortClassName, Comparable[] arr) {
// 通过Java的反射机制,通过排序的类名,运行排序函数
try {
// 通过sortClassName获得排序函数的Class对象
Class sortClass = Class.forName(sortClassName);
// 通过排序函数的Class对象获得排序方法
Method sortMethod = sortClass.getMethod("sort", new Class[]{Comparable[].class});
// 排序参数只有一个,是可比较数组arr
Object[] params = new Object[]{arr};
long startTime = System.currentTimeMillis();
// 调用排序函数
sortMethod.invoke(null, params);
long endTime = System.currentTimeMillis();
System.out.println(sortClass.getSimpleName() + " : " + (endTime - startTime) + "ms");
} catch (Exception e) {
e.printStackTrace();
}
}
O(n^2)排序算法
编写测试方法
Integer[] arr1 = SortUtils.generateRandomArray(N, 0, 20000);
Integer[] arr2 = Arrays.copyOf(arr1, arr1.length);
Integer[] arr3 = Arrays.copyOf(arr1, arr1.length);
Integer[] arr4 = Arrays.copyOf(arr1, arr1.length);
SortUtils.testSlow("com.wustor.slow.SelectionSort", arr1);
SortUtils.testSlow("com.wustor.slow.InsertionSort", arr2);
SortUtils.testSlow("com.wustor.slow.BubbleSort", arr3);
SortUtils.testSlow("com.wustor.ShellSort", arr4);
测试随机数据
500条数据:
SelectionSort : 7ms
InsertionSort : 14ms
BubbleSort : 14ms
ShellSort : 0ms
1000条数据:
SelectionSort : 18ms
InsertionSort : 16ms
BubbleSort : 24ms
ShellSort : 1ms
5000条数据:
SelectionSort : 75ms
InsertionSort : 164ms
BubbleSort : 195ms
ShellSort : 9ms
20000条数据:
SelectionSort : 1265ms
InsertionSort : 1361ms
BubbleSort : 2999ms
ShellSort : 22ms
总结一下
| 随机数据 | 500条 | 1000条 | 5000条 | 20000条 |
|---|---|---|---|---|
| SelectionSort | 7ms | 18ms | 75ms | 1265ms |
| InsertionSort | 14ms | 16ms | 164ms | 1361ms |
| BubbleSort | 14ms | 24ms | 195ms | 2999ms |
| ShellSort | 0ms | 1ms | 9ms | 22ms |
测试有序数据
500条数据:
SelectionSort : 11ms
InsertionSort : 2ms
BubbleSort : 1ms
ShellSort : 3ms
1000条数据:
SelectionSort : 6ms
InsertionSort : 10ms
BubbleSort : 10ms
ShellSort : 1ms
5000条数据:
SelectionSort : 98ms
InsertionSort : 8ms
BubbleSort : 82ms
ShellSort : 3ms
20000条数据:
SelectionSort : 624ms
InsertionSort : 28ms
BubbleSort : 991ms
ShellSort : 20ms
总结一下
| 有序数据 | 500条 | 1000条 | 5000条 | 20000条 |
|---|---|---|---|---|
| SelectionSort | 11ms | 6ms | 98ms | 624ms |
| InsertionSort | 2ms | 10ms | 8ms | 28ms |
| BubbleSort | 1ms | 24ms | 82ms | 991ms |
| ShellSort | 3ms | 1ms | 3ms | 20ms |
通过对比可以发现,不管是测试有序还是无序的数据,希尔排序都是效率最高的。
O(nlogn)排序算法
编写测试方法
public static void main(String[] args) {
int T = 1000000;
int N = 20000;
// 比较 HeapSort、Shell Sort 和 Merge Sort 和 三种 Quick Sort 的性能效率
Integer[] arr1 = SortUtils.generateRandomArray(T, 0, N);
// Integer[] arr1 = SortUtils.generateOrderedArray(T, N);
Integer[] arr2 = Arrays.copyOf(arr1, arr1.length);
Integer[] arr3 = Arrays.copyOf(arr1, arr1.length);
Integer[] arr4 = Arrays.copyOf(arr1, arr1.length);
long time1 = SortUtils.testFast("com.wustor.ShellSort", arr1);
long time2 = SortUtils.testFast("com.wustor.fast.HeapSort", arr2);
long time3 = SortUtils.testFast("com.wustor.fast.MergeSort", arr3);
long time4 = SortUtils.testFast("com.wustor.fast.QuickSort", arr4);
System.out.println("Sorting " + N + " elements " + T + " times. Calculate theRun Time.");
System.out.println("Shell Sort Run Time: " + time1 + " ms");
System.out.println("Heap Sort Run Time: " + time2 + " ms");
System.out.println("Merge Sort Run Time: " + time3 + " ms");
System.out.println("Quick Sort Run Time: " + time4 + " ms");
}
测试随机数据
因为只有数据量涉及到几十万甚至上百万的时候,才能体体现出O(nlogn)的优势
10000条数据:
Shell Sort Run Time: 0 ms
Heap Sort Run Time: 0 ms
Merge Sort Run Time: 93 ms
Quick Sort Run Time: 0 ms
20000条数据:
Shell Sort Run Time: 16 ms
Heap Sort Run Time: 15 ms
Merge Sort Run Time: 0 ms
Quick Sort Run Time: 0 ms
100000条数据:
Shell Sort Run Time: 75 ms
Heap Sort Run Time: 44 ms
Merge Sort Run Time: 110 ms
Quick Sort Run Time: 62 ms
1000000条数据:
Shell Sort Run Time: 1062 ms
Heap Sort Run Time: 734 ms
Merge Sort Run Time: 281 ms
Quick Sort Run Time: 282 ms
测试随机数据
| 随机数据 | 10000条 | 20000条 | 100000条 | 1000000条 |
|---|---|---|---|---|
| Shell Sort | 0ms | 16ms | 75ms | 1062ms |
| Heap Sort | 0ms | 15ms | 44ms | 734ms |
| Merge Sort | 93ms | 0ms | 110ms | 281ms |
| Quick Sort | 0ms | 0ms | 62ms | 282ms |
测试有序数据
10000条数据:
Shell Sort Run Time: 0 ms
Heap Sort Run Time: 0 ms
Merge Sort Run Time: 16 ms
Quick Sort Run Time: 0 ms
20000条数据:
Shell Sort Run Time: 16 ms
Heap Sort Run Time: 0 ms
Merge Sort Run Time: 15 ms
Quick Sort Run Time: 16 ms
100000条数据:
Shell Sort Run Time: 77 ms
Heap Sort Run Time: 52 ms
Merge Sort Run Time: 62 ms
Quick Sort Run Time: 31 ms
1000000条数据:
Shell Sort Run Time: 1086 ms
Heap Sort Run Time: 606 ms
Merge Sort Run Time: 302 ms
Quick Sort Run Time: 257 ms
测试有序数据
| 有序数据 | 10000条 | 20000条 | 100000条 | 1000000条 |
|---|---|---|---|---|
| Shell Sort | 0ms | 16ms | 77ms | 1086ms |
| Heap Sort | 0ms | 0ms | 52ms | 606ms |
| Merge Sort | 16ms | 15ms | 62ms | 302ms |
| Quick Sort | 0ms | 16ms | 31ms | 282ms |
对比分析,发现快排不管是对于有序的还是无序的数组,排序效率都比较高。
稳定性
定义:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,ri=rj,且ri在rj之前,而在排序后的序列中,ri仍在rj之前,则称这种排序算法是稳定的;否则称为不稳定的。
根据这个定义来分析一下经典排序算法:
- 简单选择排序:由于需要交换元素的位置,所以有可能会破坏原来的顺序,比如说7571,第一次交换之后,两个7之间的顺序就调换了。不稳定
- 堆排序:在数据结构分析之二叉树中分析过二叉堆的数据结构,在堆排序之前需要将数组是生成一个二差堆,如果给定的二叉堆是数组是37556,那么进行生成二叉堆的时候层次遍历是35756,两个5相对顺序不变,但是取出最小值的时候,底部的元素进行上滤操作,后面的5会置顶,相对顺序被破坏。不稳定
- 直接插入排序:只有当后面的元素大于前面的元素的时候才会进行交换,所以不会破坏相同元素的顺序。稳定
- 希尔排序:分组的插入排序,虽然插入排序都是稳定的,但是每列之间的元素在排序之间会相互移动,这样就有可能导致相同元素之间的位置发生变化。不稳定
- 冒泡排序:第一个比第二个大,才进行交换,所以元素相同的元素之间不会进行交换,相对位置也就不会发生变化。稳定
- 快速排序:在分组的时候很容易把两个元素相同的位置进行交换,对于6225,分组的时候22之间的顺序会被打乱。不稳定
- 归并排序:分组进行递归,递归到最后,每一个数组都是有序的,合并的时候,也是从左到右的,相同的元素不会进行交换,所以可以保证稳定性。稳定
下面用图片总结一下
对比
| 算法 | 最大时间 | 平均时间 | 最小时间 | 辅助空间 | 稳定性 |
|---|---|---|---|---|---|
| 插入排序 | O(n^2) | O(n^2) | O(n) | O(1) | 稳定 |
| 冒泡排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 希尔排序 | O(n^(3/2)) | O(n^(3/2)) | O(n^(3/2)) | O(1) | 不稳定 |
| 快速排序 | O(n^2) | O(nlogn) | O(nlogn) | O(logn) | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
排序方法的选择
数据较小
有序
可采用直接插入排序。因为插入排序效率此时效率最高。
无序
采用直接插入排序或者直接选择排序
数据较大
快速排序在完全有序的情况下,会退化到O(n^2)级别,效率较低
有序
则应采用时间复杂度为 O(nLogn)的排序方法:堆排序或归并排序
无序
则应采用时间复杂度为 O(nLogn)的排序方法:快速排序、堆排序或归并排序
以上选择是在对排序算法稳定性没有要求的情况下进行选择的,如果需要排序稳定,则需要剔除不稳定的算法,在排序稳定的算法里面进行选择即可。
源码下载