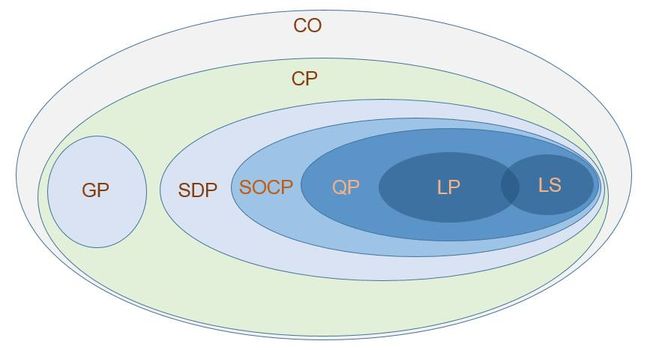
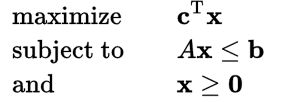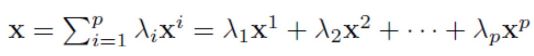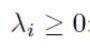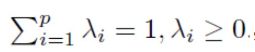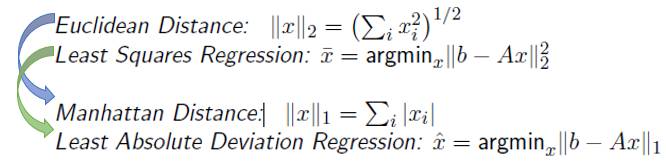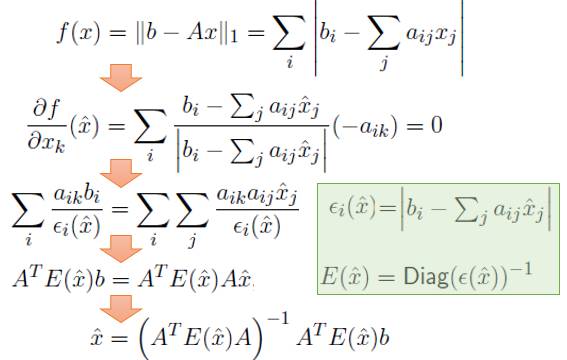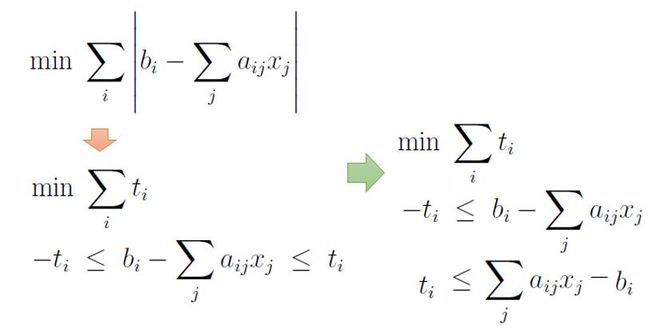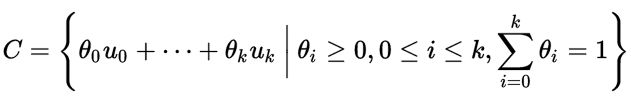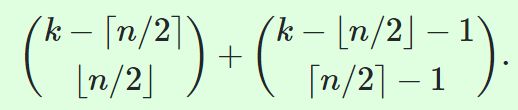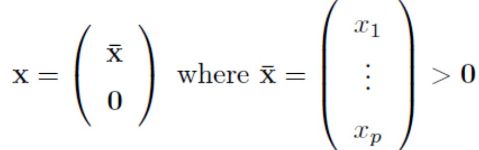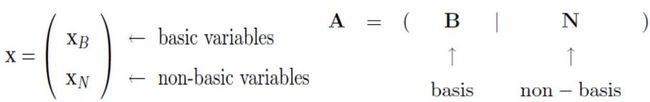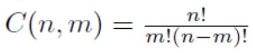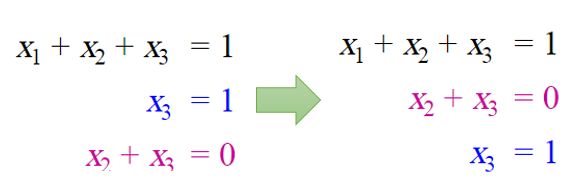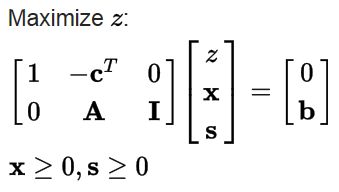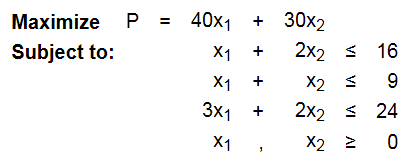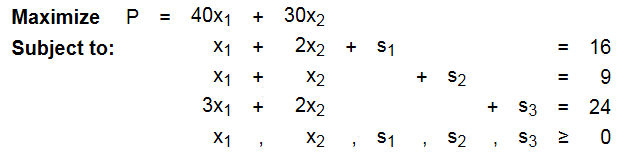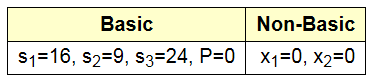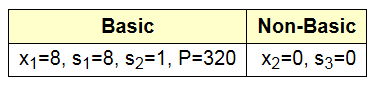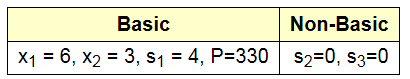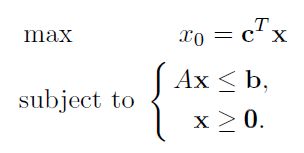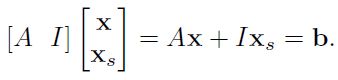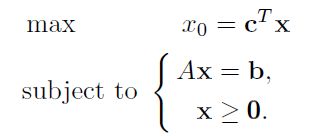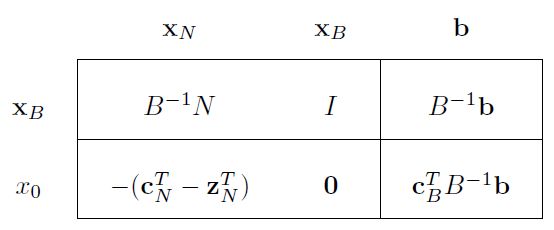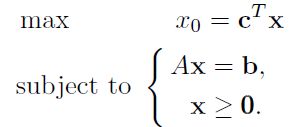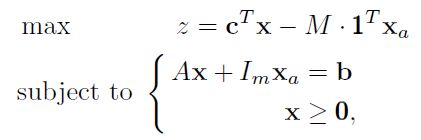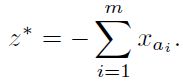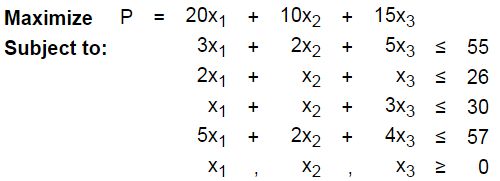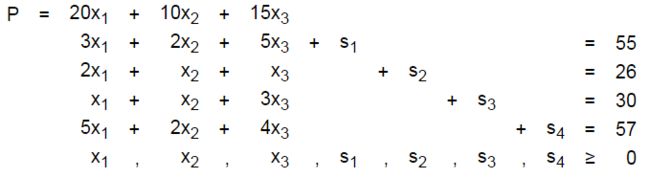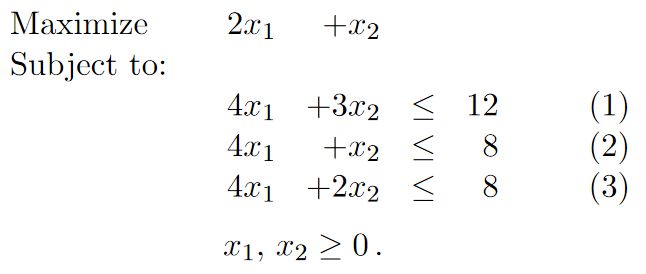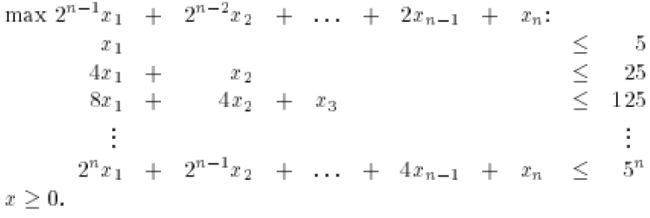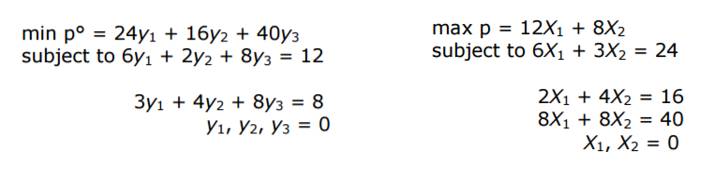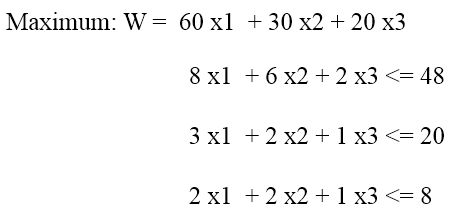一般来说凸优化(Convex Optimization, CO)中最一般的是锥规划 (Cone Programming, CP)问题, 前面我们介绍了最简单的是最小二乘(Least Square, LS)问题, 现在我们介绍一点线性规划(Linear Programming, LP)
引子
彼得堡学派是人类近代史的一个奇迹, 是由切比雪夫(ChebyShev)一手开创, 切比雪夫研究的领域包括, 数论、概率论、函数逼近论、积分学, 这些都在这个学派极大开花, 而切比雪夫之所以能成为这个开创者, 一个重要原因就是他从小精通法语, 并且大胆积极的和法国数学家沟通交流。 另外一个重要原因就是善于培养学生,马尔可夫、李亚普诺夫都是他的学生, 都是一等一的数学大师, 这绝不是偶然。这个学派对概率和各种不等式玩的出神入化, 对近代机器学习的发展影响巨大!
帕夫努季·利沃维奇·切比雪夫本人, 出身于贵族家庭.他的祖辈中有许多人立过战功. 父亲列夫·帕夫洛维奇·切比雪夫参加过抵抗拿破仑(Napoleon)入侵的卫国战争, 母亲阿格拉费娜·伊万诺夫娜·切比雪娃也出身名门,他们共生育了五男四女,切比雪夫排行第二.切比雪夫的法语就是来自母亲精心的教育! 题外话, 日本的一般妇女都会二门外语左右, 这对子女的教育都是极大的优势!
切比雪夫对数学的兴趣,来自阅读并思考了欧几里得(Euclid)《几何原本》(Elements)。 题外话, 现在各大中小学, 从来没有时间给学生阅读数学原著和思考, 整天重复做题, 还指望培养一流大数学家, 简直不可能。
有个年轻的犹太俄罗斯数学家Leonid Vitaliyevich Kantorovich, 受到了这个学派的极大影响, 在概率, 不等式, 数值逼近方法做出了极大贡献。 并且获得诺贝尔经济学奖。
Kantorovich对一般性线性规划进行了归纳,并且最先提出了解法。 从此线性规划最先走向了经济领域,走向了世界。
什么是LP, 线性规划
标准形式
LP正如其名,目标是求线性乘积的最值, 并且受到线性不等式的约束。标准形式如下:
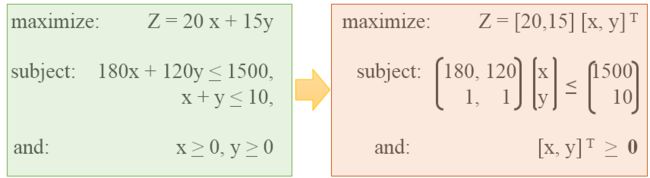
举个例子, 经过标准化就是上面我们形式了:
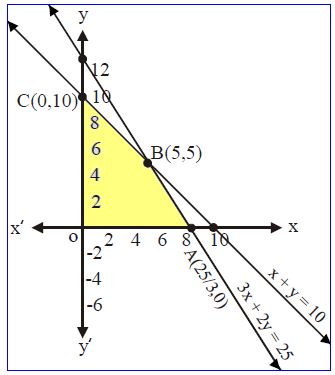
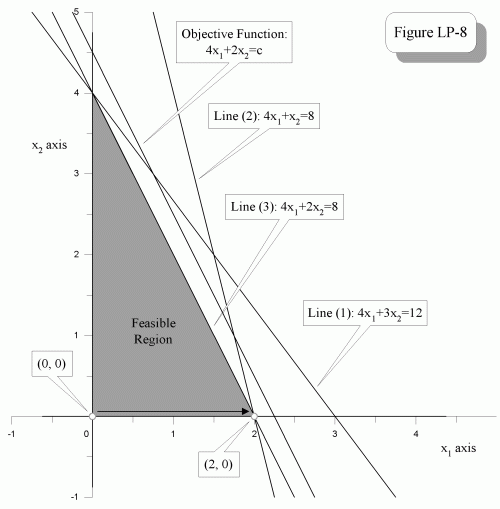
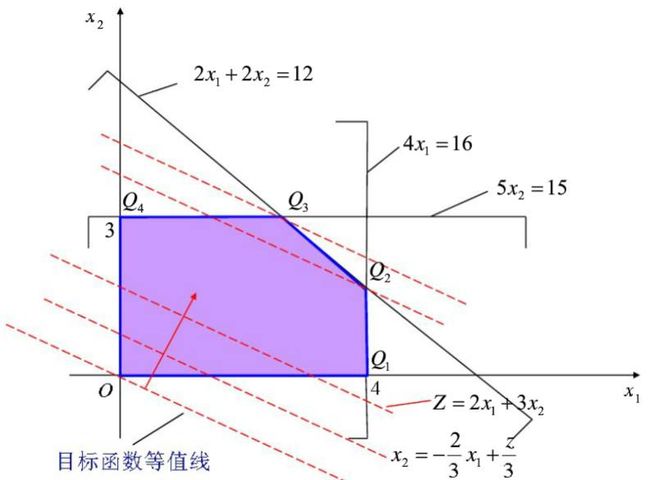
把上面的所有线性要求图形化, 根据不等式知道,定义域为黄色的凸区域:
图形化求解这个比较容易,因为目标公式是线性函数, 所以只要考虑凸区域的最值点, 又因为凸区域本身就是直线围起来的, 所以只要考虑角就行了
这样可以得到在x=5, y=5这个点, LP问题取到最大值。
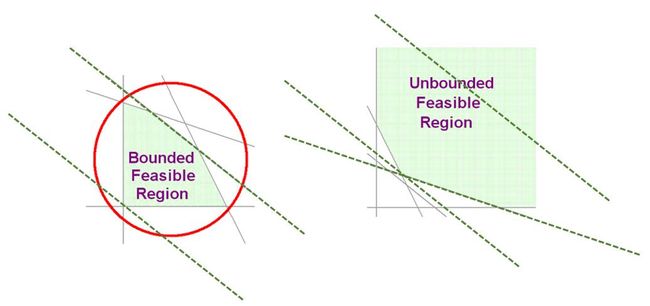
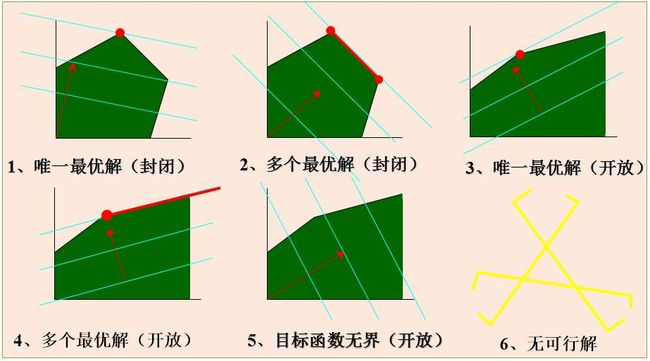
但是我们稍微讨论一下最优值的分布, 一般情况下, 不等式围成的区域有三种情况:
空集合(null set):这种情况天然没有最优解(optimum)。
有限可行区域: Bounded Feasible Region
有唯一解(unique optimal)
有无数解(multiple optimal)
无限可行区域: Unbounded Feasible Region
无最优解
有唯一解(unique optimal)
有无数解(multiple optimal)
顺便, 我们说明一下带权求和(weighted sum)的几何含义: 对于点积p个点和它们的系数的点积。
我们讨论三种限制情况:
1. 如果常量之和为1:
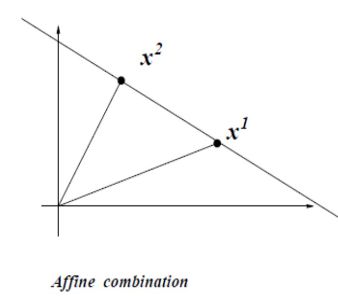
这是X被称为仿射求和(affine combination): 是两点直线上所有点
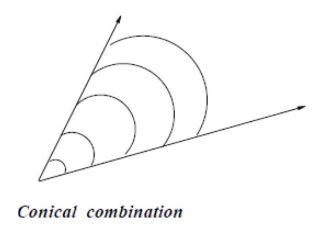
2. 如果所有常数为非负:
这是X被称为锥求和(conic combination):是两个点向量方向之间所有可能方向可能的向量。
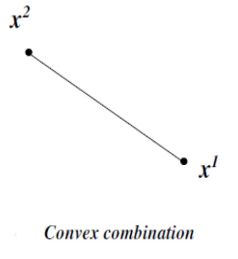
3. 如果同时满足affine combination 和 conic combination,
这时候被称为凸求和(convex combination):是两个点之间线段上所有点
有了凸求和的定义, 那么我们就可以通过凸求和来判断一个点是不是角:
角只能是自己和自己的凸求和,或者角不是任何其他两个点的凸求和。
如果一个点可以表示成两个点的凸求和, 那么这个点就不是角。
这样,我们给出了LP的一般定义,以及图形化解法。
几个经典问题
在LS问题里面, 我们把误差定义为欧式空间距离(Euclidean Distance), 如果我们换成曼哈顿距离(Manhattan Distance), 那么我们就得到Least Absolute Deviation Regression (LADR)。
利用Subgradient求导, 我们可以得到LS类似的结论:
通过简单的变换, 我们就能把LADR问题转换成LP问题了:
除了基于Manhattan距离的回归, 还有基于Chebyshev距离的回归, 他们都是典型的LP问题:
LP的几何意义
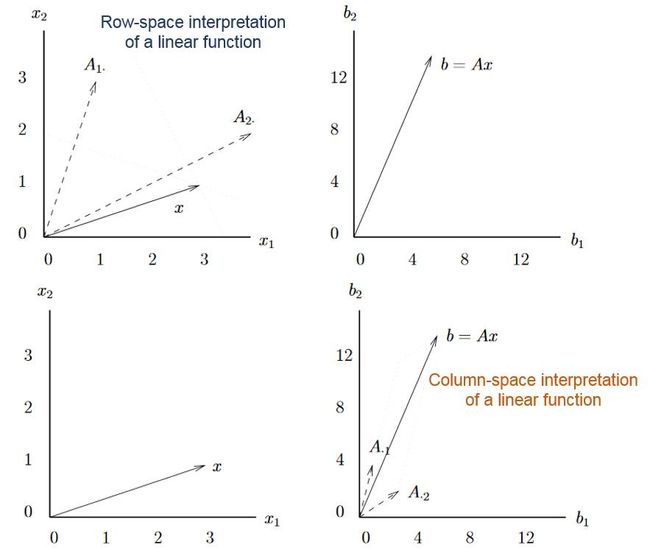
从矩阵空间看
LP的矩阵空间比较简单, 只有线性的乘法, 因此只有简单的矩阵空间的关系,意义不是很大。
从仿射空间看(affine space)
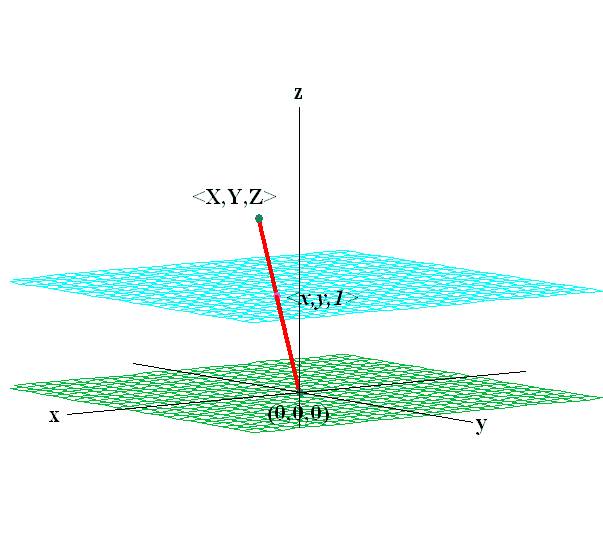
Affine space和前面的subspace最大的区别就是, Affine只保留了相对欧式距离关系。 举个例子, 下面图里有两层子区域, 在原点的可以构成suspace, 但是上层的不能构成一个subspace, 因为不能满足线性生成(span),包括线性组合和缩放,依然属于这个区域, 具体可以看“矩有四子”中子空间的定义。 但是这个区域依然保留着相对关系,是一个仿射空间。
为什么要有仿射空间呢?
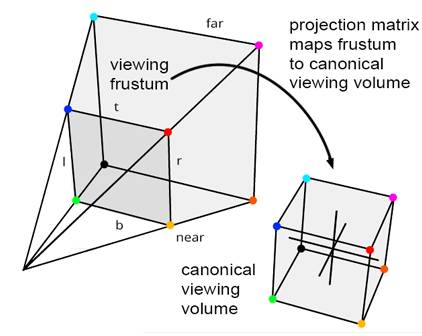
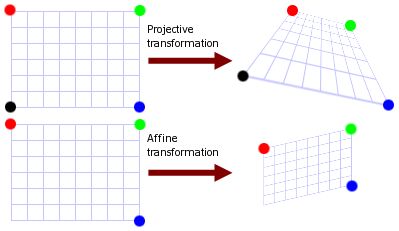
有了仿射空间的定义, 我们就可以对仿射空间进行变换。 否则只能在固定的投影空间(Projection)里面, 就需要对4个点都要计算, 因为我们要保留子空间的特性(绝对位置关系)。 但是在仿射空间里面, 我们只要保留相对位置空间, 所以只需要对3个点进行定位确定相对线性关系。
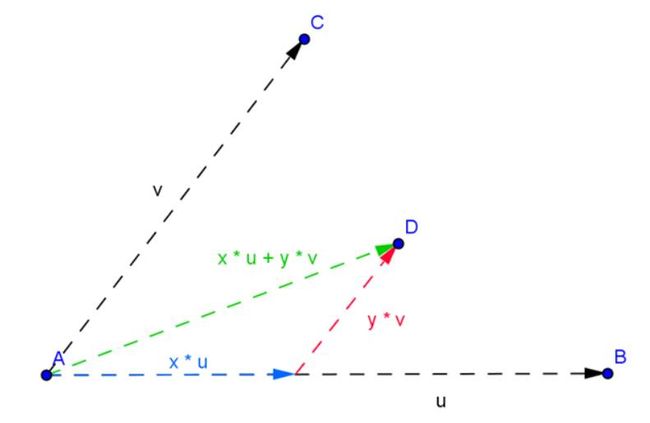
有了上面的了解, 我们再来看一个我们已经很常用的affine combination。 在下面的二维空间里面, 点D就是A, B, C三点之间的相对关系计算出来的点, 而不考虑A点自己的向量关系。
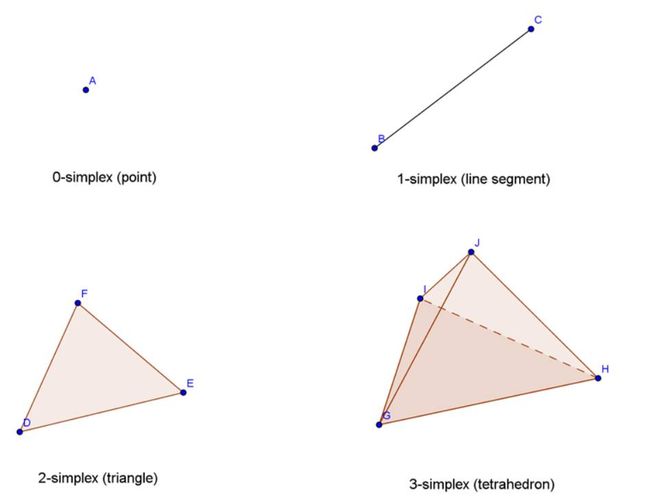
有了仿射空间, 我们在求LP问题的时候, 根据仿射空间和线性目标, 我们就知道, 极值点只能在仿射空间区域的角(Corner)取到, 这样就能构建单纯形Simplex区域来进行计算了。
Simplex就是通过空间点线性仿射连接(affine combination)构成的一个凸包区域。
LP概述
在Kantorovich提出线性规划的问题之后, 美国数学家Dantzig在1947年提出了单纯形算法(Simplex),Dantzig是来自波兰的美国数学家, 他的博士导师Jerzy Neyman相当牛, 是美国统计系(伯克利统计系)的第一个创建者。
之后,Fiacco 和 McCormick在60年代提出了早期的插值算法(interior-point methods, IPM), 到了70年代, 人们又提出了椭面法(ellipsoid method), 和一些subgradient methods。Ellipsoid 算法最大意义是首次提出多项式时间(polynomial-time)的算法,但是实际上这些方法都不如Simplex算法好用,Simplex算法被称为20世纪10大算法之一, 直到1984年来自印度的数学家Karmarkar提出了多项式时间(polynomial-time)的插值点算法(interior-point methods, IPM), 一下子改变了Simplex一家独大的状态。Karmarkar就是来自传说中的IIT的。
从此interior-point methods慢慢和Simplex算法并肩成为主流, 并且Simplex属于LP专业定制,很难扩展, 而Karmarkar的算法后来扩展到了非线性(nonlinear)问题中继续使用。
因此LP算法主流主要是Dantzig的Simplex和Karmarkar的IPM算法:
1994 Simplex Method:大部分中小规模问题超快,大规模问题不如IPM,偶尔情况很差。
1984Interior-point Method, IPM:大规模情况比较快,中小规模不如Simplex, 但是不会出现最坏情况。
Simplex 算法概述
Simplex思想
算法的思想比较直观,就是要在Simplex上从任意一个顶点(角)出发, 然后找到一条路,它的终点就是最优值点。 这个算法利用前面提到的最优点必然落在角上的结论。
为什么不能遍历所有的角(Corner)来找到最优点?
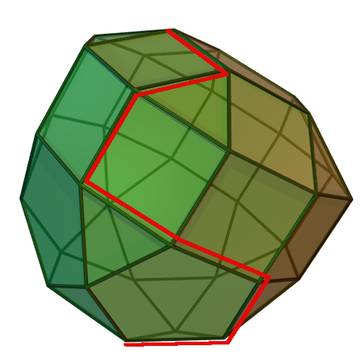
在n维度的空间里面,假设有k个切面围成一个多面体(polyhedron), 那么这个多面体最多有多少个角(Vertex)? 有如下结论:
这个结论可以通过在基本的Simplex上面添加切面来验证:
从上面的结论,我们可以知道, 这是随着k的增长指数增长的值。 所以, 根据LP的特征, 每个不等式就是一个切面, 然后把可能区域(feasible domain)围成一个凸的多面体, 而最优点一定在角上, 但是遍历所有角(Vertex)的数目是根不等式和维度个数而指数增长的, 是不可以取的策略。
在LP中, 角的数学上如何表达的?
假设角的集合为P,并且满足如下条件:
那么如果X是角点, 对A有什么要求(什么情况下是交点是角)?
为了不失一般性, 把x向量中,零向量部分分开表示。
在这种情况下, 我们把A也进行拆分成前p列为
。 那么:
那么X是角(Extreme Point)的要求是,对应的
矩阵是満秩的,或者矩阵的所有列是线性独立的(linearly independent)。
采用反证法, 证明如下:
已经知道角点X,要求
矩阵満秩, 那么満秩是不是一定是角点呢?同样反证法, 我们只要证明非角点一定不满秩就好了。
所以, 在Simplex算法中从一个角点跳到一个相邻的角点, 都必须满足非零部分对应的列是相互独立的(矩阵是満秩的)。
为了更好表示, 我们引入basis 和 non-basis来进行划分:
这样, 我们首先得找一个基本解(basic solution, bs), 让它满足
。 如果更进一步, 还能找到
。 那么我就找到一个基本可行解了(basic feasible solution, bfs),也就是说找到一个角了。
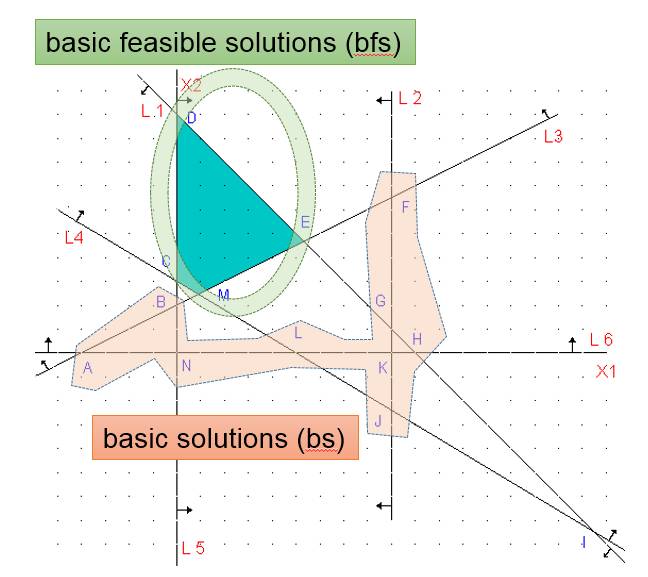
从下面图上可以直观的看到基本解 和基本可行解的差别了, 可行基本解使我们想要的凸多面体的角(CDEM), 而基本解还包含其多面体区域外的角。 另外(BTW),可行解(Feasible Solutions, fs)就是凸多面体内部区域(四边形CDEM和内部)。
有了上面角的数学表达形式这个结论, 我们很容易得到:
1. 如果A不是満秩(Full Rank)的, 那么就没有角, 那么就无解了。
2. 角的个数小于从列数(n)里面选出行数(m)个列的可能性。
虽然前面我们已经给出了更为精确的结论, 但是它的由来并不清楚, 而这里我们很容易推导出一个上限(bfs是bs的一个子集, bfs数量小于bs数量)。
邻居顶点是如何表示的?
有了上面的结论, 我们在来看一下如何通过矩阵来表示邻居顶点?
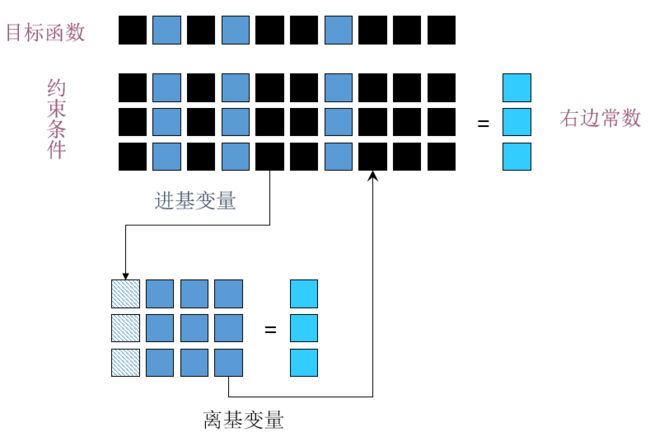
既然是邻居, 那么就是要共享大部分限制条件,最多只有一个限制条件不一致。 那么在矩阵里面, 就是要两个基集合(basic set)只有一个列不一样。
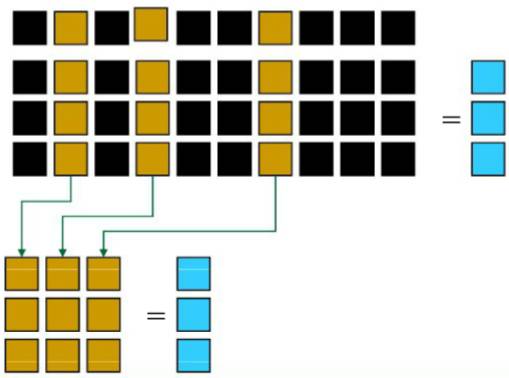
在这样的情况下, 从一个点移到另外一个邻居点就是选择一个新的非基点(non-basic)加入到基集合里面来, 同时从基里面选择原有的一个列放回, 如下图所示:
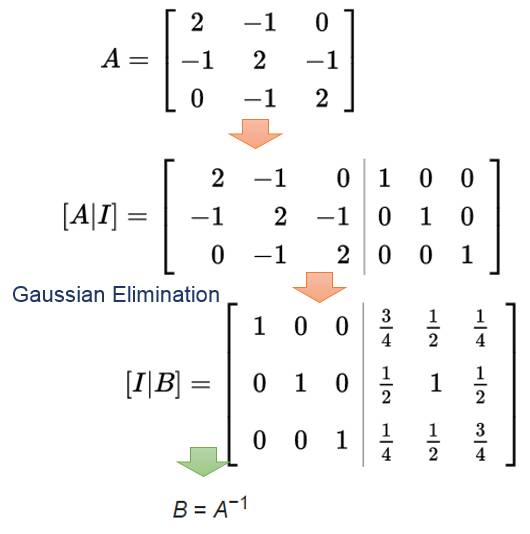
那么如何通过矩阵做到这一点呢? 就要通过高斯消去法(Gaussian Elimination, GE)。 举个极端的例子, 大家还记通过GE来求矩阵逆么?
我们会看到整个basis从联合矩阵右边移到左边, 然后就求解到了逆矩阵。
注意, 高斯消去法(GE)应用到计算机求解的时候经常会出现round-off error,或者divide by zero, 所以会每次选择pivot点进行操作。Pivot点选择也很简单就是把一列上最大值的行换到对应位置, 避免除以0或者小的数导致误差。
为什么需要松弛形式(slack form)?
前面我们讨论过, 顶点的形式要满足:
但是标准形式下面, 并不满足这两个条件。 因此Simplex这个算法利用的并不是LP的标准形式, 而是松弛形式(slack form )或者说增大形式(Augmented form), 这个形式就是通过引入松弛变量(slack), 来把矩阵乘法的不等式变成等式。 然后所有定义域变量都放到第一象限。 从而满足我们先前设定的角的简单形式。
Simplex算法的怎么设定优化目标的?
有了松弛形式之后,就是求解目标是什么?
Simplex 的目标就是基于等式, 在一个象限里面化解到一个目标表达式:
Z + c1 * x1 + c2 * x2 + c3 * x3 = b
等价于:
Z = b - c1 * x1 - c2 * x2 - c3 * x3
使得c1, c2, c3...的符号相同。
由于 X, Y, Z >= 0。 因此:
Z取最小值: 要求c1, c2, c3 <0,Z和x1, x2, x3单调性一致,x1=x2=x3=0的时候是最小值
Z取最大值: 要求c1, c2, c3 >0,Z和x1, x2, x3单调性相反,x1=x2=x3=0的时候是最小值
有了目标了, 那么求解方式是什么?
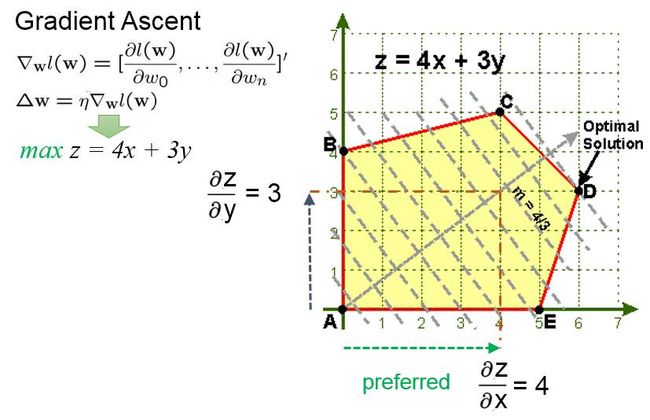
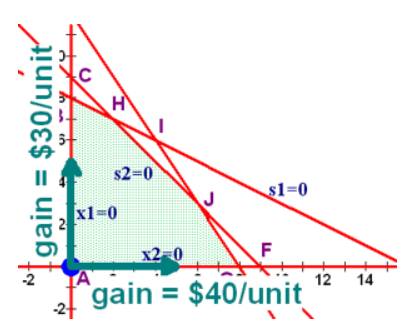
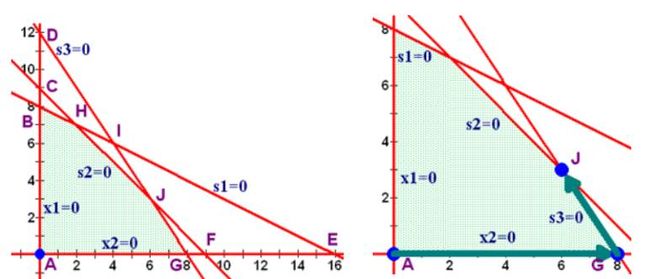
首先我们图示化来看一下, 从一个点到最优点(optimum)理想的路径的启发。 例如下图, 最理想的情况应该吧把直线Z=4x+3y,沿着梯度上升(Gradient ascent)的方向平移, 一直移到D点, 因为D和直线仅有一个交点了, 这种情况下Z取到最大值。
但是Simplex算法是从角集合之间进行移动的。 假如, 目前在A点,A点是一个基本可行点(bfs), 因为A点是角,所以是基本点(bs), 另外,A点在黄色区域内,所以是可行点(feasible solution)。 A点又两个邻居, B和E点。 那么B点和E点哪个更好呢?
根据前面最优的梯度上升的路径, 其实我们应该选择和梯度上升更为一致的方向。 那么B和E点的方向, 哪个方向更为和梯度方向一致呢? 我们可以把梯度分解到X轴和Y轴, 看到梯度在X轴上的分量是4,而在Y轴上的分量是3, 那么可以确定沿着X轴更为合适, 因为梯度在这个方向上投影更大, 之间的夹角更小,更为一致。
如果我们再把梯度的分量对应到等式z=4x+3y的系数, 就知道4是x的系数(coefficient), 而3是y的系数。 所以直观上来说, 我们要选系数更大的方向。
根据前面讲述的利用高斯消去法(GE)来进行从一个bfs点, 移到邻居的bfs点。 这时候, 也要选择pivot列进行操作。 前面我们提到, 只要想办法从basic 和non-baisc set 里面替换任意一列,就是变换到邻居了。 这里我们又加上, 要选择最大系数的方向操作。 因此pivot列就要选择系数最大的列优先进行GE操作。
如何选择Pivot点进行高斯消去法来交换basic列?
前面我们已经讲述了基本思想, 这里我们举个例子来进行说明:
对于标准的LP算法, 求如下最大值:
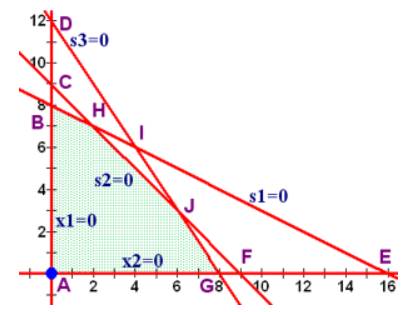
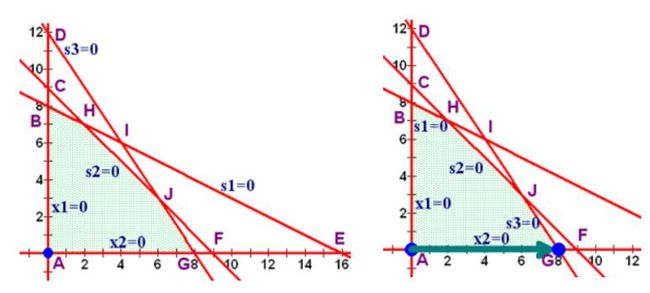
对应的图如下,所示:
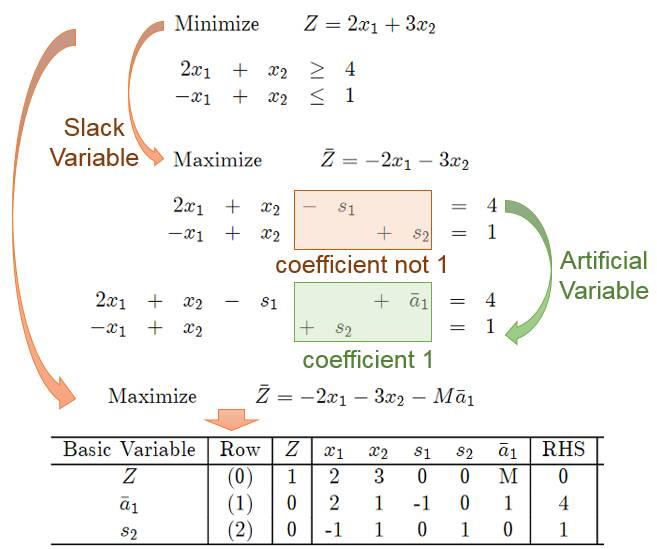
首先, 我们引入Slack变量, 换成Slack形式:
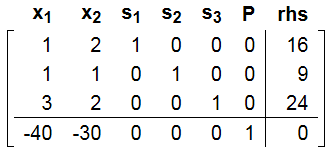
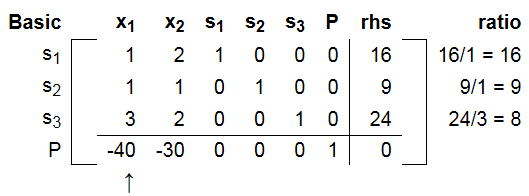
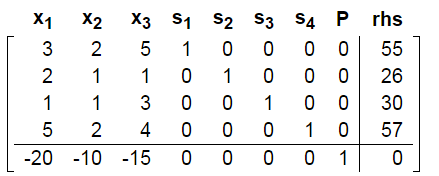
这样我们得到对应的Ax = b,x > 0的矩阵形式:
(注意: 目标公式化成了-40 x1 - 30 x2 + P = 0)
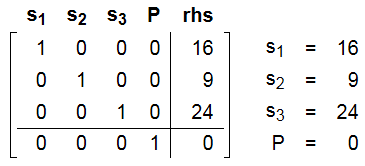
根据前面的矩阵基的理论, 很容易把slack变量对应的列选出来作为基:
在这种情况下, 很容易设定non-basic变量为0, 然后basic 变量就是b值。
我们发现这时候对应的是坐标0点, 图上A点。
根据我们之前讲述的理解, 我们应该往系数最大的x1轴(x2=0)的方向移动, 因此我们找到对应列, 为pivot列。
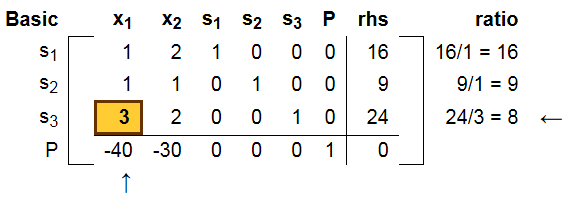
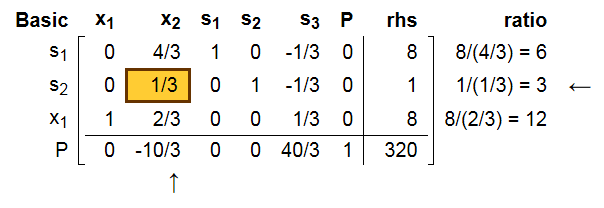
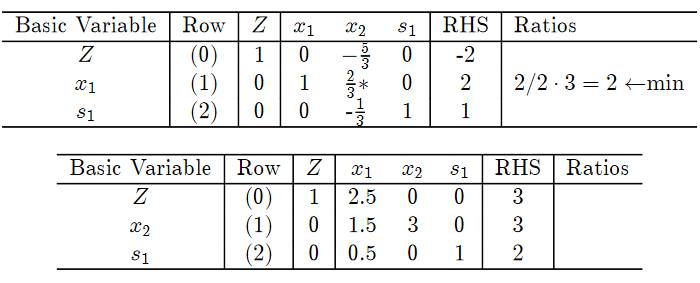
选择x1轴对应的列为pivot列, 如下图, pivot列是P行里面除了P列之外的最小的列(取了负号的最大系数)。
那么选择哪一行进行操作了呢? 根据高斯消去法里面Pivot行的思想, 我们应该选择pivot列里面最大值的行进行操作, 但是, 这里不是, 这里是选择正的 rhs / s 最小的行进行操作(等价于把rhs全部变成1, 然后每行除以b之后,对应的最大值的行)。如下图所示, 我们选择了24/3最小的行, 或者说选择了3/24最大列,依然符合pivot的思想。 当然这只是从pivot思想出发的阐述, 具体后面会说明为什么要选择正的值的最小pivot ratio。
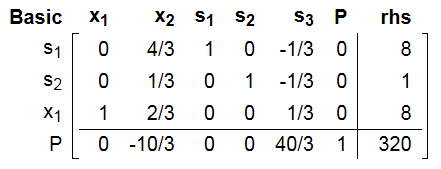
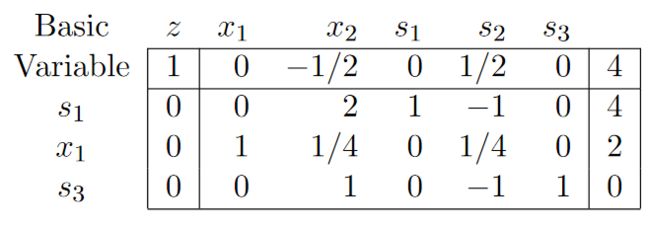
通过高斯消去(GE)之后, 得到如下:
这样, 我们得到了新的基集合和非基集合, 我们看到是对应的x2=0和s3=0的直线的交点:
而这个点就是我们要找的G点:
如果继续这个过程, 我们就会再找到x2是最大系数方向, s2是pivot选择的行:
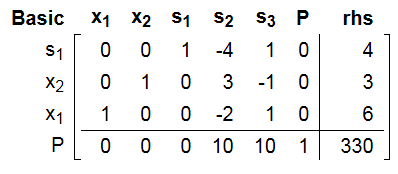
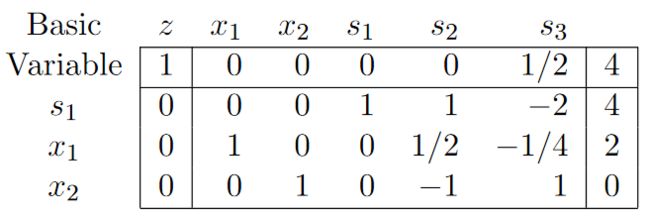
进行GE后,我们得到如下:
对应的新的基和非基集合是:
所以找到了s2=0和s3=0的交点:
这时候我们再来看P对应的行, 里面所有系数全部同号了, 而且全部是正号, 根据我们前面讲述的结论, 我们找到了最大值。
为什么Pivot行要选择pivot ratio最小的行?
前面我们直观的简单描述了pivot行的选择, 但是似乎不是强制的, 其实pivot行的选择是强制的。
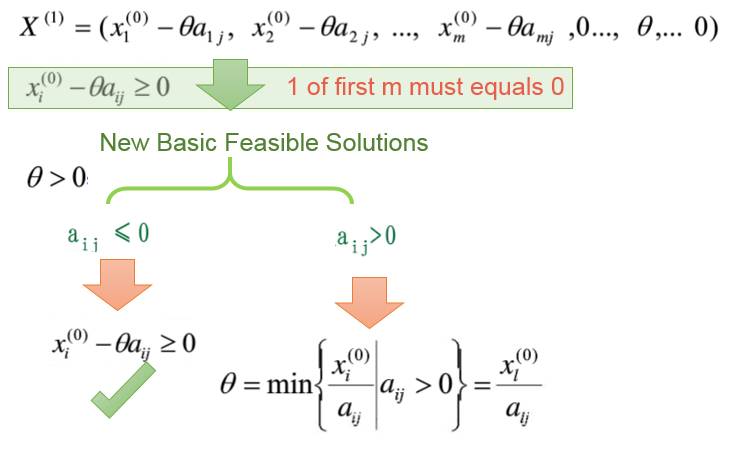
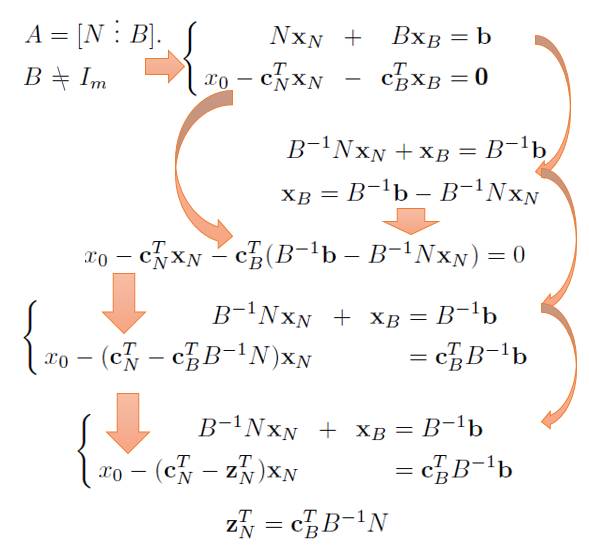
假设根据松弛变量扩展, 我们有如下结果, 然后我们改写一下, 把单位矩阵放到前面去:
假设我们选择了某一列,第j列, 那么我们很容易得到如下一组新的basic solution:
但是要使得这组basic solution成立就要求所有的X的分量全部大于等于0. 但是要使得basic feasible solution成立, 那么就要求前m个分量中至少有一个等于0.
在这种要求下, 讨论aij的大小, 如果aij<=0情况, 那么天然就有新的x>=0, 然是如果aij > 0的情况发生, 那么就要求theta的取值是最小pivot比值。
所以, 我们要求取theta为对b列和pj列的所有比值的最小值(必须正数)。
这就是为什么我们一旦选择了pivot列以后, 我们要选择pivot行为pivot ratio最小那一行做基值求解。
Simplex 算法详解
算法流程图
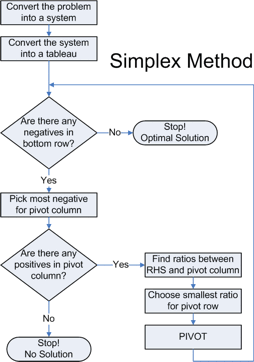
我们把上面流程总结一下,就是Simplex算法的流程了:
Simplex 如何限定到只关注基本可行解(bfs)?
前面我讲了, Simplex算法是从一个bfs,找到相邻的更优的bfs,直到相邻点里面没有更优的bfs了。 那么问题来了。如何找到第一个bfs?
如果是标准形式, 通过引入Slack变量:
那么对应的原点的bfs就是直观上可以应用的第1个:
要注意这里bi >= 0 否则, 解在第一象限就不成了。
从而得到:
如果直接就是增强模式:
通过一系列GE化解:
我们也可以得到一个带有单位阵的初始化矩阵:
这样如果令上面这个矩阵的non-basic变量全部为0那么有:
前面我们对bi >= 0 的情况进行了说明:
对于存在 bi < 0 的情况怎么办呢?
有两种方法可以做到这一点:
1.Big M Method,BMM,大M方法: 本质和下面TPM一样,但是初始化M是个问题。过大的M可能会导致计算中的error of round off, 小了, M会失效。
2.Two-Phase Method,TPM,两阶段法: 理论上更完美。
大M方法
由于slack变量能够平衡不等式小的一边, 如果 b<0, 虽然依然能将不等式化解成等式, 但是直接取slack变量为基的话, 那么slack variable = b < 0就不是基础可行解了。 我们知道一旦取得等式后, 我们就能让转换成所有b>0, 只是这时候slack变量系数就不是1了,不是天然基了。
因此大M方法,就是硬生生给b凑一个天然基变量, 但是这样又会破坏等式, 因此要这个变量必须等于0。 这样就要求优化目标中进行改写,使得取得最优值的时候,这个变量必须等于0.
在添加slack变量后始终能够做到让b > 0:
但是A = [ B | I ]不在成立了, 因此这时候利用大M办法继续添加变量。
这样我们能够得到[ A | I ], 这样就很容易得到一个bfs解作为Simplex算法的出发点。 但是我们看到 目标 Z 变了, 通过配置一个较大的M使得Xa = 0 的时候才是最大的。
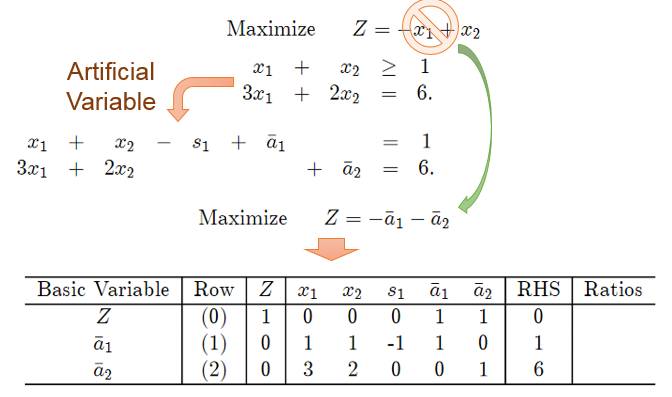
下面我们举个例子,详细说明:
这样就快要利用Simplex步骤求解了:
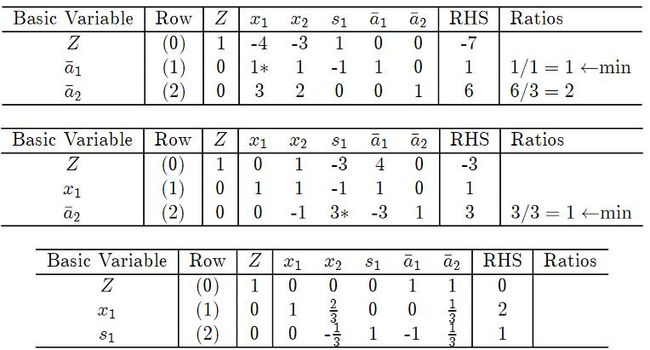
首先, 我们把目标公式里面的artificial variable的系数变成0. 然后利用Simplex进行选择pivot column和pivot row:
在GE之后得到如下:
这样我们就得到一组 bfs了:
所以我们只要利用artificial variable, 然后通过GE,找到置换后的一组bfs就是大M方法的思路。
但是大M方法由于取的M过大, 很容易导致round-off error问题, 尤其在计算机实现的时候。
两阶段法
我们知道, 本质上, 找到1组bfs只需要找到一个顶点, 因此跟目标公式没什么关系, 因此, Two Phase Method就是利用最简化的目标公式来找一个基本可行解。 这样,第一阶段, 通过如下目标公式找到一个bfs解。
第二阶段,利用找到的一组bfs, 通过Simplex算法求解目标。
举个例子, 如下直接替换原来的目标求解bfs:
第一阶段:
这样通过Simplex算法:
我们得到了一组non-basic variable(NBV)和basic variable(BV)
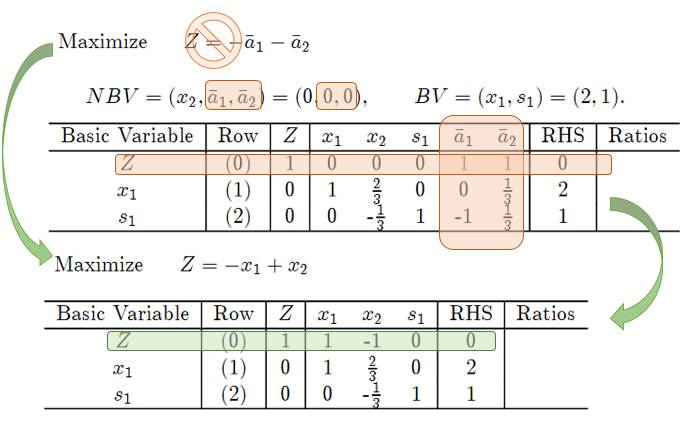
第二阶段:
这样对于原来的表达式, 我们得到一组解, 我们替换目标公式, 然后除去artificial variable(= 0), 得到如下公式:
然后再计算Simplex结果:
这我们求解到了最优解:
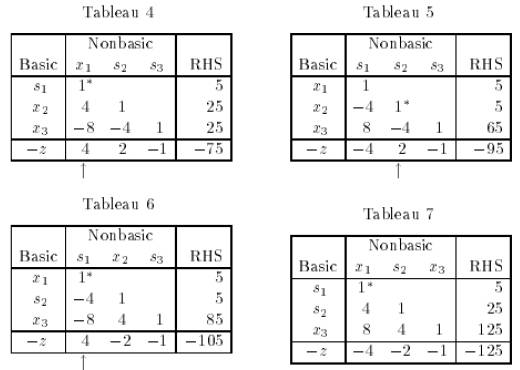
Simplex 算法举列
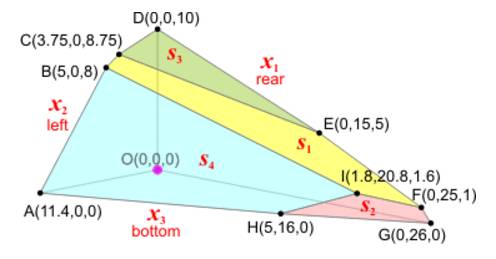
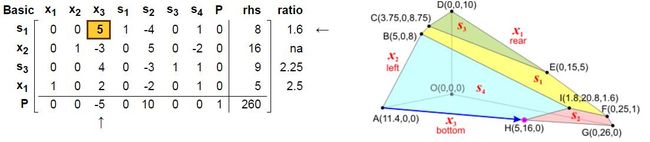
举个3维例子, 下面是一个最大值的例子:
1. 在不等号小的一边加入松弛变量(slack variable), 这样等式成立的时候, slack 变量必须在在第一象限(>= 0)。
2. 同时把目标P也引入等式左边。
3. 获得系数矩阵(Tableau)
对应的basic变量
根据non-basic变量为0,找到fbs点为原点。
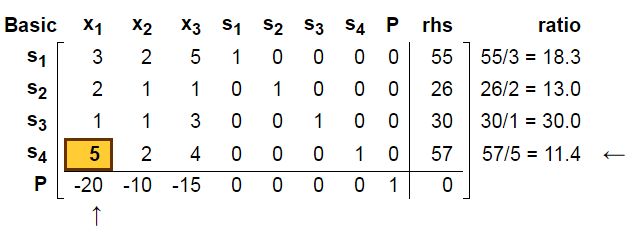
4. 找到初始的bfs点后, 因为是求最大值,根据前面的总结, 如何把上面系数矩阵的最后一行(目标行), 除了P之外参数全部变成正数。 所以开始循环向最优点移动:
GE处理完后得到新的矩阵
可以看到新找到A点, s4=0成立。
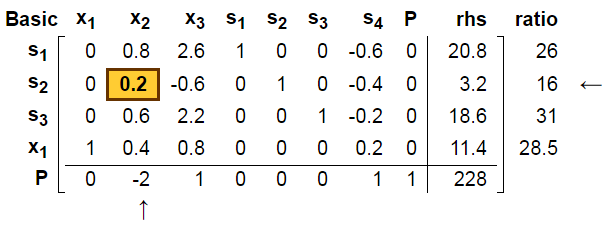
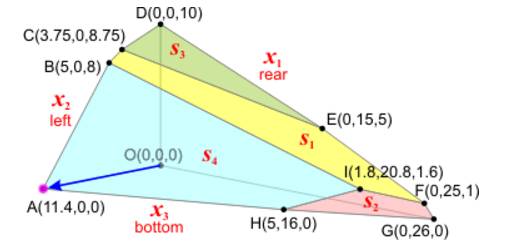
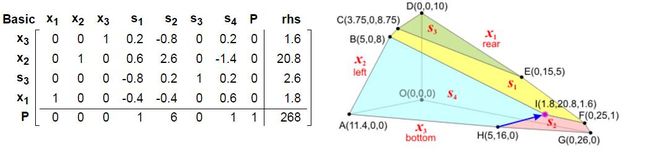
5. 继续我们找到了H点:
以及s2点:
6. 这时候所有的P值全部不小于零了, 因此找到最优值
Simplex 一个边界情况
原始的Simplex 算法对于有些情况可能不能处理的很好, 譬如下面这种情况, 存在算法退化(Degeneracy)的情况。
上面三个条件, 对应的图形如下, 我们可以看到三个条件围成的区域和如果去掉条件(1)(2)之后的情况一致。
在添加松弛变量后, 得到如下矩阵。
在执行了一次Simplex操作后, 从坐标原点走到了三角形的一个角。 这时候我们发现对应的basic变量存在为0的情况 (s3 = 0)。
在这种情况下,s3由于是basic变量, 但是因为b为0,所以也为0。 这时候s3被称为退化基变量。 这是再进行一次Simplex算法, 选择x2列第三行。
但是如果按照之前的Pivot ratio取大于0的最小比例, 这时候就会选择第2列,第1行。 这样操作后就会带来退化和循环的问题。 从多面体的图上看, 造成退化的主要原因就是有一些冗余直线经过角, 但是却不限界多面体区域。
对于退化的解决, 重要的思想是要尽量保持严格单调(strictly monotone),
这里就不细说, 更多细节可以参考:
1.Brand’s rule: 一个排序(order)的进入和出来的规则
2.Lexicographic rule(1955):
Simplex 算法局限性
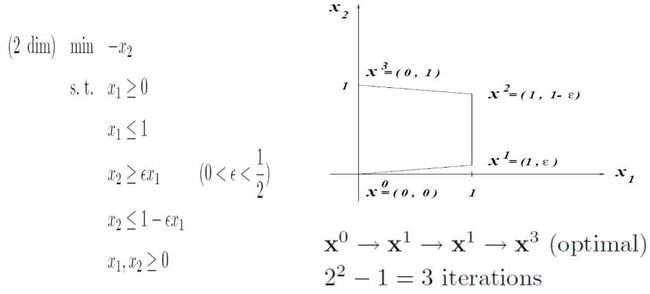
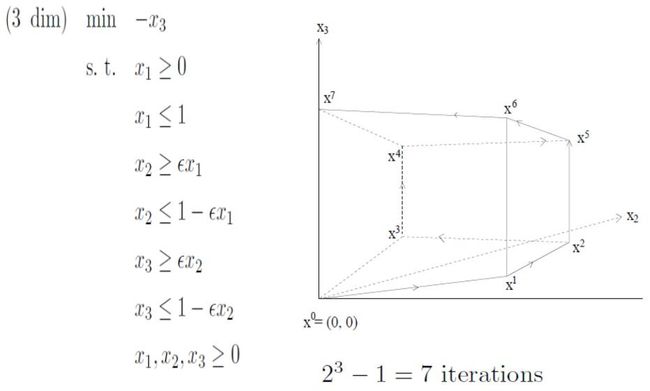
Klee-Minty在1972年给出了一个Simplex算法需要遍历所有点的例子:
这个例子的2维情况如下:
3维度情况如下:
这个图被称为Klee-Minty斜方体
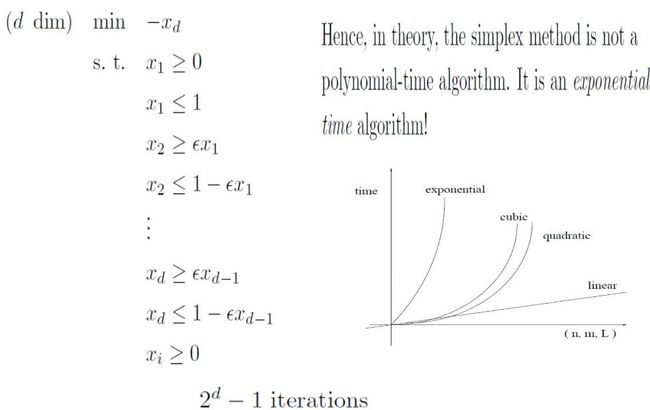
n 维的情况:
假如我们进一步把类似形式更具体化位矩阵表示2/5 < 1/2:
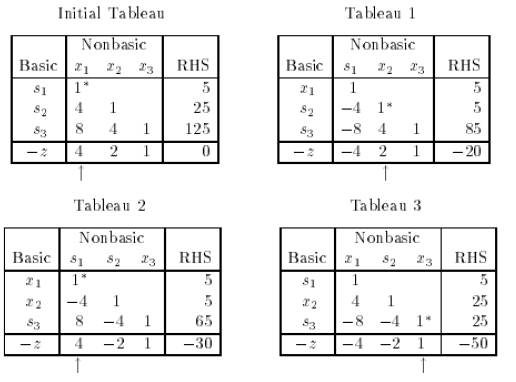
具体到Simplex算法的矩阵形式:
可以看出遍历了所有角, 因此, 我们说Simplex算法理论是最坏情况是指数形式的。
Simplex 近期突破
Simplex算法实际使用效果很好, 但是它的最坏情况很可能是指数时间(exponential time), 但是能够证明,平均情况下, Simplex算法是多项式时间的(polynomial time)。
南加州大学的腾尚华(Shang-Hua Teng)老师和他的合作者通过他们创建的平滑分析(Smooth analysis)解释了为什么Simplex算法会获得平均多项式时间的效果, 并且因此获得了2008年的Godel 计算理论大奖。有兴趣可以拜读他们的94页的论文“Smoothed Analysis of Algorithms: Why the Simplex Algorithm Usually Takes Polynomial Time”。
LP对偶
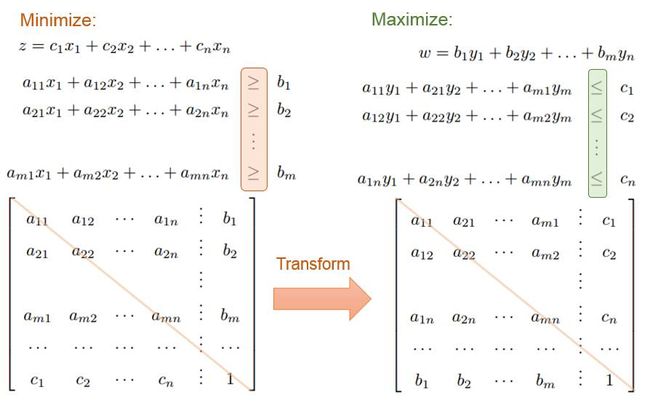
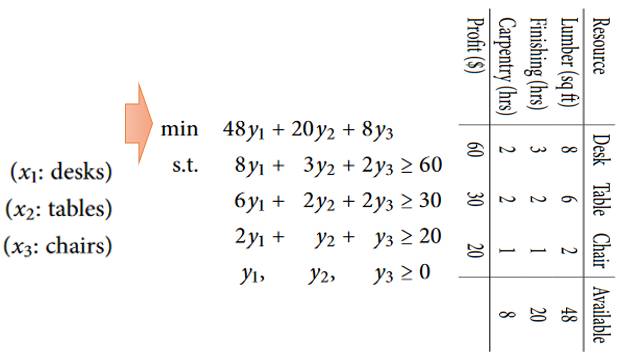
线性规划对偶(duality)问题的数学表述如下:
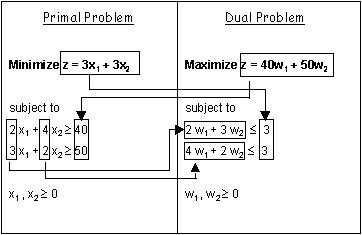
举个具体例子:
再举一个不是正方形矩阵的例子
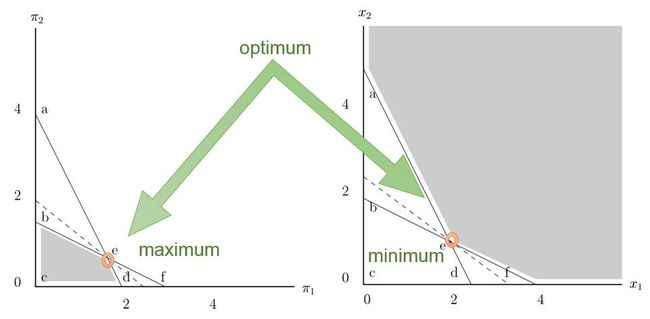
如果从图上直观来说, 最大和最小的最优值点在强凸情况下,是对应的。
如何来理解对偶呢?
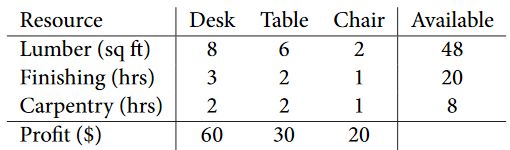
假设有个家具厂, 生产书桌, 餐桌和椅子。 但是生产这些东西, 需要资源: 木材, 时间, 和木工。 而这些资源都是有一定限额的。 同时我们知道每个产品对应的利润是多少。
那么很直观, 如何生产各个产品数量使得利润最高?
如果我们换个角度来看, 我们把y设定为单位资源的价格:
那么我们要购买全部资源的所需要的最小价格?
所以,我们购买全部资源的最小成本, 必须和产品的最大利润一致。
这样我们解释了一下, LP对偶问题的含义。 对于LP问题,Simplex算法也可以解决对偶问题的。
IPM 算法引述
IPM思想
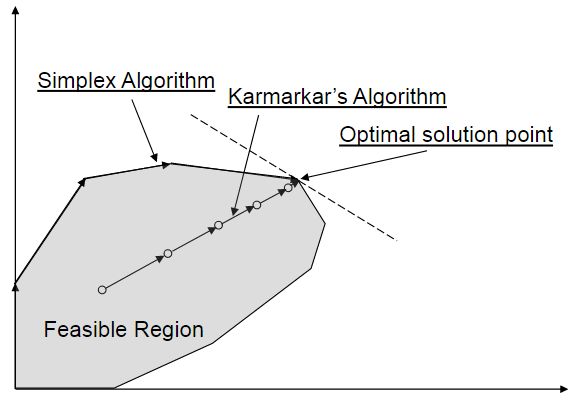
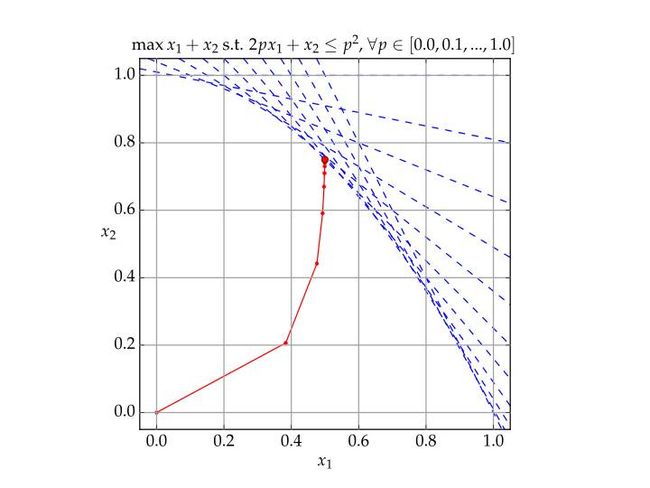
前面我们探讨了Simplex算法, 如果对比Karmarkar算法和Simplex最直观的比较, 如下, Simplex是沿着凸多面体(convex polyhedral)的边贪心走的。 而IPM是沿着内部(Interior)梯度点方向走的。
虽然,Karmarkar听上去很直观, 但是如何计算一个和梯度最接近的方向, 又如何选择点? 这些都是问题。
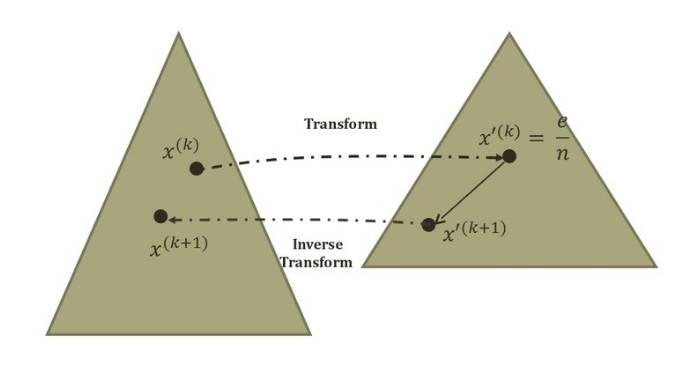
Karmarkar利用了反复投影的方式来达到最优点:
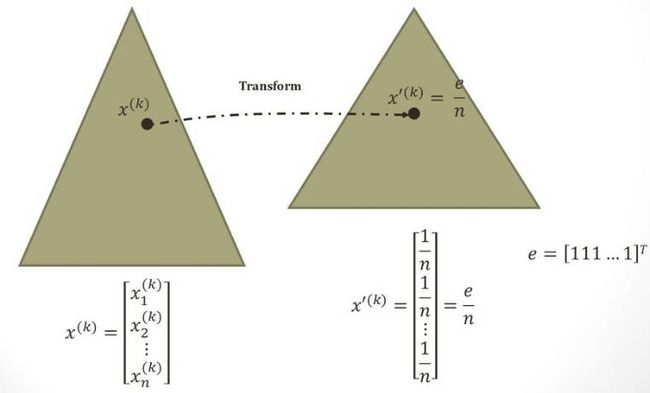
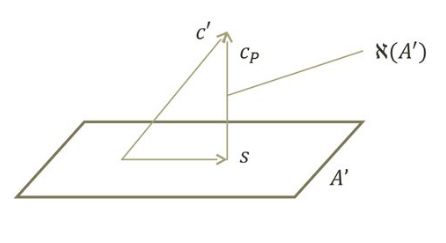
一个当前的点会transform到一个转换区域的中心点。 原来的多边形区域会变换到一个正多边形区域。 这样就存在一个仿射缩放(affine scaling)。
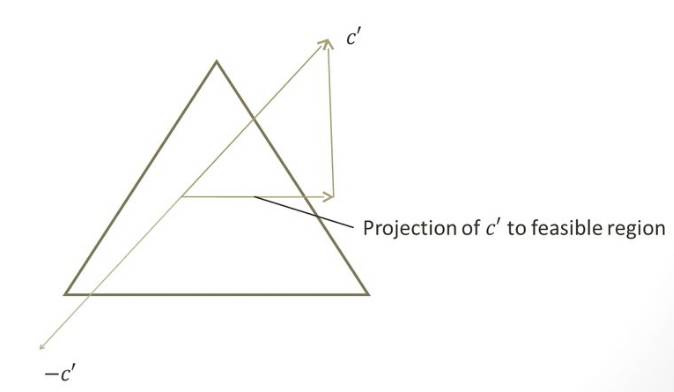
之后, 会在仿射区域进行投影(steepest-descent direction):
如果梯度方向不在区域内, 要进行矩阵的Col(A)空间。
在完成投影之后, 会在投影目标区域前进一步, 然后再反投影回原空间。
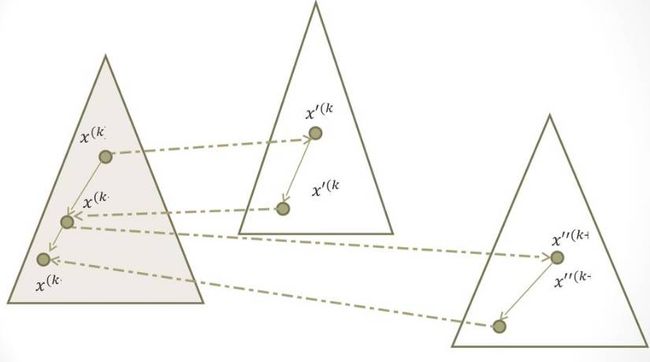
如果把整个过程再重复起来, 就能保证每次都往投影的梯度方向前进。
又由于每次都把当前点投影到中心, 然后前进。 所以算法会开始加速向梯度方向前进, 然后慢慢越来越准确的接近边缘区域。
对于Karmarkar算法发明后, 一下子轰动了整个世界, 居然有算法号称在处理大规模LP问题时候要比Simplex算法快10倍, 这下子像机场调度什么的就可以利用LP来解决了。 于是AT&T看到这个机会, 申请了专利。 又一下子引发了全世界对此的讨论, 因为到底这个基础性的算法,是要专利保护还是应该开放给全世界来提高效率。
于是有人开始争议说这个算法本身不算是创新,只是projected Newton barrier method 加上了 logarithmic barrier function在特殊参数的特解。 但是很多人并不认同这种说法。 可惜AT&T虽然申请了专利,并且还开发对应的软件, 但是获利不多了,软件只买了两套。 在2006年这个专利已经失效了。 但是这个专利有个明显的负作用了, 妨碍了Karmarkar本人与数学规划界进一步的合作探讨,发挥更大的影响力。 回头想想Google这样的公司开源一些基础性算法多么的明智。
对于Karmarkar算法本身的更多细节, 就在这里不展开细说了, 希望以后有机会再补充。
小结, 这里描述了LP规划的一般思路, 阐述了Simplex算法的思想, 尤其Pivot点是如此确定的。 对Karmarkar算法没有描述。 但是需要知道的是Karmarkar算法对应用LP到大规模线性规划里面, 例如机场调度中有着极大的影响。 尤其2008年腾尚华(Shang-Hua Teng)说明了Simplex为什么最坏不好, 但是通常很好,而获得Godel奖,他也是得过这个大奖的唯一华人。
参考:
http://www.mathsoc.spb.ru/pantheon/kantorov/
http://math.tutorvista.com/algebra/simplex-method.html
https://people.richland.edu/james/ictcm/2006/3dsimplex.html
https://inst.eecs.berkeley.edu/~ee127a/book/login/l_intro_some_pbs.html
http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Dantzig_George.html
http://mathoverflow.net/questions/127423/how-many-vertices-can-a-convex-polytope-have
http://math.uww.edu/~mcfarlat/s-prob.htm
http://doc.mbalib.com/view/9cf748a18c322f527d989e746e55dcd0.html
https://www.utdallas.edu/~scniu/OPRE-6201/documents/LP10-Special-Situations.pdf
http://dictionnaire.sensagent.leparisien.fr/Karmarkar's%20algorithm/en-en/