赫夫曼树与赫夫曼编码
一、赫夫曼树
在数据膨胀、信息爆炸的今天,数据压缩的意义不言而喻。谈到数据压缩,就不能不提赫夫曼(Huffman)编码,赫夫曼编码是首个实用的压缩编码方案,即使在今天的许多知名压缩算法里,依然可以见到赫夫曼编码的影子。
另外,在数据通信中,用二进制给每个字符进行编码时不得不面对的一个问题是如何使电文总长最短且不产生二义性。根据字符出现频率,利用赫夫曼编码可以构造出一种不等长的二进制,使编码后的电文长度最短,且保证不产生二义性。
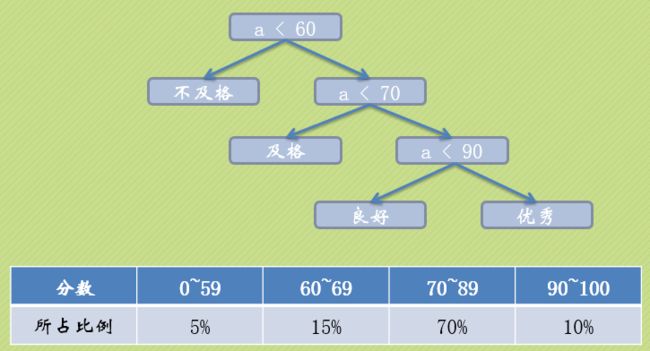
以下程序在效率上有什么问题呢?
if( a < 60 )
printf(“不及格”);
else if( a < 70 )
printf(“及格”);
else if( a < 90 )
printf(“良好”);
else
printf(“优秀”);
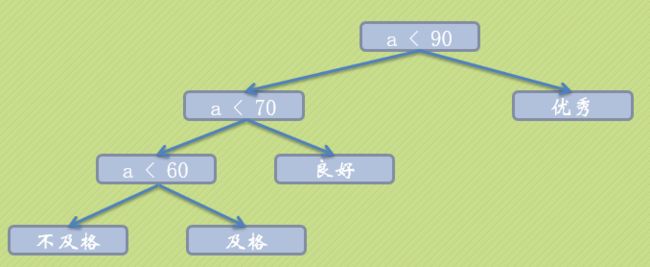
如果我们把判断流程改为以下,效果可能有明显的改善:对于判断良好效率更高了。
赫夫曼树定义与原理
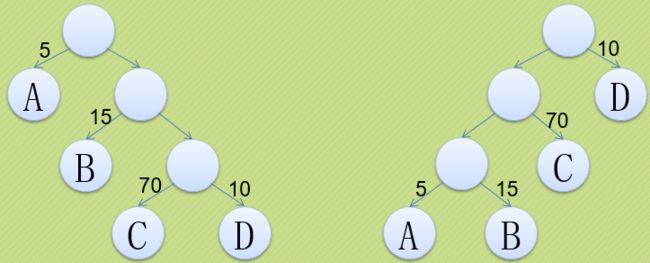
把这两棵二叉树简化成叶子结点带权的二叉树
(注:树结点间的连线相关的数叫做权,Weight)。
如图:A表示不及格,B表示及格,C表示良好,D表示优秀
5%同学不及格,15%同学及格,70%同学良好,10%同学优秀
- 结点的路径长度:从根结点到该结点的路径上的连接数。
- 树的路径长度:树中每个叶子结点的路径长度之和。
- 结点带权路径长度:结点的路径长度与结点权值的乘积。
- 树的带权路径长度:WPL(Weighted Path Length)是树中所有叶子结点的带权路径长度之和。
WPL的值越小,说明构造出来的二叉树性能越优。
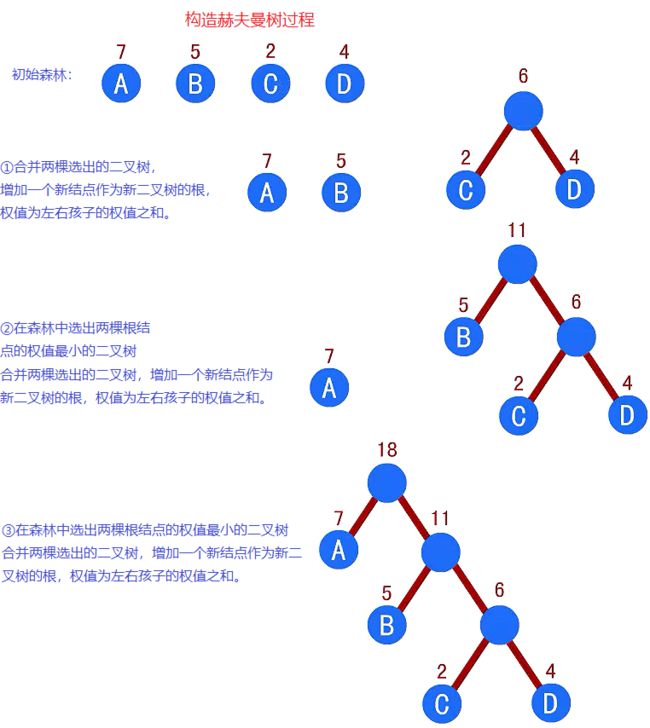
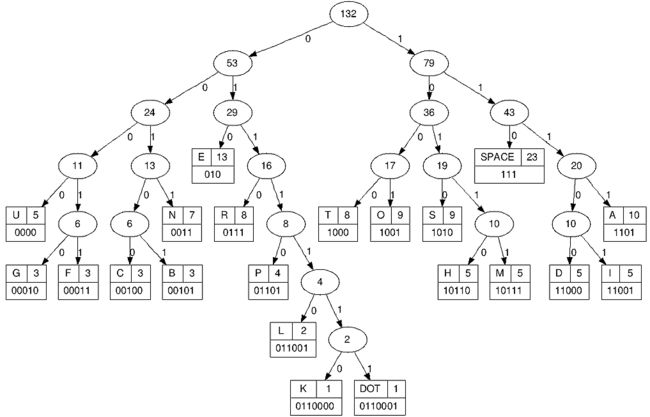
构造出最优的赫夫曼树,如图:
二、赫夫曼编码
当年赫夫曼的草图:
赫夫曼编码可以很有效地压缩数据(通常可以节省20%~90%的空间,具体压缩率依赖于数据的特性)。
名词解释:定长编码,变长编码,前缀码
- 定长编码:像ASCII编码
- 变长编码:单个编码的长度不一致,可以根据整体出现频率来调节
- 前缀码:所谓的前缀码,就是没有任何码字是其他码字的前缀
步骤:
- build a priority queue
- build a huffmanTree
- build a huffmanTable
- encode
- decode
代码实现:
main.cpp:
#include
#include
#include "huffman.h"
int main(void)
{
//We build the tree depending on the string
htTree *codeTree = buildTree("beep boop beer!");
//We build the table depending on the Huffman tree
hlTable *codeTable = buildTable(codeTree);
//We encode using the Huffman table
encode(codeTable,"beep boop beer!");
//We decode using the Huffman tree
//We can decode string that only use symbols from the initial string
decode(codeTree,"0011111000111");
//Output : 0011 1110 1011 0001 0010 1010 1100 1111 1000 1001
return 0;
}
huffman.h:
#pragma once
#ifndef _HUFFMAN_H
#define _HUFFMAN_H
//The Huffman tree node definition
typedef struct _htNode {
char symbol;
struct _htNode *left, *right;
}htNode;
/*
We "encapsulate" the entire tree in a structure
because in the future we might add fields like "size"
if we need to. This way we don't have to modify the entire
source code.
*/
typedef struct _htTree {
htNode *root;
}htTree;
//The Huffman table nodes (linked list implementation)
typedef struct _hlNode {
char symbol;
char *code;
struct _hlNode *next;
}hlNode;
//Incapsularea listei
typedef struct _hlTable {
hlNode *first;
hlNode *last;
}hlTable;
htTree * buildTree(char *inputString);
hlTable * buildTable(htTree *huffmanTree);
void encode(hlTable *table, char *stringToEncode);
void decode(htTree *tree, char *stringToDecode);
#endif
huffman.cpp:
#include
#include
#include
#include "huffman.h"
#include "pQueue.h"
void traverseTree(htNode *treeNode, hlTable **table, int k, char code[256])
{
//If we reach the end we introduce the code in the table
if(treeNode->left == NULL && treeNode->right == NULL)
{
code[k] = '\0';
hlNode *aux = (hlNode *)malloc(sizeof(hlNode));
aux->code = (char *)malloc(sizeof(char)*(strlen(code)+1));
strcpy(aux->code,code);
aux->symbol = treeNode->symbol;
aux->next = NULL;
if((*table)->first == NULL)
{
(*table)->first = aux;
(*table)->last = aux;
}
else
{
(*table)->last->next = aux;
(*table)->last = aux;
}
}
//We concatenate a 0 for each step to the left
if(treeNode->left!=NULL)
{
code[k]='0';
traverseTree(treeNode->left,table,k+1,code);
}
//We concatenate a 1 for each step to the right
if(treeNode->right!=NULL)
{
code[k]='1';
traverseTree(treeNode->right,table,k+1,code);
}
}
hlTable * buildTable(htTree * huffmanTree)
{
//We initialize the table
hlTable *table = (hlTable *)malloc(sizeof(hlTable));
table->first = NULL;
table->last = NULL;
//Auxiliary variables
char code[256];
//k will memories the level on which the traversal is
int k=0;
//We traverse the tree and calculate the codes
traverseTree(huffmanTree->root,&table,k,code);
return table;
}
htTree * buildTree(char *inputString)
{
//The array in which we calculate the frequency of the symbols
//Knowing that there are only 256 posibilities of combining 8 bits
//(256 ASCII characters)
int * probability = (int *)malloc(sizeof(int)*256);
//We initialize the array
for(int i=0; i<256; i++)
probability[i]=0;
//We consider the symbol as an array index and we calculate how many times each symbol appears
for(int i=0; inputString[i]!='\0'; i++)
probability[(unsigned char) inputString[i]]++;
//The queue which will hold the tree nodes
pQueue * huffmanQueue;
initPQueue(&huffmanQueue);
//We create nodes for each symbol in the string
for(int i=0; i<256; i++)
if(probability[i]!=0)
{
htNode *aux = (htNode *)malloc(sizeof(htNode));
aux->left = NULL;
aux->right = NULL;
aux->symbol = (char) i;
addPQueue(&huffmanQueue,aux,probability[i]);
}
//We free the array because we don't need it anymore
free(probability);
//We apply the steps described in the article to build the tree
while(huffmanQueue->size!=1)
{
int priority = huffmanQueue->first->priority;
priority+=huffmanQueue->first->next->priority;
htNode *left = getPQueue(&huffmanQueue);
htNode *right = getPQueue(&huffmanQueue);
htNode *newNode = (htNode *)malloc(sizeof(htNode));
newNode->left = left;
newNode->right = right;
addPQueue(&huffmanQueue,newNode,priority);
}
//We create the tree
htTree *tree = (htTree *) malloc(sizeof(htTree));
tree->root = getPQueue(&huffmanQueue);
return tree;
}
void encode(hlTable *table, char *stringToEncode)
{
hlNode *traversal;
printf("\nEncoding\nInput string : %s\nEncoded string : \n",stringToEncode);
//For each element of the string traverse the table
//and once we find the symbol we output the code for it
for(int i=0; stringToEncode[i]!='\0'; i++)
{
traversal = table->first;
while(traversal->symbol != stringToEncode[i])
traversal = traversal->next;
printf("%s",traversal->code);
}
printf("\n");
}
void decode(htTree *tree, char *stringToDecode)
{
htNode *traversal = tree->root;
printf("\nDecoding\nInput string : %s\nDecoded string : \n",stringToDecode);
//For each "bit" of the string to decode
//we take a step to the left for 0
//or ont to the right for 1
for(int i=0; stringToDecode[i]!='\0'; i++)
{
if(traversal->left == NULL && traversal->right == NULL)
{
printf("%c",traversal->symbol);
traversal = tree->root;
}
if(stringToDecode[i] == '0')
traversal = traversal->left;
if(stringToDecode[i] == '1')
traversal = traversal->right;
if(stringToDecode[i]!='0'&&stringToDecode[i]!='1')
{
printf("The input string is not coded correctly!\n");
return;
}
}
if(traversal->left == NULL && traversal->right == NULL)
{
printf("%c",traversal->symbol);
traversal = tree->root;
}
printf("\n");
}
pQueue.h:
#pragma once
#ifndef _PQUEUE_H
#define _PQUEUE_H
#include "huffman.h"
//We modify the data type to hold pointers to Huffman tree nodes
#define TYPE htNode *
#define MAX_SZ 256
typedef struct _pQueueNode {
TYPE val;
unsigned int priority;
struct _pQueueNode *next;
}pQueueNode;
typedef struct _pQueue {
unsigned int size;
pQueueNode *first;
}pQueue;
void initPQueue(pQueue **queue);
void addPQueue(pQueue **queue, TYPE val, unsigned int priority);
TYPE getPQueue(pQueue **queue);
#endif
pQueue.cpp:
#include "pQueue.h"
#include
#include
void initPQueue(pQueue **queue)
{
//We allocate memory for the priority queue type
//and we initialize the values of the fields
(*queue) = (pQueue *) malloc(sizeof(pQueue));
(*queue)->first = NULL;
(*queue)->size = 0;
return;
}
void addPQueue(pQueue **queue, TYPE val, unsigned int priority)
{
//If the queue is full we don't have to add the specified value.
//We output an error message to the console and return.
if((*queue)->size == MAX_SZ)
{
printf("\nQueue is full.\n");
return;
}
pQueueNode *aux = (pQueueNode *)malloc(sizeof(pQueueNode));
aux->priority = priority;
aux->val = val;
//If the queue is empty we add the first value.
//We validate twice in case the structure was modified abnormally at runtime (rarely happens).
if((*queue)->size == 0 || (*queue)->first == NULL)
{
aux->next = NULL;
(*queue)->first = aux;
(*queue)->size = 1;
return;
}
else
{
//If there are already elements in the queue and the priority of the element
//that we want to add is greater than the priority of the first element,
//we'll add it in front of the first element.
//Be careful, here we need the priorities to be in descending order
if(priority<=(*queue)->first->priority)
{
aux->next = (*queue)->first;
(*queue)->first = aux;
(*queue)->size++;
return;
}
else
{
//We're looking for a place to fit the element depending on it's priority
pQueueNode * iterator = (*queue)->first;
while(iterator->next!=NULL)
{
//Same as before, descending, we place the element at the begining of the
//sequence with the same priority for efficiency even if
//it defeats the idea of a queue.
if(priority<=iterator->next->priority)
{
aux->next = iterator->next;
iterator->next = aux;
(*queue)->size++;
return;
}
iterator = iterator->next;
}
//If we reached the end and we haven't added the element,
//we'll add it at the end of the queue.
if(iterator->next == NULL)
{
aux->next = NULL;
iterator->next = aux;
(*queue)->size++;
return;
}
}
}
}
TYPE getPQueue(pQueue **queue)
{
TYPE returnValue;
//We get elements from the queue as long as it isn't empty
if((*queue)->size>0)
{
returnValue = (*queue)->first->val;
(*queue)->first = (*queue)->first->next;
(*queue)->size--;
}
else
{
//If the queue is empty we show an error message.
//The function will return whatever is in the memory at that time as returnValue.
//Or you can define an error value depeding on what you choose to store in the queue.
printf("\nQueue is empty.\n");
}
return returnValue;
}