最近这破事贼多,都没有什么时间写写博客,都好久都没有更新博客了!不过平常看jdk源码的时候有很大的感触,就是基础真的很重要,那什么是基础呢?除了java的基本语法之外,最基础的莫过于原码,反码和补码了以及基本的运算了!
由于我是编程半路出家,最开始的时候学过一点这些东西,当时只是感觉,擦!我是写代码的,这些原码什么的有个鸡儿用,有时间看这个还不如多写点代码!但是现在,看了不少源码,回头一看却突然发现自己基础太薄弱了,赶紧补一下基础,装作基础很扎实的样子@_@
1.原码、反码和补码
大家应该都知道,数据在计算机中是以二进制的形式存在的,比如 byte a = 6; byte b = -6
分为两种情况来说,一种是正数,一种是负数;对于正数6来说,原码就是0000 0110,反码和补码也是这个;而对于-6来说,原码就是1000 0110,这是为什么呢?因为最高位(最左边的)是表示符号,0表示正数,1表示负数;
不管是byte,short,int还是其他的数字,最高位都是用来表示符号的,所以-6的原码就是1000 0110,负数的反码就是符号不变,其他的取反,就是1111 1001;负数的补码就是在反码的基础上加1就行了,由于是二进制的,是逢2进1,所以补码就是:1111 1010,;
注意:计算机中的加减运算(计算机中只有加法,可以通过加法表示减法,就是用过补码的形式,看下面栗子)指的是补码之间的运算!而且负数在计算机中是以补码的形式存在并参与运算的,如果要变为十进制,就首先需要变为原码然后才能变为十进制或其他进制的数;
那么0怎么表示呢?我们可以简单看看:0 = 6-6 = 6+(-6)= [0000 0110]补+[1111 1010]补=[0000 0000]补=[0000 0000]原,那么有人要问了,补码1000 0000那又表示多少呢?再看一个简单的-1-127=(-1)
+(-127)= [1000 0001]原+[1111 1111]原 = [1111 1111]补+[1000 0001]补 = [1000 0000]补=[0000 0000]原,两个对比一下,如果都使用原码的话同一个原码[0000 0000]原可以表示两个数0和-128,而用补码的话却可以一个补码对应单独的一个数,很明显,一个补码对应一个数更符合我们的需求!!!
补充一下,对于负数来说,原码和反码之间相互转化,试着理解着记忆:
原码------>反码:符号位不变,其他位取反 ;比如 [1000 0001]原 = [1111 1110]反
原码------>补码:符号位不变,其他位取反,然后+1;比如 [1000 0001]原 = [1111 1111]补
反码------->原码:符号位不变,其他位取反;比如 [1111 1110]反 = [1000 0001]原
反码------->补码:+1 ;比如 [1111 1110]反 = [1111 1111]补
补码------->原码:符号位不变,其他位取反,然后+1;比如 [1111 1111]补 = [1000 0001]原
补码--------->反码:先变为原码,然后变反码;比如 [1111 1111]补 =[1111 1110]反
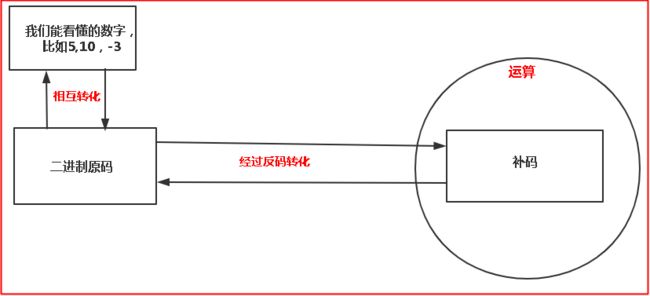
这些都是基本的东西,只要记住在计算机中运算的话,都是以补码的形式,而且这里就会涉及到一个过程,画一个简单的图,计算机中运算都是用补码来进行的;而中间的转化过程计算机可以十分迅速的转化,这个就不用我们操心;下面我们就看看那个运算到底包括哪些运算。。。
2.基本的运算
说起现实中的运算,无非就是四则运算,加减乘除,而对应于计算机中也有加减乘除,加减已经在上面说了,可以用补码的加法来实现加减,但是乘除呢?在这里我们就说说最简单的乘除法啊,乘以2和除以2这种,如果是乘除其他数还是比较复杂的,暂时我也没有什么兴趣研究,有兴趣的小伙伴可以查查计算机中乘除法的实现,你会沉迷其中不可自拔!
以byte类型来举例,byte类型最高位是符号位,所以范围是在1111 1111到01111 1111之间,变成十进制也就是-127到127,加上0000 0000这个原码对应两个数0和-128,所以整个的范围就是-128到127;
乘除也是分为两大块,正数和负数;
2.1 正数乘2运算(左移用<<表示)
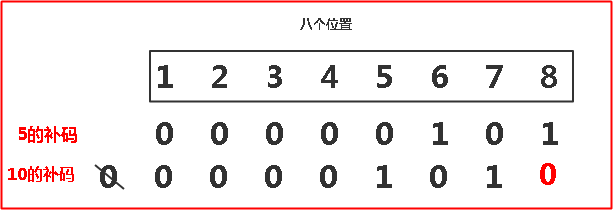
我们看看一个简单的数(这里我正数也写一下补码):byte a = 5; 5的原码为:[0000 0101]原=[0000 0101]补 ;乘以2就等于10,原码为[0000 1010]原=[0000 1010]补
看看这两个补码有什么关系?就是将5的补码最右边添加一个0,最左边去掉一个0!最好是将5的补码看作一个整体,这个整体向左移动一位,左边超过的位数直接去掉,右边空的位置添0
这个时候会有一个问题,假如二进制补码是0100 0000,也就是64,向左移动一位,你觉得是多少?答案是-128,按理来说应该是正数的128啊,为什么是负的呢?记住,这个移位操作是会覆盖符号位的,往左移动一位的补码是1000 0000,注意,这里千万不要变成原码,在第一节中说过了补码为1000 0000的就是-128(这两个补码一定要注意点,很特殊,0000 0000代表十进制的0,1000 0000代表十进制的-128!千万不要变成原码比较,因为他们的原码都是0000 0000无法区分)
public void num() { byte a = 64; byte b = (byte) (a<<1); System.out.println(b);//-128 }
2.2 正数除2运算(右移用>>表示)
既然往左移动一位是乘以2,那么往右移动一位肯定是除以2了!但是记住一个规律,往右移动的话,右边超出来的部分去掉,左边空出来的位置添加和符号位相同的数!(记住了规律这个负数的右移一样的)
举个例子,65的补码0100 0001,向右移动一位,补码应该是0010 0000,记住,此时最左边的0是根据符号位是0才添加的0,是正数,右移后的原码和补码一样,那么变成十进制应该是32,这里可以看出一个大于0的奇数右移一位的结果就是除以2然后向下取整,偶数的话直接就是除以2了
public void num() { byte a = 65; byte b = (byte) (a>>1); System.out.println(b);//32 }
2.3 负数乘2运算(<<)
正数其实比较容易,但是负数的话就稍微麻烦一点!例如-127的补码是1000 0001,左移一位的补码0000 0010,由于这个补码是正的,所以原码也是这个,变成十进制就是2,有没有觉得特别有意思,哈哈哈!知道为什么吗?因为byte的范围是-128到127啊,只要是超过了这个范围的就会变成你想不到的数!
再举个没有超过范围的例子,-6的补码是1111 1010,左移一位的补码就是1111 0100,由于是负的,变成原码为1000 1100,也就是对应十进制的-12,这个结果和想象的一样!
2.4 负数除2运算(>>)
记住在2.2中说的一句话,向右移动的话,最右边超过的部分直接去掉,左边空出来的位置填上和符号位相同的数!说起来很抽象,举个栗子:-6的补码是1111 1010,往右移动一个位置的补码就是1111 1101,是负的,变成原码就知道对应的十进制是多少了。。。。
2.5.无符号右移(>>>)
本来都说了正负数的左移和右移应该就说完了,但是呢,还有一个比较特殊的运算方式,就是无符号右移(注意只有无符号右移,没有无符号左移啊!),简单的来说就是不管正数负数,只要是右移的话,最右边超过的部分直接丢掉,左边空出来的位置都添0就ok了!
好像也没什么可说的,简单举个栗子吧!-6的补码是1111 1010,无符号右移一位的补码就是0111 1101,正的,原码和补码一样,所以对应的十进制是应该是125,然而实际情况有点问题,代码如下:
@org.junit.Test public void num() { byte a = -6; byte b = (byte) (a>>>1); System.out.println(b);//-3 }
打印的结果为什么是-3呢?,这里就有一个小小的细节操作,在进行右移操作的时候,首先会将该byte类型的数变成int类型的,对int类型的变原码,然后变补码,移位操作之后,取后8位变为byte类型,然后变原码,最后转十进制。。。。是不是贼麻烦!还是以上面的-6为栗子,-6要进行无符号右移,所以-6的原码应该是32位的
10000000 00000000 00000000 00000110 //原码 11111111 11111111 11111111 11111010//补码 011111111 11111111 11111111 1111101//无符号右移一位 11111101//取后八位,就是byte类型的补码 10000011//byte类型原码,对应十进制是-3
3.简单总结一下
由于我们是用一个byte类型的为例,这也是为了方便举例子,不然用个int类型的,随便一个数写出原码都是一大串,看着都眼花。。。其实byte类型的移位运算弄清楚了,其他的类型一样的,看了这么多,不知道大家有没有总结出来一点规律,我就说说我的理解吧!
首先,我们要明确当前的数是一个什么类型,进行移位操作之后会不会超出这个类型的范围,如果超出了,我们是不能直接得出乘以2或者除以2这种简单的结论的,会得出一个意想不到的数字;
然后,如果移位操作之后没有超过当前类型的范围,那么就大胆的说左移一位是乘以2,右移一位是除以2向下取整吧!!!
再然后,对于一个正数,左移一位就是最高位去掉,最低位添0;右移一位最高位添加和符号位一样的数,最低位去掉;对于负数而言,也是一样的,就不多说了
最后,就是无符号右移,这里要注意先要变成int类型的二进制原码,变补码,然后进行移位操作,截取后8位为我们需要的byte类型的补码,再变原码,最后就是变成十进制的了。。。
4."或"、"与"、"非"、"异或"
请注意“或”、“与”、“非”和java中的||、&&、!别弄混淆了,java中的这几个是用来进行逻辑判断的,而我们这里的“或”“与”“异或”这几个是用来计算二进制的,完全没有什么相关,虽然写法有点类似,“或”用一根竖线表示|,与用一个&表示,非用~表示,"异或"用^表示,下面就简单说说他们的作用:
或:在二进制中,两个操作数进行或操作,只要有一个为1,结果就为1,否则就为0;举个例子,-6|3,首先将各自都变为补码,也就是变为(1111 1011)|(0000 0011),根据下图,最后计算的补码为1111 1011,变为原码为1000 0101,对应十进制的-5,所以-6|3的结果就是-5!很简单吧,现在应该知道操作数是什么了吧!
public void num() { byte a = -6|3; System.out.println(a);//-5 }
与:两个操作数同时为1,结果才是1,否则为0;
异或:看这个名字就知道了,两个操作数不同结果就是1,否则为0;
非:就是对自己取反(符号位也要取反),用法如下,因为-6的补码是1111 1010,取反之后的补码0000 0101,对应十进制的5
public void num() { byte a = -6; System.out.println(~a);//5 }
5.简单练习
如果把上面的都看懂了,理解了那么下面这个就很容易了;
直接说一下这个方法的用处,就是你随便输入一个int类型的数,它都会给你返回一个2的次幂数,比如1,2,4,8,16.32.64等这种数(1等于2的零次幂,也是2的次幂数)
static final int tableSizeFor(int cap) { int n = cap - 1; n |= n >>> 1; n |= n >>> 2; n |= n >>> 4; n |= n >>> 8; n |= n >>> 16; return (n < 0) ? 1 :n + 1; }
这个方法其实很容易,就是将传进去的int类型的cap首先减一,赋值给n,然后n进行5次无符号右移操作,每次右移之后都和n进行"或"操作,最后判断n如果小于零,就返回1,否则就返回n+1
我们就比如传入5,那么n等于4,无符号右移一位然后与n进行“或”操作,由于位数太多,我就直接写结果了:
00000000 00000000 00000000 00000100//n的二进制补码 00000000 00000000 00000000 00000110//无符号右移一位然后和n进行“或”操作 00000000 00000000 00000000 00000111//无符号右移两位然后和n进行“或”操作 00000000 00000000 00000000 00000111//无符号右移四位然后和n进行“或”操作 00000000 00000000 00000000 00000111//无符号右移八位然后和n进行“或”操作 00000000 00000000 00000000 00000111//无符号右移十六位然后和n进行“或”操作
最后右移16位的n结果应该是7,再到return语句,返回的是n+1,也就是返回8,而8就是2^3,满足前面说的返回一个2的次幂数;有兴趣的可以试试其他的数,返回的结果肯定是2的次幂数,有没有觉得这个算法特别牛逼!简直无敌呀!
如果你看懂了这个方法的话,你可以打开你的Eclipse或者IDEA,用jdk1.8找到一个叫做HashMap的类,你就可以看到这个方法(当然我把最后的return语句稍微变了一点),这个就是HashMap进行扩容的一个方法,所以我们可以知道HashMap初始化以及扩容之后的容量,总是2的幂级数,是不是很容易啊!
当然有的时候面试,面试官会问你为什么HashMap的容量要设置为2的幂级数啊?这个问题就有点东西了,首先你可以把这部分算法给他说一下,玛德!源码就是这样写的啊!你还问我为什么?然后还要说的话,其实也很容易,还涉及到了一个“与”操作,看看这个(n - 1) & hash,hash就是将一个键值对的key通过hash算法得到的一个很大的数,而n就是hashmap长度,也就是2的次幂数,那么(n - 1) & hash代表什么呢?
有兴趣的可以玩一下,其实就是相当于hash%n,就是相当于对n取余,这个余数肯定是小于n,这样首先可以保证得到的数组中的索引不会超过数组,而且用这种方式可以保证数据是均匀的分布在hashmap中的那个数组中,我这里也就是简单提了一下,很容易的!
有兴趣的可以看看这个老哥的一篇博客https://www.iteye.com/topic/539465,这篇博客是说的比较清楚的了!最好看之前先把jdk8的HashMap源码看一遍,哈哈