堆
堆也被称为优先队列,队列是先进先出,队尾插入,队头删除,而堆也是堆底插入,堆顶删除。
栈
栈先进后出,栈顶插入和删除。它是一种运算受限的线性表。
队列
队列是先进先出,队尾插入,队头删除。动态的创建,动态是否,因而不存在溢出问题。
散列表
又称哈希表,是把关键码根据映射函数映射到表中一个地址中,以加快查找速度。
散列地址冲突
是因为多个关键码的映射地址相同。
解决方法
开放地址法:出现冲突,顺序的寻找写一个地址是否冲突,不冲突则放入,否则,继续向下寻找。
链地址法:每个哈希地址单元为一个同义链表,来维护相同地址的关键码。
二叉树
第i层最大为2^(i-1),深度为k的二叉树最多有2^k-1 个结点,n个结点高度至少log2(n+1)。任一棵二叉树,n0=n2+1。
前序遍历:
//二叉树前序遍历递归
void PreOrder(TreeNode* root)
{
if(root)
{
cout << root->val << endl;
PreOrder(root->left);
PreOrder(root->right);
}
}
//二叉树前序遍历非递归
void PreOrder(TreeNode* root)
{
stack
while(root != nullptr || !s.emtpy())
{
if(root)
{
s.push(root);
cout << root->val << endl;
root = root->left;
}
else
{
root = s.top();
s.pop();
if(root)
{
root = root->right;
}
}
}
}
中序遍历:
//二叉树中序遍历递归
void InOrder(TreeNode* root)
{
if(root)
{
InOrder(root->left);
cout << root->val << endl;
InOrder(root->right);
}
}
//二叉树中序遍历非递归
void InOrder(TreeNode* root)
{
stack
while(root)
{
s.push(root);
root = root->left;
}
if(!s.empty())
{
root = s.top();
cout << root->val << endl;
s.pop();
if(root)
{
root = root->right;
}
}
}
后序遍历:
//二叉树后序遍历递归
void PostOrder(TreeNode* root)
{
if(root)
{
PostOrder(root->left);
PostOrder(root->right);
cout << root->val << endl;
}
}
//二叉树后序遍历非递归
void PostOrder(TreeNode* root)
{
TreeNode* cur;
TreeNode* pre = nullptr;
stack
if(root)
{
s.push(root);
}
while(!s.empty())
{
cur = s.top();
if(cur->left == nullptr && cur->right == nullptr || pre && (cur->left == pre || cur->right == pre))
{
cout << cur->val << endl;
pre = cur;
s.pop();
}
else
{
if(cur->right)
{
s.push(cur->right);
}
if(cut->left)
s.push(cur->left);
}
}
}
层次遍历:
//层次遍历
void LevelOrder(TreeNode* root)
{
if(root == nullptr)
return;
queue
if(root)
q.push(root);
while(!q.empty())
{
TreeNode* tmp = q->front();
cout << tmp->val << endl;
q.pop();
if(tmp->left)
{
q.push(tmp->left);
}
if(tmp->right)
{
q.push(tmp->right);
}
}
}
二叉查找树:
又称二叉搜索树,二叉排序树。即中序遍历有序,若左子树不空,则左子树的值都小于根结点的值,若右子树不空,右子树的值都大于根结点,不存在值相同的结点。
完全二叉树:
只有最小两层的结点度小于2,且全都左连续。
平衡二叉树:
每个结点的左子树和右子树高度差不超过1。
b 树、b+ 树
首先 b 树属于多叉树又名平衡多路查找树
其规则是
所有节点关键字是按递增顺序排列,并遵循左小右大规则
子节点数,非叶子节点的子节点数大于 1 且小于 M,且 M > 2,空树除外
关键字数,枝接点的关键字数量大于等于 ceil(m/2)-1 个且小于等于 M-1 个(注:ceil() 是个朝正无穷方向取整的函数,比如 ceil(1,1) = 2)
叶节点的指针为空且叶节点具有相同的深度
而对于 b+ 树,是 b 树的一个升级版,相对于 b 树而言 b+ 树更充分利用了节点的空间,让查询速度更加稳定,其速度完全接近二分查找。
红黑树:
一种特殊的二叉查找树。
特性:
1、每个结点非红即黑。
2、根结点黑色。
3、每个叶子结点黑色。
4、若结点为红色,其子节点为黑色。
5、从一个结点到该子孙结点的所有路径上包含相同数目的黑结点。
红黑树的基本操作
红黑树的基本操作是添加、删除,在对红黑树进行添加删除之后,都会用到旋转方法(之所以要进行旋转,是因为要在插入删除后还必须满足红黑树的性质)
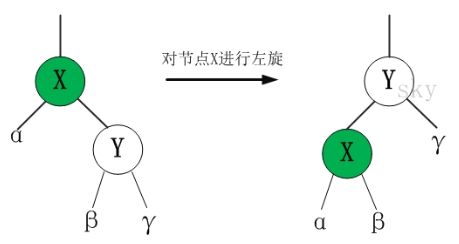
左旋
右旋
红黑树如何进行插入删除?
插入
如果父节点为黑色,直接插入不处理
如果父节点为红色,叔叔节点为红色,则父节点和叔叔节点变为黑色,祖先节点变为红色,将节点操作转换为祖先节点
如果当前节点为父亲节点的右节点,则以父亲结点为中心左旋操作
如果当前节点为父亲节点的左节点,则父亲节点变为黑色,祖先节点变为红色,以祖先节点为中心右旋操作
删除
先按照排序二叉树的方法,删除当前节点,如果需要转移即转移到下一个节点
当前节点,必定为这样的情况:没有左子树。
删除为红色节点,不需要处理,直接按照删除二叉树节点一样
如果兄弟节点为黑色,兄弟节点的两个子节点为黑色,则将兄弟节点变为红色,将着色转移到父亲节点
如果兄弟节点为红色,将兄弟节点设为黑色,父亲结点设为红色节点,对父亲结点进行左旋操作
如果兄弟节点为黑色,左孩子为红色,右孩子为黑色,对兄弟节点进行右旋操作
如果兄弟节点为黑色,右孩子为红色,则将父亲节点的颜色赋值给兄弟节点,将父亲节点设置为黑色,将兄弟节点的右孩子设为黑色,对父亲节点进行左旋
红黑树、b 树、b+ 树区别
红黑树的深度比较大,而B+和B-的深度则相对要小一些,而B+较B-则将数据都保存在叶子节点,同时通过链表的形式将他们连接在一起。