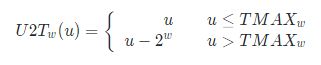整数的表示与编码

补一下CSAPP的笔记

计算机中整数的表示与编码

计算机中的整数主要包括两种：有符号数与无符号数。

无符号数的编码

其中有符号数的表示方法与传统二进制一致。
假设有一个整数数据类型有w位。我们可以将位向量写成

在这个编码中，每个x_i都取值为0或1。我们用一个函数来表示B2U_w来表示：

无符号数的编码方式实际上与我们所知道的二进制编码方式是一致的。唯一要注意的是无符号数的编码具有唯一性，也就是说一个数字只能有一个无符号数编码。这是因为B2U_w是一个双射。

有符号数的编码

有符号数的编码主要有三种方式：原码、补码与反码。我曾经写过一篇博客来进行探究，这里不赘述。
关于补码的由来和作用
需要说明的是：补码也具有唯一性，原码与反码不具备这种性质，因为0在原码与反码中有两种解释。

有符号数与无符号数之间的转换

有符号数转无符号数

C语言中提供了在不同数据类型中做强制类型转换的方法，对于无符号整数与有符号整数之间的转换方式，大多数系统上默认的是底层的位不变，由此我们能推出有符号数与无符号数之间的转换。
关于这些的转换的的过程和原理，在此不赘述。这里直接给出公式：
一个数的编码方式从无符号编码(补码)转换为有符号编码后的数值公式为:

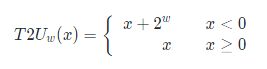
如果有符号数的真值小于0那么，把真值加上2^w即为其无符号真值，如果真值大于0，那么不变。
我们用一段C语言代码举例：

#include
#include
#include
int main(void)
{
    int i = -1;
    unsigned int j = (unsigned int)i;
    printf("%u\n", j);
    printf("%u\n", UINT_MAX);
    system("pause");
}

VS2017下的运行结果：

数据类型int的大小为8字节，32位，把-1转换成无符号数需要加上2₃₂，结果为2₃₂-1，正好为无符号数编码的最大值，所以与UINT_MAX的值一致。

无符号数转有符号数

直接给出公式：

C语言代码测试实例：

#include
#include
#include
int main(void)
{
    unsigned int i = UINT_MAX;
    int j=(int)i;
    printf("%d", j);
    system("pause");
}

VS2017下的运行结果：

需要说明的是，在VS2017的环境下，上面两个程序经过测试即使不使用强制类型转换也可以得到正确的结果，其一是C语言中如果发现左右两边数据类型不一致会自动把数据往左边的类型转换，其二是，printf中的格式说明符也会自动执行类型转换，这里使用强制类型转换只是为了让转换看起来更加清晰。

无符号整数与有符号整数互相转换可能遇到的问题

由于C语言对同时包含有符号和无符号数表达式的这种处理方式，出现了一些奇特的行为。当执行一个运算时如果它的一个运算数是有符号的而另一个是无符号的，那么C语言会隐式地把有符号参数强制类型转换为无符号，并假设这两个数都是非负的。
对于 这样的关系运算符来说，它会导致非直观的结果。我们同样用一个C语言程序来作为测试：

#include
#include
int main(void)
{
    printf("%d", -1 < 0U);
    printf("%d",(unsigned)-1 > -2);
}

VS2017运行结果：

第一个表达式中，由于0是无符号数，所以-1默认变成无符号数，即为2³²-1,这个数必然比0要大。所以第一个表达式为假。
第二个表达式中，通过把-1强制转换成无符号数，-1变为2³²-1，-2变为2³²-2，所以第二个表达式为真。

扩展一个数字的位表示

有时我们会把一个占用空间较小的数据类型转换为占用空间较大的数据类型(如果把占用空间较大的数据类型转换为占用空间较小的数据类型，可能会丢失数据，我们一般不推荐这么做)。

无符号数的零扩展

定义宽度为w位的位向量：

和宽度为w’的位向量：

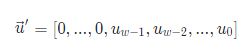
其中w'>w。则：

要将一个无符号数转换为一个更大的无符号数数据类型，我们只要简单的在前面加上足够的0即可，这种运算被称为零扩展。

有符号数的符号拓展

定义宽度为w位的位向量：

和宽度为w’的位向量：

其中w'>w。则：

要将补码数字转换为一个更大的数据类型，可以执行一个符号扩展(sign-extension)，在前面添加最高有效位的值。
具体证明略。

值得注意的点：在C语言中，把类型不同、大小不同的两个数据类型相互转换，先改变数据类型的大小，然后在执行类型转换。
比如说：在C语言中，把一个short类型的变量转换为unsigned类型的变量，我们要先把short类型的变量扩展到8个字节，然后再执行有符号数到无符号数的转换。

截断数字

一些特殊情况下，尽管这样做会带来风险，但我们仍然有时候会需要把一个高位的数据类转换为低位的数据类型，这时候我们就需要截断这个数字。

无符号数的截断

定义宽度为w位的位向量：

而它截断为k位的结果为：

令x=B2U_w(\vec x),x'=B2U_(\vec x'),则x'=x mod 2^k。
截断为k为实际上就是对原数的真值用2^k取模。具体证明过程略。

有符号数的截断

要理解有符号数的截断，我们首先要明白，无论是有符号数还是无符号数真正区别他们的不是他们的真值，而是他们的编码方式，实际上无论是有符号数，还是无符号数，在内存中都表示为串二进制数，有了编码对他们真值的解释，他们才能表示不同的数据。
我们都知道，截断实际上就是截去前面冗余的位，只留下我们需要的位，既然无符号数和有符号数在内存中表示的方法实际上都是一串二进制数，我们为什么不可以把一个有符号数的位模式，看做是无符号数的编码，用无符号数的方式将其截断后得到的真值，再用把无符号数转换为有符号数，最终得到将有符号数阶段的真值。
总而言之，有符号数编码的截断结果是: