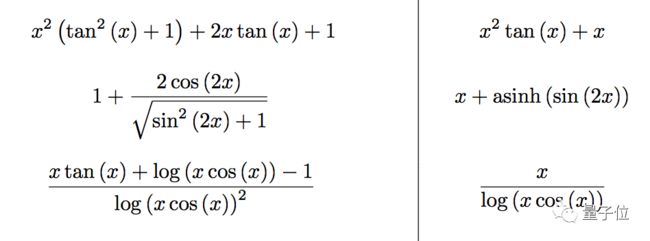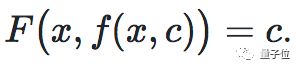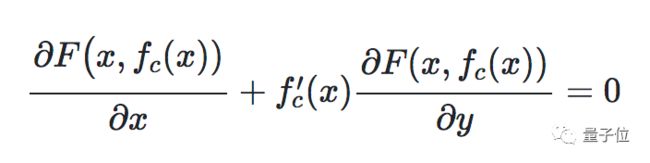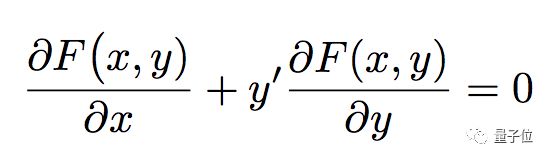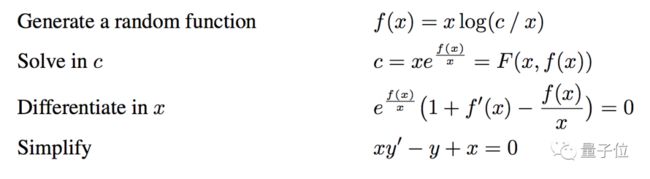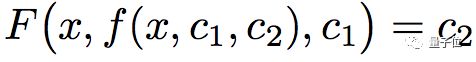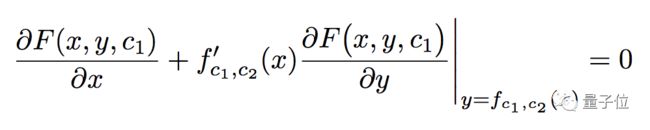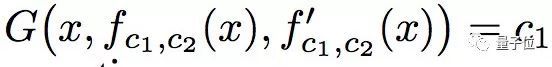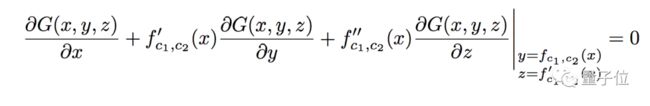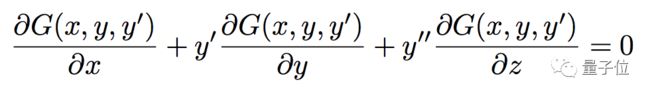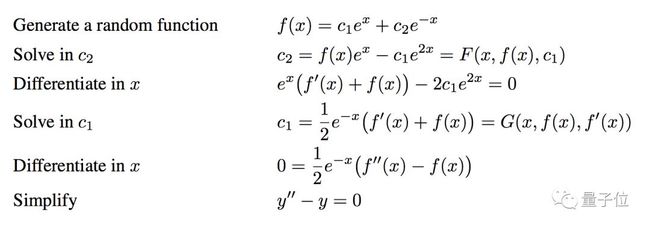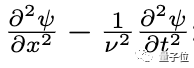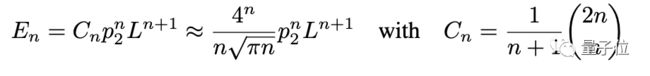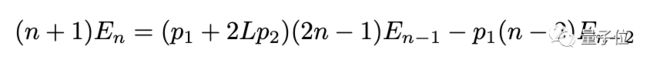AI攻破高数核心,1秒内精确求解微分方程、不定积分,性能远超Matlab
栗子 鱼羊 发自 海边边
量子位 报道 公众号 QbitAI
大家都知道,AI (神经网络) 连加减法这样的简单算术都做不好:
可现在,AI 已经懂得微积分,把魔爪伸向你最爱的高数了。
它不光会求不定积分:
还能解常微分方程:
一阶二阶都可以。
这是 Facebook 发表的新模型,1 秒给出的答案,超越了 Mathematica 和 Matlab 这两只付费数学软件 30 秒的成绩。
团队说,这是Seq2Seq和Transformer搭配食用的结果。
用自然语言处理 (NLP) 的方法来理解数学,果然行得通。
这项成果,已经在推特上获得了 1700 赞。许多小伙伴表示惊奇,比如:
感谢你们!在我原本的想象中,这完全是不可能的!
而且,据说算法很快就要开源了:
到时候让付费软件怎么办?
巨大数据集的生成姿势
要训练模型做微积分题目,最重要的前提就是要有大大大的数据集。
这里有,积分数据集和常微分方程数据集的制造方法:
函数,和它的积分
首先,就是要做出“一个函数&它的微分”这样的数据对。团队用了三种方法:
第一种是正向生成 (Fwd) ,指生成随机函数 (最多n个运算符) ,再用现成的工具求积分。把工具求不出的函数扔掉。
第二种是反向生成 (Bwd) ,指生成随机函数,再对函数求导。填补了第一种方法收集不到的一些函数,因为就算工具求不出积分,也一定可以求导。
第三种是用了分部积分的反向生成 (Ibp) 。前面的反向生成有个问题,就是不太可能覆盖到f(x)=x3sin (x)的积分:
F(x)=-x3cos (x) +3x2sin (x) +6xcos (x)-6sin (x)
因为这个函数太长了,随机生成很难做到。
另外,反向生成的产物,大多会是函数的积分比函数要短,正向生成则相反。
为了解决这个问题,团队用了分部积分:生成两个随机函数F和G,分别算出导数f和g。
如果 fG 已经出现在前两种方法得到的训练集里,它的积分就是已知,可以用来求出 Fg:
∫Fg=FG-∫fG
反过来也可以,如果 Fg 已经在训练集里,就用它的积分求出 fG。
每求出一个新函数的积分,就把它加入训练集。
如果 fG 和 Fg 都不在训练集里,就重新生成一对F和G。
如此一来,不借助外部的积分工具,也能轻松得到x10sin (x)这样的函数了。
一阶常微分方程,和它的解
从一个二元函数F(x,y)说起。
有个方程F(x,y)=c,可对y求解得到y=f(x,c)。就是说有一个二元函数f,对任意x和c都满足:
再对x求导,就得到一个微分方程:
fc表示从x到f(x,c)的映射,也就是这个微分方程的解。
这样,对于任何的常数c,fc都是一阶微分方程的解。
把fc替换回y,就有了整洁的微分方程:
这样一来,想做出“一阶常微分方程&解”的成对数据集,只要生成一个f(x,c),对c有解的那种,再找出它满足的微分方程F就可以了,比如:
二阶常微分方程,和它的解
二阶的原理,是从一阶那里扩展来的,只要把f(x,c)变成f(x,c1,c2) ,对c2有解。
微分方程F要满足:
把它对x求导,会得到:
fc1,c2表示,从x到f(x,c1,c2) 的映射。
如果这个方程对c1有解,就可以推出另外一个三元函数G,它对任意x都满足:
再对x求导,就会得到:
最后,整理出清爽的微分方程:
它的解就是fc1,c2。
至于生成过程,举个例子:
现在,求积分和求解微分方程两个训练集都有了。那么问题也来了,AI 要怎么理解这些复杂的式子,然后学会求解方法呢?
将数学视作自然语言
积分方程和微分方程,都可以视作将一个表达式转换为另一个表达式,研究人员认为,这是机器翻译的一个特殊实例,可以用 NLP 的方法来解决。
第一步,是将数学表达式以树的形式表示。
运算符和函数为内部节点,数字、常数和变量等为叶子节点。
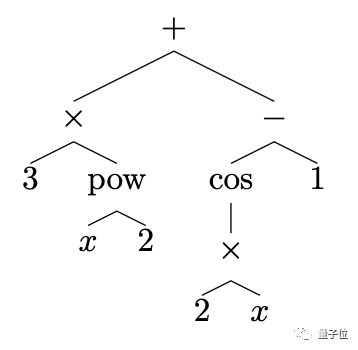
比如 3x^2 + cos (2x) - 1 就可以表示为:
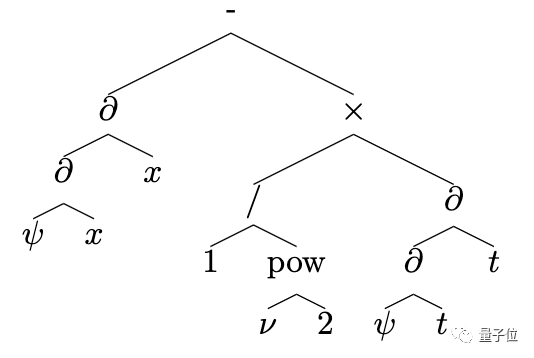
再举一个复杂一点的例子,这样一个偏微分表达式:
用树的形式表示,就是:
采用树的形式,就能消除运算顺序的歧义,照顾优先级和关联性,并且省去了括号。
在没有空格、标点符号、多余的括号这样的无意义符号的情况下,不同的表达式会生成不同的树。表达式和树之间是一一对应的。
第二步,引入 seq2seq 模型。
seq2seq 模型具有两种重要特性:
输入和输出序列都可以具有任意长度,并且长度可以不同。
输入序列和输出序列中的字词不需要一一对应。
因此,seq2seq 模型非常适合求解微积分的问题。
使用 seq2seq 模型生成树,首先,要将树映射到序列。
使用前缀表示法,将每个父节点写在其子节点之前,从左至右列出。
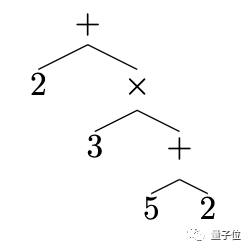
比如 2 + 3 * (5 + 2),表示为树是:
表示为序列就是 [+ 2 * 3 + 5 2]。
树和前缀序列之间也是一一映射的。
第三步,生成随机表达式。
要创建训练数据,就需要生成随机数学表达式。前文已经介绍了数据集的生成策略,这里着重讲一下生成随机表达式的算法。
使用n个内部节点对表达式进行统一采样并非易事。比如递归这样的方法,就会倾向于生成深树而非宽树,偏左树而非偏右树,实际上是无法以相同的概率生成不同种类的树的。
所以,以随机二叉树为例,具体的方法是:从一个空的根节点开始,在每一步中确定下一个内部节点在空节点中的位置。重复进行直到所有内部节点都被分配为止。
不过,在通常情况下,数学表达式树不一定是二叉树,内部节点可能只有 1 个子节点。如此,就要考虑根节点和下一内部节点参数数量的二维概率分布,记作 L (e,n)。
接下来,就是对随机树进行采样,从可能的运算符和整数、变量、常量列表中随机选择内部节点及叶子节点来对树进行“装饰”。
最后,计算表达式的数量。
经由前面的步骤,可以看出,表达式实际上是由一组有限的变量、常量、整数和一系列运算符组成的。
于是,问题可以概括成:
- 最多包含n个内部节点的树
- 一组p1个一元运算符(如 cos,sin,exp,log)
- 一组p2个二进制运算符(如+,-,×,pow)
- 一组L个叶子值,其中包含变量(如x,y,z),常量(如e,π),整数(如 {-10,…,10})
如果p1 = 0,则表达式用二叉树表示。
这样,具有n个内部节点的二叉树恰好具有 n + 1 个叶子节点。每个节点和叶子可以分别取p1和L个不同的值。
具有n个二进制运算符的表达式数量就可以表示为:
如果p1 > 0,表达式数量则为:
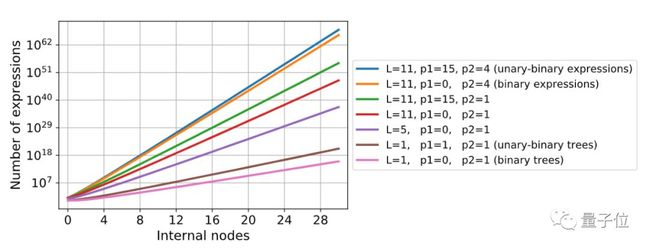
可以观察到,叶子节点和二元运算符的数量会明显影响问题空间的大小。
胜过商业软件
实验中,研究人员训练 seq2seq 模型预测给定问题的解决方案。采用的模型,是 8 个注意力头(attention head),6 层,512 维的 Transformer 模型。
研究人员在一个拥有 5000 个方程的数据集中,对模型求解微积分方程的准确率进行了评估。
结果表明,对于微分方程,波束搜索解码能大大提高模型的准确率。
而与最先进的商业科学计算软件相比,新模型不仅更快,准确率也更高。
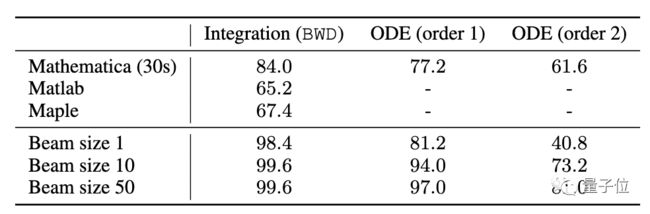
在包含 500 个方程的测试集上,商业软件中表现最好的是 Mathematica。
比如,在一阶微分方程中,与使用贪婪搜索解码算法(集束大小为1)的新模型相比,Mathematica 不落下风,但新方法通常 1 秒以内就能解完方程,Mathematica 的解题时间要长的多(限制时间 30s,若超过 30s 则视作没有得到解)。
而当新方法进行大小为 50 的波束搜索时,模型准确率就从 81.2% 提升到了 97%,远胜于 Mathematica(77.2%)
并且,在某一些 Mathematica 和 Matlab 无力解决的问题上,新模型都给出了有效解。
邀请 AI 参加 IMO
这个会解微积分的 AI 一登场,就吸引了众多网友的目光,引发热烈讨论。网友们纷纷称赞:鹅妹子嘤。
有网友这样说道:
这篇论文超级有趣的地方在于,它有可能解决复杂度比积分要高得高得高得多的问题。
还有网友认为,这项研究太酷了,该模型能够归纳和整合一些 sympy 无法实现的功能。
不过,也有网友认为,在与 Mathematica 的对比上,研究人员的实验设定显得不够严谨。
默认设置下,Mathematica 是在复数域中进行计算的,这会增加其操作的难度。但作者把包含复数系数的表达式视作“无效”。所以他们在使用 Mathematica 的时候将设置调整为实数域了?
我很好奇 Mathematica 是否可以解决该系统无法解决的问题。
30s 的限制时间对于计算机代数系统有点武断了。
但总之,面对越来越机智的 AI,已经有人发起了挑战赛,邀请 AI 挑战 IMO 金牌。
Facebook AI 研究院出品
这篇论文有两位共同一作。
Guillaume Lample,来自法国布雷斯特,是 Facebook AI 研究院、皮埃尔和玛丽·居里大学在读博士。
他曾于巴黎综合理工学院和 CMU 分别获得数学与计算机科学和人工智能硕士学位。2014 年进入 Facebook 实习。
François Charton,Facebook AI 研究院的客座企业家(Visiting entrepreneur),主要研究方向是数学和因果关系。
传送门
https://arxiv.org/abs/1912.01412
https://news.ycombinator.com/item?id=21084748