机器学习当中的数学---微分学部分
关于无穷小的物理学遐想
我认为无穷小还是很不好理解的,于是我想到了物理学上的另外一个类比,也就是牛顿的经典力学和爱因斯坦的相对论。
无穷小的自然语言解释是,当自变量x趋向于0的时候,函数。但是不同函数趋于0的速度是不同的,最典型的就是指数型的函数比如就要比趋于0的速度要快很多,因此是的高阶无穷小,记作,相应的其他函数的类比也是一样的。
无穷小与无穷小的比较
如果一个无穷小是另外一个无穷小的高阶无穷小,那么两者之比就是0。
其实两个无穷小可以认为是两个维度或者说两个世界的东西,实际上算术上的差距并没有可比性,就好像我们在牛顿经典力学时空观下,我们的运动其实是相对于光速的极限下是静止不动的一样,这里也就是相当于那个与的比较一样,要比小得太多太多太多了,以至于在这个无穷小看来看来也是0。正如光速比我们快得太多太多太多了,实际上那个与,光与我们已经不是同一个维度下的东西了,我们无法理解光在那种速度下会发生什么事。而同阶无穷小,就像光与其他电磁波一样,虽然它们快得难以被我们理解,但他们是同样地快,或者说他们的速度的差别是可以被测量,被常数化的,所以其实是相同的级别。
当x较小的时候
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
%matplotlib inline
import seaborn as sns
plt.style.use('ggplot')
x=np.linspace(0,20,9)
y=2*x**2+2*x+1
new_x=[i for i in x if x.tolist().index(i)%2==0]
new_y=2*np.array(new_x)**2+2*np.array(new_x)+1
在做任何事情前,一定要明白为什么这么做。这也是为什么学习机器学习要从学习高等数学开始,这点很重要。
因为机器学习本质上是一个逼近的问题,我们现在可以回到欧几里得时代,发现圆的测量可能没有工具借助,几乎是不可能的,但是聪明的哲学家或者说研究者,他们通过对圆进行外接和内接,通过求圆内部和外部的多边形的面积,如果不断增加边的数量,那么外接和内接多边形就可以不断逼近圆,最终三者的面积的极限就是相等的,进而求出圆的面积
fig=plt.figure(figsize=(8,8))
ax=fig.add_subplot(1,1,1)
circle1=plt.Circle((0.5, 0.5), 0.2, color='k', fill=False)
ax.add_artist(circle1)
import matplotlib.pyplot as plt
from matplotlib.patches import CirclePolygon
circle = CirclePolygon((0, 0), radius = 0.75, fc = 'y')
plt.gca().add_patch(circle)
verts = circle.get_path().vertices
trans = circle.get_patch_transform()
points = trans.transform(verts)
# print(points)
plt.plot(points[:,0],points[:,1])
plt.axis('scaled')
plt.show()
机器学习当中的逼近
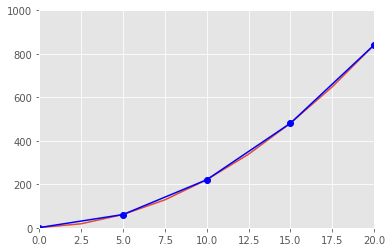
低阶的线性逼近
plt.plot(x.tolist(),y.tolist())
plt.plot(new_x, new_y, 'b-o')
plt.xlim(0,20)
plt.ylim(0,1000)
plt.show()
fig=plt.figure(figsize=(16,8))
x_s=np.linspace(1,10000,1000)
y_s=np.sin(2*np.pi*x_s)
x_s_new=np.array([i for i in x_s if x_s.tolist().index(i)%20 == 0])
y_s_new=np.sin(2*np.pi*x_s_new)
plt.plot(x_s, y_s)
plt.plot(x_s_new, y_s_new,'b--o')
[]
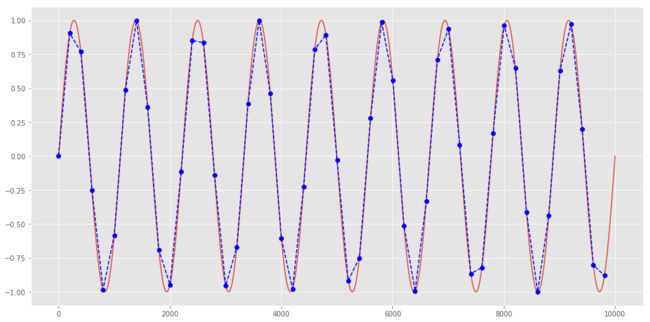
从上面看到,都是用一些局部的线性函数去逼近一些复杂的函数,这样子我们就可以用简单的函数去近似出复杂的函数,可以想到,如果点足够多的话可以无限逼近。线性方程在该点的值与该复杂函数在该点的值是一致的。
这里的是的高阶无穷小,也就是,相当于横坐标差,当的时候,因为是的高阶无穷小,因此趋于0的速度要快于前面的线性方程部分,因此。
也就是复杂函数和线性方程逼近于的这个极限是相同的,在非趋近的情况下是个误差项
高阶的线性逼近
上面的是低阶的线性逼近,这里的“低阶”意思是指只有次数为1的导数,我们可以想到后面的导数部分又可以展开,所以
进行进一步的展开,这里进行二阶的泰勒展开后误差为的高阶无穷小,如果是n阶展开的话就是n阶无穷小
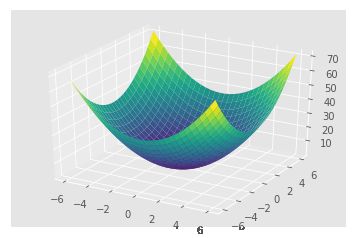
多元函数的逼近
from mpl_toolkits import mplot3d
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return x ** 2 + y ** 2
x = np.linspace(-6, 6, 30)
y = np.linspace(-6, 6, 30)
X, Y = np.meshgrid(x, y)
# print(X)
Z = f(X, Y)
Z.shape
(30, 30)
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
cmap='viridis', edgecolor='none')
plt.show()
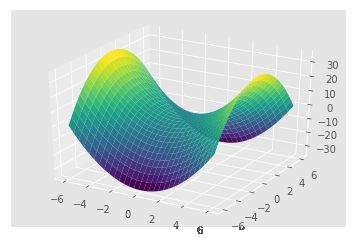
多元函数
偏导数
其实偏导数就是,对于一个多元函数,比如说二元函数f(x,y)其沿着坐标轴方向上的导数即为偏导数,沿着x方向上的为x的偏导数,在y方向为y的偏导数。表示为:
以上是沿着x轴和y轴方向上的偏导数,如果是沿着任意一个方向的话,在该方向上该多元函数的导数为
和可以认为是在x轴和y轴方向的一个投影,从x和y的方向上进行逼近。
线性逼近
同样的,类似于一元复杂函数可以通过一个线性函数来不断逼近,多元函数也可以用一个线性方程来不断逼近
偏导数与梯度的关系
我们上面说过,偏导数是多元函数对于x轴和y轴方向上的导数,但是很多时候我们并不是只限定在x轴和y轴方向上求导数,比如v方向,,那么在v方向上的导数不叫偏导数,叫梯度,梯度也是在该点处下降最快的方向。
我们将某点(x, y)x轴的偏导数和y轴的偏导数组成一个向量,表示为(备注:T表示为列向量的意思)
那么在该点(x, y)朝着某个方向最快下降方向也就是梯度方向,表示为
关于导数为什么是下降最快的方向
import seaborn as sns
# def f(x):
# return np.sin(2*np.pi * x)
# x_d=np.linspace(0, 1000, 500)
# y_d=f(x_d)
# x_p=x_d[250]
# y_p=np.sin(2*np.pi * x_p)
# f_der=2*np.pi*np.cos(2*np.pi*x_p)#get the derivatives
# print(f_der)
# tangent_line=y_p+f_der*(x_d-x_p)
# plt.plot(x_d,y_d,'-b',x_p, y_p, 'om', x_d, tangent_line,'--r')
# # plt.plot(x_d,y_d)
# plt.xticks(color='w')
# plt.yticks(color='w')
# plt.ylim(-1,1)
# plt.show()
def f(x): # sample function
return x*np.sin(np.power(x,2))
# evaluation of the function
x = np.linspace(-2,4,150)
y = f(x)
a = 1.4
h = 0.1
fprime = (f(a+h)-f(a))/h # derivative
tan = f(a)+fprime*(x-a) # tangent
larger_tan = f(a)+ -5*(x-a) # larger tangent
print(fprime)
# plot of the function and the tangent
plt.plot(x,y,'b',a,f(a),'om',x,tan,'--r',x,larger_tan, '-g')
plt.xticks(color='white')
plt.yticks(color='white')
plt.show()
-1.2818633377155364
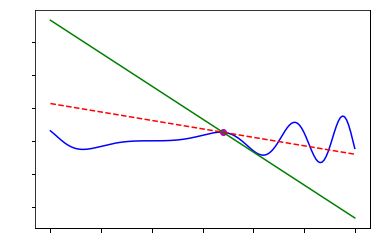
关于这个问题,我的理解是这样的,在图上那个红点处,红色虚线是切线,绿色是绝对值大于切线斜率绝对值的线,我们想象成一个点在曲线上快速运动,它不能越轨,否则该点就不算是曲线上的点了,这样的话,每个点在曲线上面的最大下降方向只能是切线方向,如果比切线下降更快,如绿色线,接下来这个点继续往绿色方向运动,哪怕一点点,都是飞出图上蓝色的轨道外了,也就不算是曲线上的点了。所以在某一点处,切线方向一定是下降最快的方向
梯度下降法和牛顿法
简而言之,梯度下降法就是多元函数的线性逼近,而牛顿法相当于是多元函数泰勒展开后的n阶逼近。(不太明白的可以参考一元函数的线性逼近和n阶逼近)
先修知识 泰勒展开
泰勒展开是关于某个复杂函数在a点处的展开表达式,对于一个无限可微分函数,其在真实点处的泰勒展开式为
梯度下降法
梯度下降法相当于是对函数在这点的线性逼近
梯度下降法并不能告诉我们极小值点在哪,但是可以告诉我们在这一点下降最快的方向在哪里。然后我们可以以一定的下降速率去更新已有的值。这个下降速率就是学习率,类似于一个人在完全黑暗之中在山谷里面摸索最低点谷底,那么学习率就像是这个人的步伐,可以一脚迈一大步,但是很容易迈过头;同样,也可以一脚迈一小步,但收敛速度会很慢。
对于一个数据集X来说,其梯度就是所有单个样本的梯度之和
其中是指样本i,i从1到n代表X所有的每个样本,而则代表样本i的梯度
梯度下降根据对总体样本的选取不同计算出选取样本的梯度,以此样本计算出来的梯度作为参数更新的方向,直到梯度为0的时候即为到达最优点。三种不同的计算梯度方式:
- 全量梯度下降法
这种方法就是计算所有样本的梯度之和,以此作为参数更新的方向
- 随机梯度下降法
这种方法是每次只计算一个样本的梯度,以此作为参数更新的方向,一般配合学习率逐渐降低的方法,有和全量梯度相似的收敛速度,好处是可以跳出局部最优点,有可能找到全局最优点
- 小批量随机梯度下降法
这种方法也是随机抽取样本,不同的是,每次计算梯度是以每个小样本的梯度之和作为更新方向,比起随机梯度下降法来说好处是更加容易收敛,受单个样本波动性更小。
def plot_saddle(x, y):
return x**2 - y**2
from mpl_toolkits import mplot3d
from mpl_toolkits.mplot3d import Axes3D
Z2=plot_saddle(X, Y)
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z2, rstride=1, cstride=1,
cmap='viridis', edgecolor='none')
plt.show()
plt.contour(X, Y, Z2, 20, cmap='RdGy');
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
cmap='viridis', edgecolor='none')
plt.show()
plt.contour(X, Y, Z, 20, cmap='RdGy');
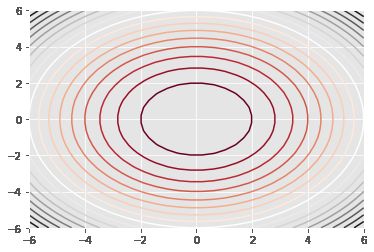
如何阅读等高线图:
- 等高线越密集的地方,说明其斜度越大。
- 等高线包围的一圈又一圈可能是valley,可能是mountain,需要通过等高线的密集变化来看出。
- 从上面可以看出来,对于低谷来说,其两侧的等高线由外向内梯度越来越小,对于山谷则刚好相反,其梯度越来越大,参考再上面一副图的左右两边,鞍形的左右两边就各是一座山峰,中间等高线变缓的就是鞍部。
牛顿法
首先要明白牛顿法是做什么的,它是要找到时候的x值
牛顿法与初始点的选取很有关系,如果初始点所对应的切线斜率为0的话,那么接下来的x值就无法更新。牛顿法的好处是,比起一阶的梯度下降,其收敛速度会更快。
参考链接:https://blog.paperspace.com/intro-to-optimization-momentum-rmsprop-adam/
这个二阶导数是多个变量的求导组合,其形式如下:
对于两个变量的情况:
这里的第一行代表先对进行求导,再依次对,进行二阶求导,同理第二行也是一样的对进行相同的操作。
对于多个变量则有:
牛顿法一个很好地弥补了一阶的梯度下降的缺点,一阶的梯度下降只能知道当前函数值是下降还是上升以及斜率的绝对值,但并不知道当前下降的快慢,也就是不知道目前是否已经越来越陡还是越来越缓,而二阶导数可以弥补这个问题
打个比方,就好像如果我们只有一阶的信息,那么我们能知道身处现在的位置,往哪个方向上是下降的,而且下降得最快,但我们并不知道接下来越来越缓还是越来越陡
牛顿法对多元函数的二阶求导
def newton_func(x):
return x**2 + 2 * x -3
fig=plt.figure()
x_r=np.linspace(-5,1, 600)
y_r= newton_func(x_r)
x_rp=-3
y_rp=0
x_rp2=1
y_rp2=0
plt.plot(x_r, y_r, 'r--', x_rp, y_rp, 'om',x_rp2, y_rp2,'om')
plt.text(x_rp+0.2, y_rp+0.5, 'a')
plt.text(x_rp2+0.1, y_rp2+0.5, 'b')
plt.hlines(y=0,xmin=-5,xmax=1)
plt.xticks(color='w')
plt.yticks(color='w')
(array([-6., -4., -2., 0., 2., 4., 6., 8., 10., 12., 14.]),
)
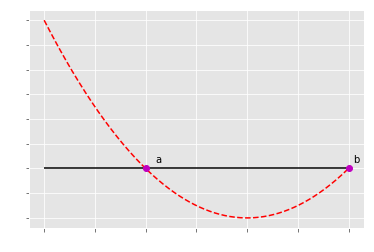
比如在这里有个函数,那么牛顿法的目的就是要求出等于0的时候的x值,也就是a点和b点的对应的x(在图中就是-3和-1)
x_rp3=-4.8
y_rp3=newton_func(x_rp3)
h = 0.1
fprime = (newton_func(x_rp3+h)-newton_func(x_rp3))/h # derivative
xrange=np.linspace(-5, -3, 600)
tan = newton_func(x_rp3)+fprime*(xrange-x_rp3) # tangent
# larger_tan = f(x_rp3)+ -5*(x-x_rp3) # larger tangent
plt.plot(x_r, y_r, 'r--', x_rp, y_rp, 'om',x_rp2, y_rp2,'om',x_rp3, y_rp3,'om', xrange, tan, 'g--')
plt.text(x_rp+0.2, y_rp+0.5, 'a')
plt.text(x_rp2+0.1, y_rp2+0.5, 'b')
plt.text(x_rp3+0.1, y_rp3+0.5, 'c')
plt.hlines(y=0,xmin=-5,xmax=1)
plt.vlines(x=x_rp3,ymin=-4, ymax=12,linestyles='dashed',color='blue')
plt.xticks(color='w')
plt.yticks(color='w')
(array([-6., -4., -2., 0., 2., 4., 6., 8., 10., 12., 14.]),
)
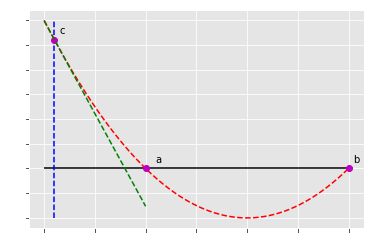
牛顿法就是通过不断更新某个点的切线与x轴相交的点,从而不断逼近f(x)=0时候的x值
比如我们选c点(x1, y1)作为起始点,做切线,跟x轴会有交点,这个时候这个交点对应的x在曲线上面的点为x2,这个时候x2比x1接近了a点,继续做(x2, y2)的切线,重复以上的步骤,直到找到xn对应的f(x_n)无限接近于0,x_n无限接近于a点的横坐标,这就是牛顿法。而在求损失函数的时候我们想要找到一阶导数为0的,用的函数是一阶导数,而对应的切线斜率则是二阶导数
关于梯度下降法和牛顿法的直观区别
关于梯度下降法,我认为一个直观的解释就是,像是下山的时候总是在每走一步就看一下周围,朝着下降最快的方向进行更新,直到梯度为0,那么就不再更新,因为。
对于牛顿法,它的目标则不一样,它是通过二阶梯度来不断以当前点x以及梯度来计算出当前点的切线与x轴的交点,这个交点越来越逼近于极小值点,直到梯度无限接近于0,更新的方式是。在这个过程中,二阶梯度其实可以描绘出一阶梯度的变化,也就是山的斜率是越来越陡还是越来越缓,从而相应地去调节学习率(每次的更新的步伐大小),而一阶梯度相对于二阶梯度,它只能告诉我们现在是下山还是上山,这个坡的斜率是多少(有多陡),而并不能告诉我们是越来越缓,还是越来越陡,自然也就无法自适应学习率了。
为什么机器学习中不多使用牛顿法
主要是因为牛顿法要求二阶导数,而对于多个变量来说,求二阶导数是一个交叉组合的形式,比如对于两个变量, 其函数的二阶梯度是一个的矩阵,而n个则是,对于有多个特征的情况下,这种计算是指数型地增长
动量法
参考链接:https://towardsdatascience.com/stochastic-gradient-descent-with-momentum-a84097641a5d
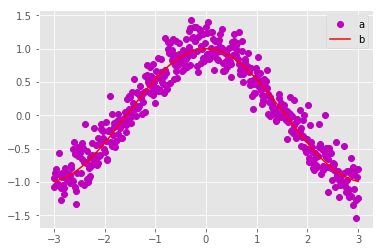
动量法的出现其实是因为数据点有很多噪音,我们希望能够让权重在通过这些数据点计算出损失函数梯度下降的时候能够把握好大方向,而减少噪声对梯度更新方向的干扰。
动量法的梯度更新方式如下:
t代表在数据点t的时候,代表对前面的t-1个数据点进行动量法更新后的序列,是原始的数据点,相当于每次更新的时候都会保留之前的余势,这样可以减少单个数据点的噪声的影响。
def cos(x):
return np.cos(x)
np.random.randn()
y_noi
array([-2.49084187, -2.44073906, -2.35054648, -2.22411117, -2.06682606,
-1.88539995, -1.68757134, -1.48177834, -1.27679879, -1.08137583,
-0.90384497, -0.75177856, -0.63166279, -0.54862105, -0.50619538,
-0.50619538, -0.54862105, -0.63166279, -0.75177856, -0.90384497,
-1.08137583, -1.27679879, -1.48177834, -1.68757134, -1.88539995,
-2.06682606, -2.22411117, -2.35054648, -2.44073906, -2.49084187])
x_noi=np.linspace(-3, 3, 500)
y_noi=cos(x_noi) + np.random.randn(len(x_noi))*0.2
plt.plot(x_noi, y_noi, 'om', x_noi,cos(x_noi),'-r')
plt.legend(['a','b'])
计算前面原始序列的加和
y_t = 0
s_t=[]
for i in range(len(y_noi)):
y_t = y_t + y_noi[i]
s_t.append(y_t)
计算平均后的序列
v_t = 0
v_new = []
for i in range(len(y_noi)):
v_t = 0.9 * v_t + (1 - 0.9) * y_noi[i]
v_new.append(v_t)
def plot_beta(beta):
v_t = 0
v_new = []
for i in range(len(y_noi)):
v_t = beta * v_t + (1 - beta) * y_noi[i]
v_new.append(v_t)
return v_new
plt.figure(figsize=(10, 5))
x_noi=np.linspace(-3, 3, 500)
y_noi=cos(x_noi) + np.random.randn(len(x_noi))*0.2
plt.plot(x_noi, y_noi, 'om', x_noi,cos(x_noi),'-r')
plt.plot(x_noi,plot_beta(0.5), color='green', marker='o', linewidth=2)
plt.plot(x_noi,plot_beta(0.9), color='blue', marker='o', linewidth=2)
plt.plot(x_noi,plot_beta(0.98), color='yellow', marker='o', linewidth=2)
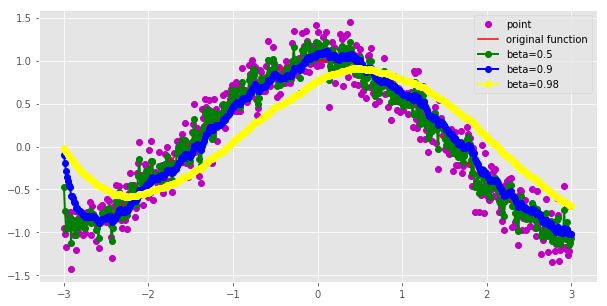
plt.legend(['point', 'original function', 'beta=0.5', 'beta=0.9', 'beta=0.98'], loc='upper right')
plt.show()
如图是对不同beta进行求和的结果,动量法在每次更新梯度的的时候都有两部分组成,一个是前面的余量,也就是,beta从直觉上来说可以认为是在计算梯度更新的时候对前面数据点的余势的权重,而则是对当前数据点的权重,因此减少了单个数据点对梯度更新方向的波动的影响,变得更加稳健,从上面可以看出来,随着值越来越大,曲线越来越光滑,但是会有偏移。
在损失函数的更新公式当中表现为:
总体上看,既保留了前面数据点的余势(也就是它们的梯度,包括方向和大小),另外一方面也有当前点的梯度。由这两部分组成。物理上看像是推动一个很重的铁球下山,因为铁球保持了下山的方向,所以铁球向左右两侧的振荡会越来越少,两侧就是非函数方向,也就是噪声。
Nesterov accelerated gradient(动量法的改进算法)
动量法的问题在于随着后面的不断叠加,余势会越来越大,那么我们希望当损失函数的梯度接近于0的时候,能够减小学习率。要做到这一点,我们可以通过使用下一步的损失函数梯度。公式如下:
这样可以提早预知下一步的梯度,从而尽早进行刹车,也就是减小步伐,减小学习率。
Adagrad算法
Adagrad是一种自动调整学习率的办法,这种调整包括对于每一步的学习率,以及不同参数的学习率都不同:
- 随着模型的训练,学习率会逐渐衰减。
- 对于更新参数比较频繁的变量,学习率会比较大。
- 对于更新参数比较缓慢的变量,学习率比较小。
实现原理
这里实现原理主要是从历史上的更新梯度叠加组合成一个历史梯度的矩阵,并取对角线上面的组合值作为下一次更新的惩罚参数。
梯度:
梯度历史矩阵:
为对角矩阵,上面的元素
参数更新:
在这里i是代表第几个特征,t是代表第t次更新,对角矩阵上面的元素是前面到现在的梯度的叠加,如果叠加越多,相应学习率就会越小,更新也会放慢
AdaDelta(Adagrad的改进算法)
AdaDelta解决了Adagrad学习率衰减过快的问题,因为分母一直都是前面的累加,AdaDelta则是将分母从前面的历史梯度的全部累加改成了历史的移动平均值。
同时之前说的Adagrad和其他梯度算法没有解决一个问题是参数的单位和梯度的单位并不是一致的,因此AdaDelta进一步把学习率改成了前面的参数更新的移动平均值。更新后结果如下:
Adam(基于AdaDelta进行改进的算法)
AdaDelta是对二阶矩(也就是下面的梯度的平方求移动平均值),而Adam则是更进一步,对也进行一阶的求移动平均值。更新公式如下:
结论
究竟如何选择算法呢?
• 动量法与Nesterov的改进方法着重解决目标函数图像崎岖的问题
• Adagrad与Adadelta主要解决学习率更新的问题
• Adam集中了前述两种做法的主要优点