今天回顾了一下检索部分的内容,写在这里和大家分享,有错误的地方请不吝指正。(挑一些觉得重要的点讲)
1、 考虑在线性表和散列表上的检索
2、 用ASL来表示检索的平均效率,要考虑失败和成功两种可能
3、 基于线性表的检索:
1) 顺序检索:对于一个有n元素的线性表,成功为, 失败为(设置了一个监视哨),平均为
2) 二分检索:前提条件是线性表有序,复杂度为,伪代码:
def binarysearch(L, s, e, key):
while s <= e:
mid = (s + e) // 2
if L[mid] < key:
s = mid + 1
elif L[mid] > key:
e = mid - 1
else:
return mid
return -1
要注意的一个问题是,对于一个长度为n的线性表,失败的检索长度为的上取整或者下取整,可以自己画图看一下;成功的检索平均长度也是在这个量级,自己估计,注意求和的方法,缺点是不易更新且要排序
3) 分块检索:块内无序,块间有块(前一个块的最大值<后一个块的最小值)
需要一个索引表(存每个块的最大值,下标,对应块中元素个数)来辅助查找,设有b个块,每个块平均s个元素,若全部都是用顺序查找的话,b = s = sqrt(n)的时候效率最高,ASL = sqrt(n),不难发现缺陷。
4、 散列表:从数组寻址找到的灵感,从要寻找的关键码直接对应到地址。负载因子a = N/M,一般来说a的范围是[0,1](开散列其实不受限制),问题:如何“散列”、如何解决冲突。
5、 直接求余数法、乘余取整法、平方取中法、数字分析法(考虑某一位的分布均匀性,取出若干位分布均匀的作为地址)、基数转换法、折叠法
6、 冲突解决方法:开散列(负载因子不受限制,但一般也是0~1)/闭散列
7、 开散列比较适用于记录可以存在内存的情况,因为如果存在外存且使用拉链法的话,有同义词的话可能会存在不同的磁盘页里导致I/O次数变大。所以用桶散列的方法来解决相关的外存问题。但是开散列中,拉链法适合不定长的情况,而且删除方法比较容易实现
8、 闭散列中,设关键码为k, 则h(k)为基地址,p(k,i)表示第i次查探的地址偏移量
di = d0 + i * p(k,i) 表示查找序列中的第i个地址
9、 对于p(k,i)取不同的函数有线性探查法、改进的线性探查(i*c)、二次探查法、伪随机探查法。
10、基本聚集:基地址不同的关键码的探查序列重叠在一起(用二次探查法或者伪随机可以较好的解决);二次聚集:基地址相同的关键码的探查序列重叠在一起(因为探查序列只是基地址的函数,和关键码无关)。
11、为了解决二次聚集的情况,考虑用双散列方法,也就是让探查序列变成与关键码有关的函数。用h1(key)生成基地址,h2(key)表示每次要跳过的常数项记录,h2(key)必须和模数M互素,计算量比较大,但是冲突少。
12、自己编写一个数据结构来实现哈希表的功能。
插入:若探查序列中当前项不是空,如果等于待插入记录就返回false(不允许相同记录存在),否则就找下一个记录直到一个空的位置插入。
查找:比较简单,略去
删除:不能真正的删除,要考虑到这个位置可能在其他的探查序列里面,所以要分开记录“已删除”、“已占用”、“空”这三种状态,“已删除”的记录可以用来插入和查找、“空”的记录可以用来插入、“已占用”的记录可以用来“查找”、“删除”。
我们可以用一个“墓碑”来表示被删除的记录位置,删除的算法没有太大变化,但是在插入中要小心:由于不能重复插入记录,所以我们碰到墓碑时先记录下第一个待插入的墓碑,再检查后面的记录有没有出现相同记录,当然也可能插入在空的位置。伪代码如下:
def tomb_insert(e):
i = insplace = 0, pos = home = h(getkey(e))
tomb_pos = False
while !eq(EMPTY, HT[pos]):
if eq(e, HT[pos]):
return False #出现了相同记录,不插入
elif eq(tomb, HT[pos]) and !tomb_pos:
tomb_pos = True
insplace = pos
i += 1
pos = (home + p(getkey(e), i)) % M
if tomb_pos == False:
insplace = pos
HT[insplace] = e
return True
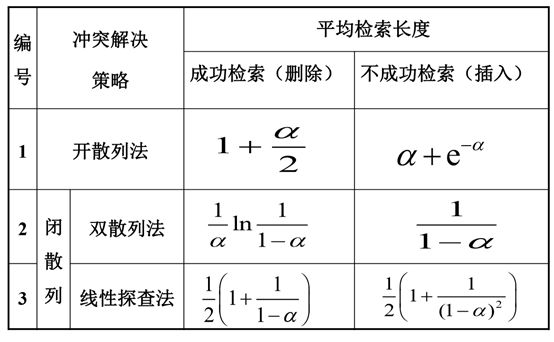
13、关于散列效率的分析,见下表:具体推导见算法导论(如果有时间看就尽力补上)
14、散列方法在负载因子大约为0.5时效率比较高,大于这个临界值时效率会急剧下降