翻译:王成林(麦克斯韦的麦斯威尔)审校:黄秀美(厚德载物)
大家好,你们能听到我讲话吗?这个演讲的内容是介绍RNG(随机数字生成)的一些黑暗秘密。如你在大屏幕上看到的,Squirrel已经介绍了一些RNG的基础概念。
首先,我想详细讲解几点。他的演讲更偏重理论,而我的更偏重实际应用一些,不仅仅会讨论一些在游戏开发中遇到的RNG相关的潜在的问题,还会介绍解决这些问题的工具。这个题目“黑暗秘密”不太好,会让人以为Squirrel探讨了黑暗的、复杂的数学公式,不过我们的重点是谈论如何使用那些数学公式。
首先我是谁?为什么你们要听我的演讲呢?这些是我参与制作的游戏。
有很多!在一些大工作室,我参与了《炉石传说》的制作,设计了游戏的一些原型,这是我制作的最好的一款游戏了。我只在那里工作了一年,当然是制作CCG(交换卡牌游戏),其中有很多随机数字生成。我独立开发过很多游戏,比如右下角的《Overland》,是一款roguelike类型游戏,其中有很多随机生成的关卡。现在我在Direwolf工作,位于科罗拉多州的丹佛市,我仍然负责开发CCG。也许以后会在这干下去,也许不会。
不过我们来谈谈使用RNG吧。我们从一些基础的、作为一名程序员在这个领域必须要面对的问题决策开始。这款解谜游戏《Connectrode》是我之前在2011年制作的,我的妻子非常喜欢,试玩了这款游戏的未成品。
这款俄罗斯方块风格的游戏会随机生成一些方块。有一天晚上我的妻子向我抱怨道:在一行中出现了9个颜色相同的方块!我意识到我需要修复这个bug。我采用俄罗斯方块游戏所使用的方法,有时人们将这个方法称为套袋方法(Bagging)。
这是用来为你的游戏加入随机性的一个基础方法。如果你像我一样每一轮都投掷一次骰子来从6个数字中随机得到一个数字,你会得到一个均匀分布。不过有的时候你不希望这个随机性过于随机,一个简单的方法是——这其实是一个设计决定,或者桌游设计者会这样说——“这里不应该使用骰子,而应该使用一副纸牌。”从数学上来讲,投骰子是对一个随机集合进行取样,允许样本的重复,取样不会改变该集合;而使用纸牌的话,你从中抽出一张牌后这张牌不会回到牌组中。
这样可以确保在分布中不会产生重复的结果。多数使用套袋方法的游戏都有一个套袋,套袋中包含一个随机集合。考虑纸牌的洗牌。我们可以使用三副纸牌洗牌——实际上拉斯维加斯的赌场现在就是这样做的,为了防止人们在黑杰克21点游戏中作弊。他们把三副或者更多副纸牌混在一起洗牌,这样会改变纸牌分布的随机性。因此如果你发现相同的分布规律一次又一次地出现,那么你要重点考虑一下它,这种情况对我来讲并不常见,不过你应该使分布更加平稳。另外我们还要考虑边缘情况。如果你同时洗三副牌,然后当没有牌的时候重新洗牌,首先你会想到你能得到的最大组合是三个黑桃尖。接着如果你重新对一副新牌洗牌,这时会产生一种边缘情况——字面意义上的边缘情况,即在一个套袋的末尾你有可能得到三个黑桃尖,而在另一个套袋的开始你又得到了三个黑桃尖。
这个边缘情况作为随机性的一个特殊情况值得考虑,因为这是RNG的第一个黑暗秘密:如果你没有提前计划使其不可能发生,那么每个随机的边缘情况可以发生,(最终!)将会发生在一个玩家上。
作为一名游戏程序员,你是确保这个问题不发生的最后一道防线,有的时候你要和设计师一起解决这个问题。我在Direwolf的这些CCG设计师同事,他们非常擅长数学。不过我也有和一些擅长美术的设计师工作过,他们的数学应用能力这方面很糟糕,所以有的时候程序员要站出来说“你考虑过这些了吗?”即使这通常是设计师的工作。
这里我引用了话剧《Rosencrantz and Guildenstern Are Dead》,其中的角色在整部剧中不断地投掷硬币,每次都是正面。这个概率非常小,不过在游戏中有的玩家有可能会掷出100次坏点。如果在数学上可能,那么最终一定会发生。你要把这点考虑进去。而这个问题的解决方法就是……这是暴雪的开发者发表的一篇蓝帖,介绍了《暗黑破坏神3》使用的方法,对于这种打装备的游戏来说,这个问题的解决非常重要。他们加入了一个我称之为“保底机制(Pity Timer)”的东西。
这里的蓝字解释道:“掉装备的概率很低。而对于有的玩家总也打不到一个装备。”因此他们加入一个保底机制,以确保一段时间不掉装备后一定会掉装备,使其按照预期的机制运行,即玩家最后总会打出传奇装备。RNG最大的黑暗秘密是——你会时常遇到这个问题,我想详细谈谈这一条——就是总的来讲,人的大脑不是很擅长处理概率问题。
在很多情况下,人脑很容易错误地理解概率,因此引入诸如保底机制之类的机制可以……嗯……玩家知道装备有百分之一的掉落概率,然后杀了二百只怪,他明白从逻辑上有可能杀的这两百只怪什么装备都没有掉落,不过他还是会很不爽地抱怨。他们没有预料到会经常出现这种情况,除非坐下好好地进行一番数学计算。而我们有关RNG的很多技巧模拟了他们的预期,使得随机性朝着玩家认为应该的那样进行,即使在数学上并不正确。保底机制正是一个例子。不过玩家仍然会经常抱怨RNG不公平,讨厌它,诅咒它……
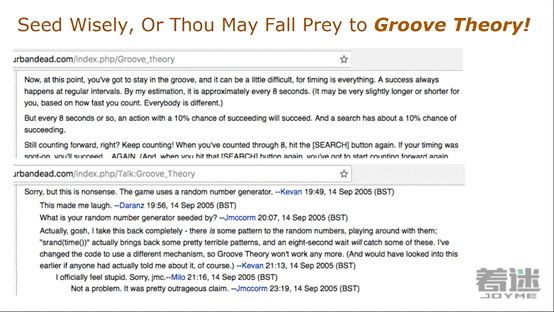
事实上我之前恰巧听到这个故事,有个叫做《Urban Dead》的游戏,一个MMO网页游戏,我很喜欢玩。游戏中包含随机点数,如果你点击攻击按钮,系统会掷点决定攻击点数。一个玩家写道:如果在沟槽中点击攻击按钮,然后进行攻击,然后在沟槽中等待八秒钟后再次攻击,他总会攻击成功。而在游戏的维基页面的顶端,这名开发者说道:“这根本不可能!我使用一个随机数字生成器了!”
如果你之前听了Squirrel的演讲,那么你应该不会被这点惊到。不过结果证明玩家是正确的。开发者只是简单地将当前时间以秒为单位输入到rand()函数中。而Squirrel的演讲提到了它最低的两位其实是不可靠的。因此每过八秒钟奇怪的事情可能就会发生。我觉得这个开发者很滑稽,首先否定了这个问题,后来才意识到这个问题。所以你不能轻易地种种子。在我们的例子中我们可能犯这个错误,所以你要透彻地思考这个问题以便你的游戏中不会出现此类bug。玩家们通常会怀疑此类按钮有bug,怀疑RNG是否出了问题。不过总会有巧合发生嘛。好了,这是游戏编程的黑暗秘密,我要把这些概念综合在一起:对于任何可能的事情,设计师总会改变他们的思路。
这对于打装备的游戏尤其适用。我的观点是,如果在设计一款打装备的游戏,或者以打装备为主的游戏时,设计师应该对其进行调整,因为这会对玩家体验以及一些你可能想不到的事情造成巨大影响,我们一会儿会提到。没错,玩家获得一件传奇装备的体验非常重要,他们要确保有保底机制,使玩家杀死boss足够多的次数后一定能得到传奇装备。
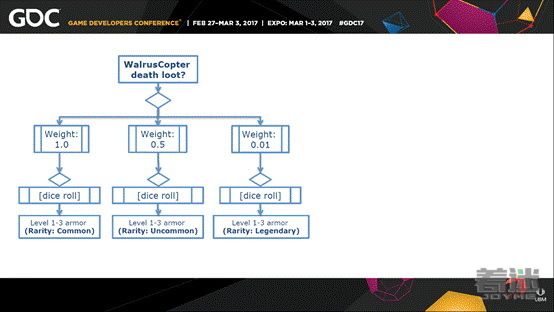
在这里我想要介绍一个工具,它能让你控制装备的掉落,详细来说这是一个查找表。没错,查找表可以表示骰子,也可以表示一副纸牌,或者其它的东西。一个加权的查找表可以这样创建:假设有52个元素,每个元素代表一张牌,每张牌的起始权重为1。如果权重可以被修改,那么这就成了一个强力的工具。你可以将一张牌的权重减为零,当它被抽走后,然后在后面再重新设置。你还可以表示很多其他内容。这里我用来表示打boss掉的装备,普通装备权重为1,罕见装备权重为0.5,罕见装备掉落的概率为普通装备的一半。
这里我实现了一个保底机制。首先这是嵌套在查找表中的查找表,有助于你响应设计者的要求,使你有很大的自由可以修改装备掉落的参数,并且加入一些细节,就像我们在这里为传奇装备加入保底机制那样。在下一张幻灯片我会介绍一些更复杂的情况。
动态加权是另一个实用的工具,在这个例子中根据保底机制传奇装备的加权会动态改变,最终会掉落。大家能看到我的鼠标吗?实际上这里我加入了回调函数,这第二个的意思是每当掉落的装备不是传奇别时,传奇装备的权重会增加。不过这仍然有悖于我的规则,即你应该考虑所有的边缘情况,从数学上讲你没有百分之百地确保传奇装备最终一定会掉落,除非同时减少其他元素的权重。这是另一种实现这个机制的方法。不过在这个例子中我只是在传奇装备没有掉出的时候简单地增加它的权重而已。当掉落后,将它的权重设置为初始值。这是一个很好的可维护的方法。
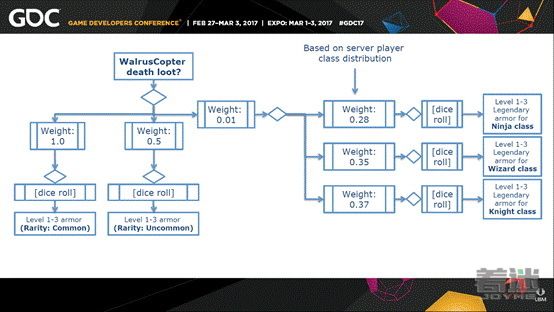
将这些串在一起:刚才我展示的一款我独立开发的游戏《Angry Henry And The Escape From The Helicopter Lords: Part 17, TheRe-Reckoning》,没错这个就是全名,为了节省我们的时间我争取不再重复它。在这个MMO游戏中,大boss是WalrusCopter,杀死他会掉装备,分为普通,罕见和传奇三个不同级别。
这是最初的实现方法,而现在我为传奇别装备加入了之前我们探讨的保底机制,使它的权重动态改变。
这里还加入了另外一层考虑,我听说很多打装备的MMO都有这个问题,即装备和游戏的经济紧密相关。我们的这个MMO游戏最初使用这个简单的实现,后来设计人员表示“我们遇到了一个问题,骑士使用的传奇装备在拍卖所的价格要比武士的传奇装备贵,我们应该改变这一点。”该如何回应这个问题呢?我推荐使用查找表的嵌套功能,为传奇装备创建子查询表,这样我们不仅有保底机制,还可以根据各职业的玩家人数设置不同职业装备的权重,这涉及到供求关系,你控制了装备的供给那么需求自然会上升。
以上是我实际遇到的一个问题。你可以通过使用如查找表之类的工具使你的代码尽量整洁且易于维护,以应对一些意想不到的问题,我推荐你使用这些工具。
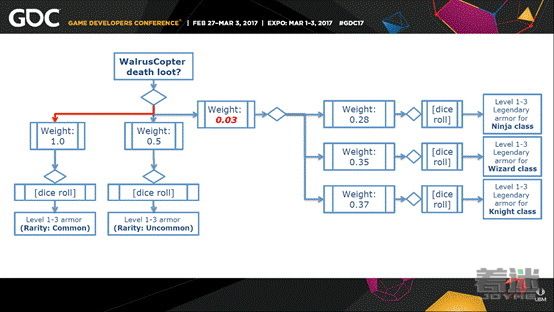
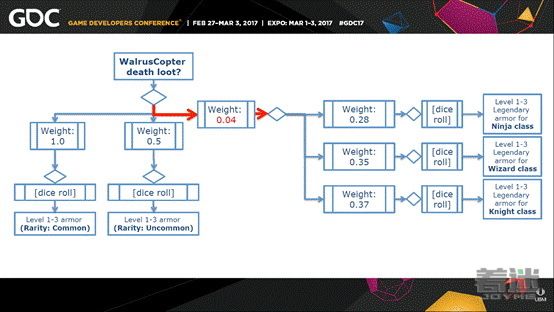
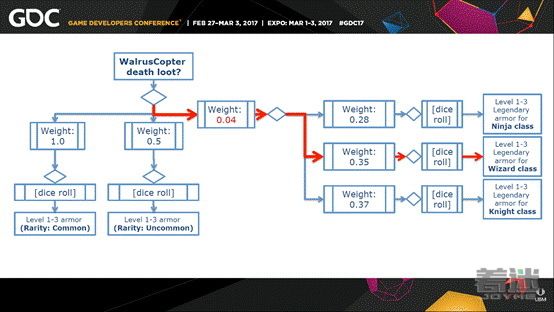
我们来看这个例子:游戏系统生成这个装备,生成这个装备,你可以看到传奇装备的权重在增加,直到最后生成传奇装备。
如果一直没有生成传奇装备那么它生成的概率会不断增加。然后会进入下一步的查找表,投出另外一个随机点数。每颗钻石代表一个随机的点数。命中后传奇装备的权重会重置。查找表是一个很有用的工具,可以用来表示任何类型的随机性,包括更简单的情况,可以用在嵌套的树形图中,使代码整洁并易于维护。
接下来,我想拓展一下Squirrel没有深入探讨的问题,即使用他的Squirrel噪音库实现一些不同的随机散列,包括随机生成一个世界。我想展示一下如何使用散列解决和RNG相关的问题,其中包含“深度重复(Deep Echoes)”问题。
我会解释它的含义。这是游戏中另一个比较奇怪的地方,有的玩家留言称他们在不同世界之间随机穿梭时,在一个世界中看到了一座和另外一个世界中相同的城市。
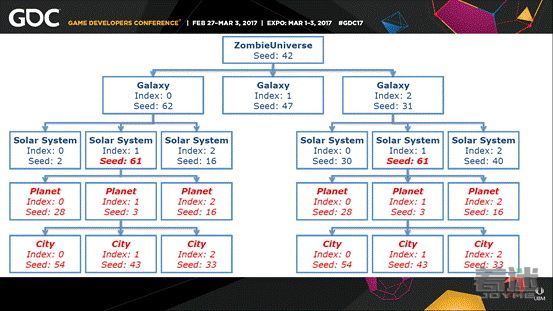
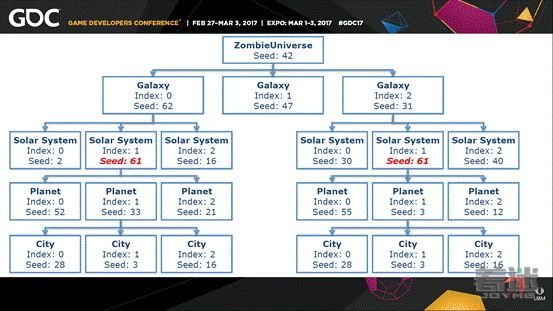
这种情况可能发生,因为通常在这种游戏中你要种种子,将种子赋给城市,然后城市会根据被赋予的种子随机生成它的构成。在这个例子中,我们有一个名为“僵尸宇宙(ZombieUniverse)”的宇宙,我们为这个顶层的宇宙设置一个种子,然后它使用该种子生成一系列的子级,即下一层的星系,然后星系又生成不同的太阳系,每个太阳系又生成不同的行星,每个星球上又有不同的城市,以及没有显示在这里的,每个城市随机生成的居民。
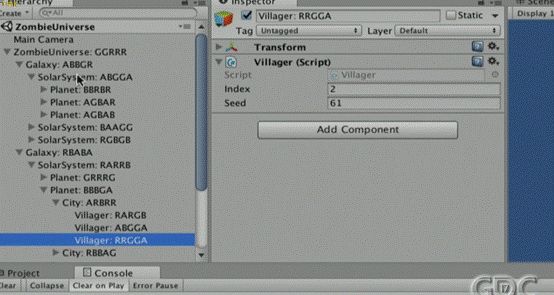
我在这里标记为红色的地方是你可能遇到的一种奇怪的情况。首先解释一下,上一层种子的作用是为了生成下一层的种子,因此顶层宇宙的种子被用来生成每个星系的种子,每个星系的种子是使用上一层的种子通过RNG得到的。那么最终我们会遇到的一个问题是有可能随机种子在不同的情况中被使用了两次,如果下面所有的内容都是使用那个种子生成的,那么你会得到完全相同的样式。在这个例子中,这两个太阳系中的所有内容都完全相同——它们所包含的行星,以及行星中的城市,甚至城市中的居民以及他们的名字、职业都是完全相同的,任何随机生成的内容现在却彼此重复,而游戏原本应该是随机的,充满噪音的,不可预测的,然而现在情况却恰恰相反。我甚至昨天晚上还在解决这个问题,最终得到了一个解决方案。这个方法有一些要注意的地方,我想要分享一下我们探索解决这个问题的过程,尤其是使用随机散列作为工具,虽然对于我们的结局方法不是最好的工具。那么,我来展示一下Unity中的一个项目来说明这个问题。希望你们都能看清楚。好了,我们稍等一下它生成,这个时间它还检查了是否有重复。在这个嵌套的结构,太阳系包含行星,行星包含城市,城市包含居民。由于这是个“僵尸宇宙”,所以居民的名字都是RARGB,ABGGA,RRGGA,看大家都在笑我还是别读了……
BRRRR!这个城市一定很冷,在北半球上吧……我们花了很长时间来解决这个问题,你会发现仍然有一些城市的种子是一样的。同样的名字或者种子。这里检查种子是否相同。现在我先不使用它。我要说明的是最终我们选择使用不同的算法来生成下面层级,而不是只依赖上一层的种子或者其它数据,这样可以避免下一层级的重复。假设我要生成一个行星,我需要生成那个行星的内容,在这个例子中即行星的名字。为了生成它的子级,我想要使用一个其它的种子,该种子是该行星独有的。在这个例子中,你可以看到种子的数值,除此之外还有个索引值(Index)。很明显,这三个子级的索引分别为0,1,2。然后我可以使用它来单独识别出这个行星。等一下……这里有两个行星的名字相同……哦,它们的种子不一样!好了,重点是你可以使用某一层级的索引沿着链条向上递归以识别该特定层。
直到24小时以前我依旧使用的是我的第一个解决方法——我对这个方法并不满意——即我们预先生成所有的种子,然后使用暴力算法确保唯一性。我并不想采用这个方法,原因之一是我们另外限制了每层可以拥有的子级的数量(即限制了最大索引数),然后只要我们生成的内容数量没有溢出,我们可以取唯一的索引数,将它们加在一起,然后乘以底数3这个最大的索引数,而不是底数2或者底数10,这样构建出一个独特的整数代表该元素的地址,这个元素递归的索引。有了这个后,我们可以将它作为一个随机数字的查找表。这个方法有些笨拙,因为我们施加了一些限制。
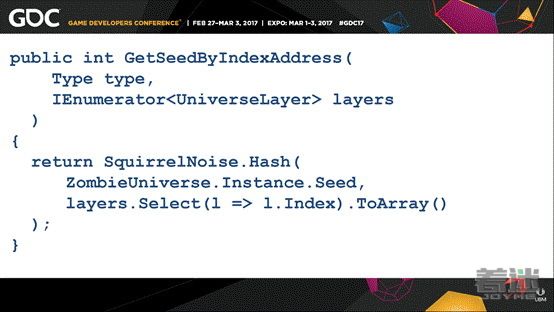
我们发现的一个更佳的方法是使用随机散列;将这个N维地址输入到一个散列函数,就是Squirrel刚才展示的那个函数。嗯……这一行可能不是那么好懂,我来解释一下:在C#中这一行的作用是把所有的层级都放入到一个数组中,然后将其输入到散列函数中。我们可以将任意数量的整数输入到该函数,并会输出一个唯一的大随机数。
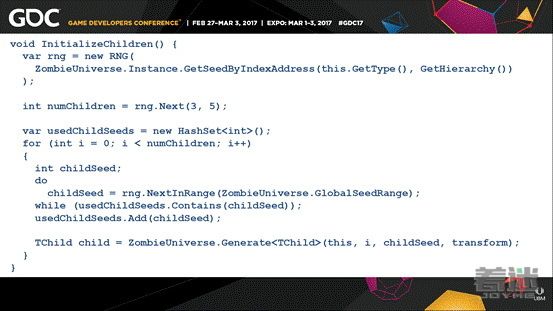
不过这个例子不保证唯一性,因此仍有重复的可能性。现在行星会基于其父级的种子生成它的内容,但是当生成子级时它使用的是对它来讲唯一的东西,这样就可以避免生成同样的子级了。这是InitializeChildren方法,该函数会生成种子。
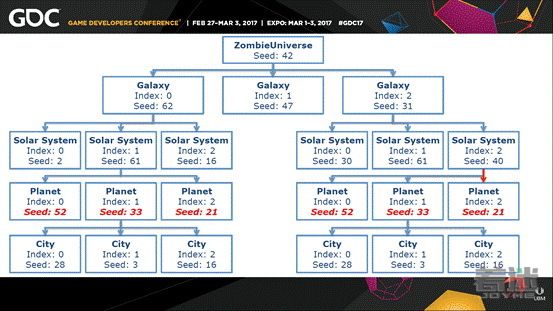
事实上,每当我要使用种子生成一个特定的元素,比如行星,居民(事实上居民不会调用该函数,因为它没有任何子级)等,我使用顶层(即宇宙)的种子。在实际使用中我发现我需要改变每一层预先生成的种子,所以如果行星拥有同样的索引那么它们的名字会相同。这个例子展示了现在的情况:现在我们可以有两个太阳系,它们的随机种子值相同,不过它们的子级不一样了,不会再发生重复情况了。
我要解释一下为什么这很重要。当然你不希望宇宙的不同部分彼此相同,不过这种重复情况的确会发生,除非你有一个完美的散列函数,当然这样的散列函数并不存在。最终在某处你一定会得到两个拥有相同种子的元素,而你不希望它们相同。这完全是为了玩家的感觉。如果他们不认为这些是随机的,那么这些就不是,比如我可以生成两座城市,它们的道路布局可能相同,但是它们的内容是完全不同的,那么玩家可能不会注意到这个使城市与众不同的表面上的元素和其它的城市是相同的,因为它们的所有上级内容都是不同的,而它们的子级内容也不同,因为我们解决这个深度重复的问题了。这一点很重要。
对了……忘记解释这个例子一个重点了,也许你已经注意到了所有种子的数值都很小,这里为了示范的效果我将种子的大小限制在0到63之间迫使这个问题出现。我这样做是为了突出这个问题,使大家明白了……首先,大家应该看到了使用这个随机散列方法时一些需要注意的地方,当我们不使用唯一的查找表后我们遇到了一个新的问题,即当我生成下一级的元素时,我使用的是一个由散列函数得到的种子,不过这里再强调一下,这个散列函数有可能产生重复的结果。现在,的确有可能两个太阳系包含同样的行星,在我的例子中它们的名称相同,在其他的例子中有可能位置相同。这看上去很糟糕,两个行星的城市完全相同,城市的名称完全相同。
对于这个“广义重复(Broad Echoes)”问题,我把它留给观众们作为一项作业,因为我的演讲超出时间了。
这个问题其实没有一个完美的答案,因为从数学上讲如果你有一个函数,输入参数的数量大于输出参数的数量,你总会遇到鸽巢问题,即如果鸽子的数量大于巢穴数量,那么最终总会有一个巢穴中有两只或以上的鸽子。当遇到这个问题时,要在编译时预先生成一个包含互不重复的种子列表,不过如果你要求输出的种子数超出限制,你仍会得到重复的种子。不过这里我们介绍了如何使用一个元素本身的独特性使得下一层生成的内容不会雷同。
看上去要到时间了,不过我还想推荐两篇我搜到的文章,它们介绍了这些工具,以及推荐了这些工具的其它使用方法。
DanCook,在他的Lost Garden博客上很好地介绍了装备表,以及它们如何嵌套,比我介绍的要有深度更详细。在Unity的博客上也有一篇博客关于使用可重复的随机数字,噪音以及散列,这篇文章令我大开眼界让我感受到了这个工具有多么的强大。你可以在上面找到更多信息。我会将这个演讲内容放在MathForGameProgrammers.com上。谢谢大家!