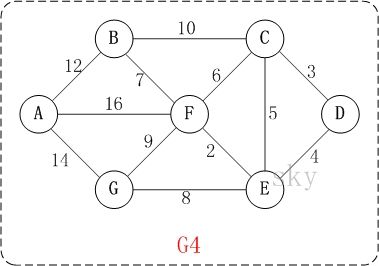
最小生成树
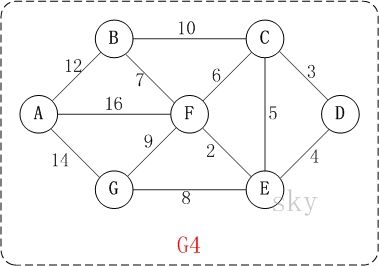
在含有n个顶点的连通图中选择n-1条边,构成一棵极小连通子图,并使该连通子图中n-1条边上权值之和达到最小,则称其为连通网的最小生成树。
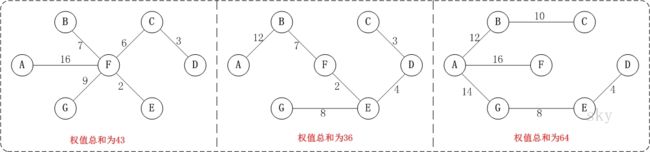
例如,对于上图中的连通网可以有多棵权值总和不相同的生成树。
Kruskal算法
1.介绍
克鲁斯卡尔(Kruskal)算法,是用来求加权连通图的最小生成树的算法。
基本思想:按照权值从小到大的顺序选择n-1条边,并保证这n-1条边不构成回路。
具体做法:首先构造一个只含n个顶点的森林,然后依照权值从小到大从连通网中选择边加入到森林中,并使得森林不产生回路,直到森林变成一棵树为止。
2.图解
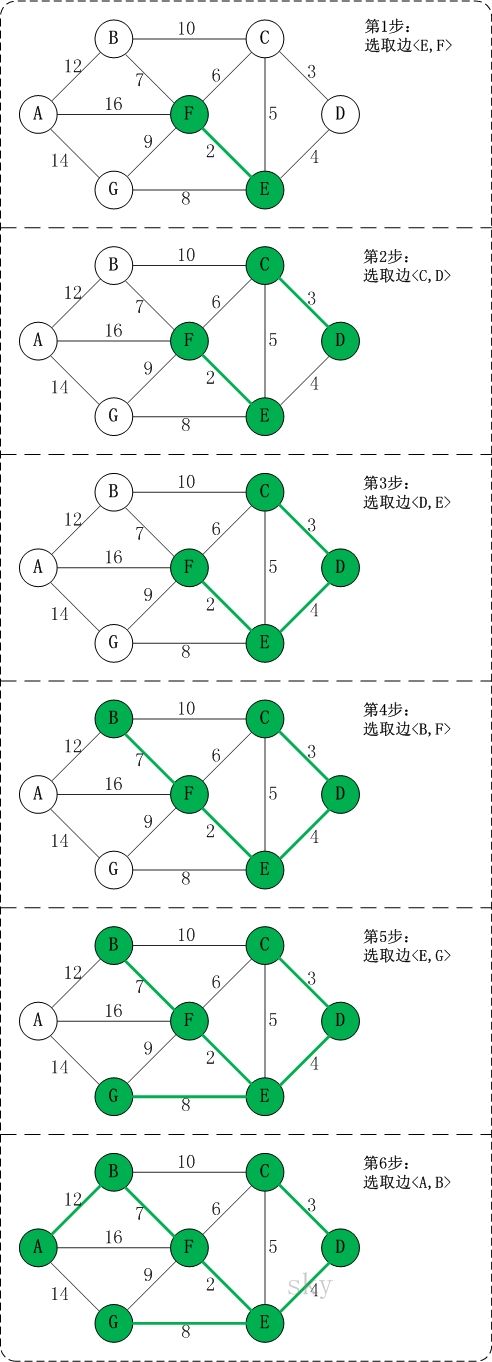
以图G4为例(更详细的可以参考《算法导论》p367),对Kruskal进行演示(假设,用数组R保存最小生成树结果)。
第1步:将边
边
第2步:将边
上一步操作之后,边
第3步:将边
上一步操作之后,边
第4步:将边
上一步操作之后,边
第5步:将边
上一步操作之后,边
第6步:将边
上一步操作之后,边
此时,最小生成树构造完成!它包括的边依次是:
3.算法分析
根据前面介绍的克鲁斯卡尔算法的基本思想和做法,我们能够了解到,克鲁斯卡尔算法重点需要解决的以下两个问题:
问题一 对图的所有边按照权值大小进行排序。
问题二 将边添加到最小生成树中时,怎么样判断是否形成了回路。
问题一用排序算法排序即可。
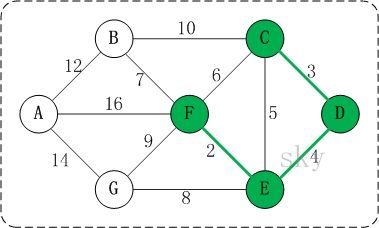
问题二,处理方式:记录顶点在“最小生成树”中的终点,顶点的终点是“在最小生成树中与它连通的最大顶点"(关于这一点,后面会通过图片给出说明)。然后每次需要将一条边添加到最小生成树时,判断该边的两个顶点的终点是否重合,重合的话则会构成回路。 以下图来进行说明:
在将
- (01) C的终点是F。
- (02) D的终点是F。
- (03) E的终点是F。
- (04) F的终点是F。
关于终点,就是将所有顶点按照从小到大的顺序排列好之后;某个顶点的终点就是"与它连通的最大顶点"。 因此,接下来,虽然
4.代码实现
package com.xushu;
/**
* Java Kruskal算法生成最小生成树(邻接表)
*/
import java.io.IOException;
import java.util.Scanner;
public class ListUDG {
private static int INF = Integer.MAX_VALUE;
// 邻接表中表对应的链表的顶点
private class ENode {
int ivex; // 该边所指向的顶点的位置
int weight; // 该边的权
ENode nextEdge; // 指向下一条弧的指针
}
// 邻接表中表的顶点
private class VNode {
char data; // 顶点信息
ENode firstEdge; // 指向第一条依附该顶点的弧
};
private int mEdgNum; // 边的数量
private VNode[] mVexs; // 顶点数组
// /*
// * 创建图(自己输入数据)
// */
// public ListUDG() {
//
// // 输入"顶点数"和"边数"
// System.out.printf("input vertex number: ");
// int vlen = readInt();
// System.out.printf("input edge number: ");
// int elen = readInt();
// if ( vlen < 1 || elen < 1 || (elen > (vlen*(vlen - 1)))) {
// System.out.printf("input error: invalid parameters!\n");
// return ;
// }
//
// // 初始化"顶点"
// mVexs = new VNode[vlen];
// for (int i = 0; i < mVexs.length; i++) {
// System.out.printf("vertex(%d): ", i);
// mVexs[i] = new VNode();
// mVexs[i].data = readChar();
// mVexs[i].firstEdge = null;
// }
//
// // 初始化"边"
// mEdgNum = elen;
// for (int i = 0; i < elen; i++) {
// // 读取边的起始顶点和结束顶点
// System.out.printf("edge(%d):", i);
// char c1 = readChar();
// char c2 = readChar();
// int weight = readInt();
//
// int p1 = getPosition(c1);
// int p2 = getPosition(c2);
// // 初始化node1
// ENode node1 = new ENode();
// node1.ivex = p2;
// node1.weight = weight;
// // 将node1链接到"p1所在链表的末尾"
// if(mVexs[p1].firstEdge == null)
// mVexs[p1].firstEdge = node1;
// else
// linkLast(mVexs[p1].firstEdge, node1);
// // 初始化node2
// ENode node2 = new ENode();
// node2.ivex = p1;
// node2.weight = weight;
// // 将node2链接到"p2所在链表的末尾"
// if(mVexs[p2].firstEdge == null)
// mVexs[p2].firstEdge = node2;
// else
// linkLast(mVexs[p2].firstEdge, node2);
// }
// }
/*
* 创建图(用已提供的矩阵)
*
* 参数说明:
* vexs -- 顶点数组
* edges -- 边
*/
public ListUDG(char[] vexs, EData[] edges) {
// 初始化"顶点数"和"边数"
int vlen = vexs.length;
int elen = edges.length;
// 初始化"顶点"
mVexs = new VNode[vlen];
for (int i = 0; i < mVexs.length; i++) {
mVexs[i] = new VNode();
mVexs[i].data = vexs[i];
mVexs[i].firstEdge = null;
}
// 初始化"边"
mEdgNum = elen;
for (int i = 0; i < elen; i++) {
// 读取边的起始顶点和结束顶点
char c1 = edges[i].start;
char c2 = edges[i].end;
int weight = edges[i].weight;
// 读取边的起始顶点和结束顶点
int p1 = getPosition(c1);
int p2 = getPosition(c2);
// 初始化node1
ENode node1 = new ENode();
node1.ivex = p2;
node1.weight = weight;
// 将node1链接到"p1所在链表的末尾"
if(mVexs[p1].firstEdge == null)
mVexs[p1].firstEdge = node1;
else
linkLast(mVexs[p1].firstEdge, node1);
// 初始化node2
ENode node2 = new ENode();
node2.ivex = p1;
node2.weight = weight;
// 将node2链接到"p2所在链表的末尾"
if(mVexs[p2].firstEdge == null)
mVexs[p2].firstEdge = node2;
else
linkLast(mVexs[p2].firstEdge, node2);
}
}
/*
* 将node节点链接到list的最后
*/
private void linkLast(ENode list, ENode node) {
ENode p = list;
while(p.nextEdge!=null)
p = p.nextEdge;
p.nextEdge = node;
}
/*
* 返回ch位置
*/
private int getPosition(char ch) {
for(int i=0; i='a'&&ch<='z') || (ch>='A'&&ch<='Z')));
return ch;
}
/*
* 读取一个输入字符
*/
private int readInt() {
Scanner scanner = new Scanner(System.in);
return scanner.nextInt();
}
/*
* 打印矩阵队列图
*/
public void print() {
System.out.printf("List Graph:\n");
for (int i = 0; i < mVexs.length; i++) {
System.out.printf("%d(%c): ", i, mVexs[i].data);
ENode node = mVexs[i].firstEdge;
while (node != null) {
System.out.printf("%d(%c) ", node.ivex, mVexs[node.ivex].data);
node = node.nextEdge;
}
System.out.printf("\n");
}
}
/*
* 获取边的权值;若start和end不是连通的,则返回无穷大。
*/
private int getWeight(int start, int end) {
if (start==end)
return 0;
ENode node = mVexs[start].firstEdge;
while (node!=null) {
if (end==node.ivex)
return node.weight;
node = node.nextEdge;
}
return INF;
}
/*
* 克鲁斯卡尔(Kruskal)最小生成树
*/
public void kruskal() {
int index = 0; // rets数组的索引
int[] vends = new int[mEdgNum]; // 用于保存"已有最小生成树"中每个顶点在该最小树中的终点。
EData[] rets = new EData[mEdgNum]; // 结果数组,保存kruskal最小生成树的边
EData[] edges; // 图对应的所有边
// 获取"图中所有的边"
edges = getEdges();
// 将边按照"权"的大小进行排序(从小到大)
sortEdges(edges, mEdgNum);
for (int i=0; i i) {
edges[index++] = new EData(mVexs[i].data, mVexs[node.ivex].data, node.weight);
}
node = node.nextEdge;
}
}
return edges;
}
/*
* 对边按照权值大小进行排序(由小到大)
*/
private void sortEdges(EData[] edges, int elen) {
for (int i=0; i edges[j].weight) {
// 交换"边i"和"边j"
EData tmp = edges[i];
edges[i] = edges[j];
edges[j] = tmp;
}
}
}
}
/*
* 获取i的终点
*/
private int getEnd(int[] vends, int i) {
while (vends[i] != 0)
i = vends[i];
return i;
}
// 边的结构体
private static class EData {
char start; // 边的起点
char end; // 边的终点
int weight; // 边的权重
public EData(char start, char end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
};
public static void main(String[] args) {
char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
EData[] edges = {
// 起点 终点 权
new EData('A', 'B', 12),
new EData('A', 'F', 16),
new EData('A', 'G', 14),
new EData('B', 'C', 10),
new EData('B', 'F', 7),
new EData('C', 'D', 3),
new EData('C', 'E', 5),
new EData('C', 'F', 6),
new EData('D', 'E', 4),
new EData('E', 'F', 2),
new EData('E', 'G', 8),
new EData('F', 'G', 9),
};
ListUDG pG;
// 自定义"图"(输入矩阵队列)
//pG = new ListUDG();
// 采用已有的"图"
pG = new ListUDG(vexs, edges);
pG.print(); // 打印图
pG.kruskal(); // Kruskal算法生成最小生成树
}
}
Prim算法
1.介绍
普里姆(Prim)算法,也是求加权连通图的最小生成树的算法。
基本思想
对于图G而言,V是所有顶点的集合;现在,设置两个新的集合U和T,其中U用于存放G的最小生成树中的顶点,T存放G的最小生成树中的边。从所有的 uЄU ,vЄ(V-U)(V-U表示除去U的所有顶点)的边中选取权值最小的边(u,v),将顶点v加入U中,将边(u,v)加入集合T中,如此不断重复,直到U=V为止,最小生成树构造完毕,此时集合T中包含了最小生成树中的所有边。
2.图解
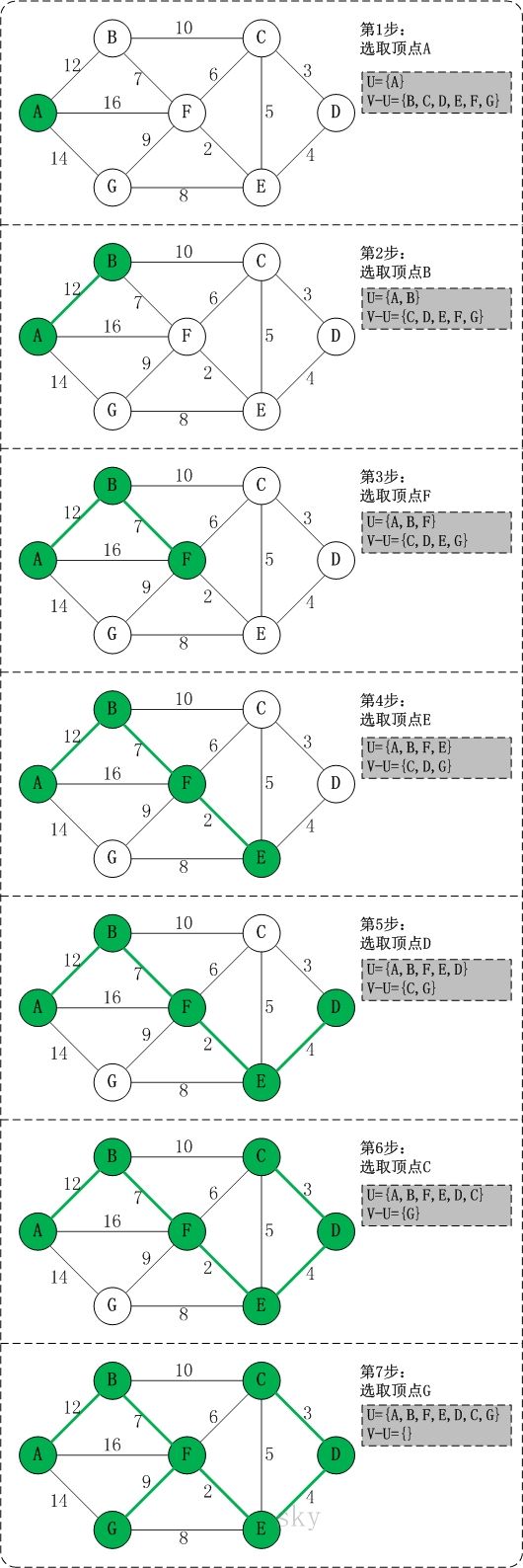
以上图G4为例,来对普里姆进行演示(从第一个顶点A开始通过普里姆算法生成最小生成树)。
初始状态:V是所有顶点的集合,即V={A,B,C,D,E,F,G};U和T都是空!
第1步:将顶点A加入到U中。
此时,U={A}。
第2步:将顶点B加入到U中。
上一步操作之后,U={A}, V-U={B,C,D,E,F,G};因此,边(A,B)的权值最小。将顶点B添加到U中;此时,U={A,B}。
第3步:将顶点F加入到U中。
上一步操作之后,U={A,B}, V-U={C,D,E,F,G};因此,边(B,F)的权值最小。将顶点F添加到U中;此时,U={A,B,F}。
第4步:将顶点E加入到U中。
上一步操作之后,U={A,B,F}, V-U={C,D,E,G};因此,边(F,E)的权值最小。将顶点E添加到U中;此时,U={A,B,F,E}。
第5步:将顶点D加入到U中。
上一步操作之后,U={A,B,F,E}, V-U={C,D,G};因此,边(E,D)的权值最小。将顶点D添加到U中;此时,U={A,B,F,E,D}。
第6步:将顶点C加入到U中。
上一步操作之后,U={A,B,F,E,D}, V-U={C,G};因此,边(D,C)的权值最小。将顶点C添加到U中;此时,U={A,B,F,E,D,C}。
第7步:将顶点G加入到U中。
上一步操作之后,U={A,B,F,E,D,C}, V-U={G};因此,边(F,G)的权值最小。将顶点G添加到U中;此时,U=V。
此时,最小生成树构造完成!它包括的顶点依次是:A B F E D C G。
4.代码实现
package com.xushu;
/**
* Java prim算法生成最小生成树(邻接表)
*/
import java.io.IOException;
import java.util.Scanner;
public class ListUDG {
private static int INF = Integer.MAX_VALUE;
// 邻接表中表对应的链表的顶点
private class ENode {
int ivex; // 该边所指向的顶点的位置
int weight; // 该边的权
ENode nextEdge; // 指向下一条弧的指针
}
// 邻接表中表的顶点
private class VNode {
char data; // 顶点信息
ENode firstEdge; // 指向第一条依附该顶点的弧
};
private VNode[] mVexs; // 顶点数组
/*
* 创建图(用已提供的矩阵)
*
* 参数说明:
* vexs -- 顶点数组
* edges -- 边
*/
public ListUDG(char[] vexs, EData[] edges) {
// 初始化"顶点数"和"边数"
int vlen = vexs.length;
int elen = edges.length;
// 初始化"顶点"
mVexs = new VNode[vlen];
for (int i = 0; i < mVexs.length; i++) {
mVexs[i] = new VNode();
mVexs[i].data = vexs[i];
mVexs[i].firstEdge = null;
}
// 初始化"边"
for (int i = 0; i < elen; i++) {
// 读取边的起始顶点和结束顶点
char c1 = edges[i].start;
char c2 = edges[i].end;
int weight = edges[i].weight;
// 读取边的起始顶点和结束顶点
int p1 = getPosition(c1);
int p2 = getPosition(c2);
// 初始化node1
ENode node1 = new ENode();
node1.ivex = p2;
node1.weight = weight;
// 将node1链接到"p1所在链表的末尾"
if(mVexs[p1].firstEdge == null)
mVexs[p1].firstEdge = node1;
else
linkLast(mVexs[p1].firstEdge, node1);
// 初始化node2
ENode node2 = new ENode();
node2.ivex = p1;
node2.weight = weight;
// 将node2链接到"p2所在链表的末尾"
if(mVexs[p2].firstEdge == null)
mVexs[p2].firstEdge = node2;
else
linkLast(mVexs[p2].firstEdge, node2);
}
}
/*
* 将node节点链接到list的最后
*/
private void linkLast(ENode list, ENode node) {
ENode p = list;
while(p.nextEdge!=null)
p = p.nextEdge;
p.nextEdge = node;
}
/*
* 返回ch位置
*/
private int getPosition(char ch) {
for(int i=0; i='a'&&ch<='z') || (ch>='A'&&ch<='Z')));
return ch;
}
/*
* 读取一个输入字符
*/
private int readInt() {
Scanner scanner = new Scanner(System.in);
return scanner.nextInt();
}
/*
* 打印矩阵队列图
*/
public void print() {
System.out.printf("List Graph:\n");
for (int i = 0; i < mVexs.length; i++) {
System.out.printf("%d(%c): ", i, mVexs[i].data);
ENode node = mVexs[i].firstEdge;
while (node != null) {
System.out.printf("%d(%c) ", node.ivex, mVexs[node.ivex].data);
node = node.nextEdge;
}
System.out.printf("\n");
}
}
/*
* 获取边的权值;若start和end不是连通的,则返回无穷大。
*/
private int getWeight(int start, int end) {
if (start==end)
return 0;
ENode node = mVexs[start].firstEdge;
while (node!=null) {
if (end==node.ivex)
return node.weight;
node = node.nextEdge;
}
return INF;
}
/*
* prim最小生成树
*
* 参数说明:
* start -- 从图中的第start个元素开始,生成最小树
*/
public void prim(int start) {
int min,i,j,k,m,n,tmp,sum;
int num = mVexs.length;
int index=0; // prim最小树的索引,即prims数组的索引
char[] prims = new char[num]; // prim最小树的结果数组
int[] weights = new int[num]; // 顶点间边的权值
// prim最小生成树中第一个数是"图中第start个顶点",因为是从start开始的。
prims[index++] = mVexs[start].data;
// 初始化"顶点的权值数组",
// 将每个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。
for (i = 0; i < num; i++ )
weights[i] = getWeight(start, i);
for (i = 0; i < num; i++) {
// 由于从start开始的,因此不需要再对第start个顶点进行处理。
if(start == i)
continue;
j = 0;
k = 0;
min = INF;
// 在未被加入到最小生成树的顶点中,找出权值最小的顶点。
while (j < num) {
// 若weights[j]=0,意味着"第j个节点已经被排序过"(或者说已经加入了最小生成树中)。
if (weights[j] != 0 && weights[j] < min) {
min = weights[j];
k = j;
}
j++;
}
// 经过上面的处理后,在未被加入到最小生成树的顶点中,权值最小的顶点是第k个顶点。
// 将第k个顶点加入到最小生成树的结果数组中
prims[index++] = mVexs[k].data;
// 将"第k个顶点的权值"标记为0,意味着第k个顶点已经排序过了(或者说已经加入了最小树结果中)。
weights[k] = 0;
// 当第k个顶点被加入到最小生成树的结果数组中之后,更新其它顶点的权值。
for (j = 0 ; j < num; j++) {
// 获取第k个顶点到第j个顶点的权值
tmp = getWeight(k, j);
// 当第j个节点没有被处理,并且需要更新时才被更新。
if (weights[j] != 0 && tmp < weights[j])
weights[j] = tmp;
}
}
// 计算最小生成树的权值
sum = 0;
for (i = 1; i < index; i++) {
min = INF;
// 获取prims[i]在矩阵表中的位置
n = getPosition(prims[i]);
// 在vexs[0...i]中,找出到j的权值最小的顶点。
for (j = 0; j < i; j++) {
m = getPosition(prims[j]);
tmp = getWeight(m, n);
if (tmp < min)
min = tmp;
}
sum += min;
}
// 打印最小生成树
System.out.printf("PRIM(%c)=%d: ", mVexs[start].data, sum);
for (i = 0; i < index; i++)
System.out.printf("%c ", prims[i]);
System.out.printf("\n");
}
// 示例类:边的结构体(用来演示)
private static class EData {
char start; // 边的起点
char end; // 边的终点
int weight; // 边的权重
public EData(char start, char end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
};
public static void main(String[] args) {
char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
EData[] edges = {
// 起点 终点 权
new EData('A', 'B', 12),
new EData('A', 'F', 16),
new EData('A', 'G', 14),
new EData('B', 'C', 10),
new EData('B', 'F', 7),
new EData('C', 'D', 3),
new EData('C', 'E', 5),
new EData('C', 'F', 6),
new EData('D', 'E', 4),
new EData('E', 'F', 2),
new EData('E', 'G', 8),
new EData('F', 'G', 9),
};
ListUDG pG;
// 自定义"图"(输入矩阵队列)
//pG = new ListUDG();
// 采用已有的"图"
pG = new ListUDG(vexs, edges);
//pG.print(); // 打印图
//pG.DFS(); // 深度优先遍历
//pG.BFS(); // 广度优先遍历
pG.prim(0); // prim算法生成最小生成树
}
}