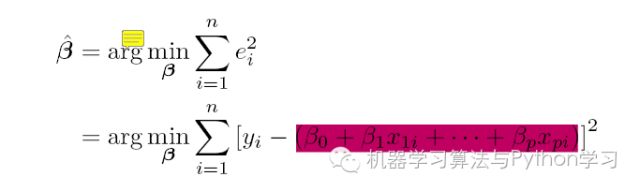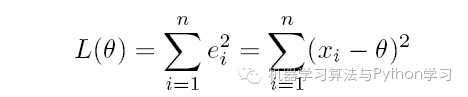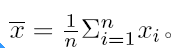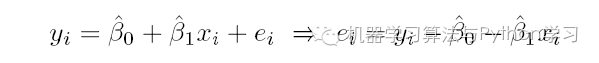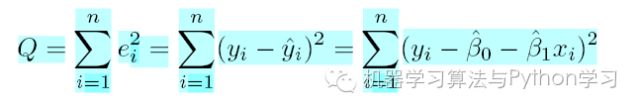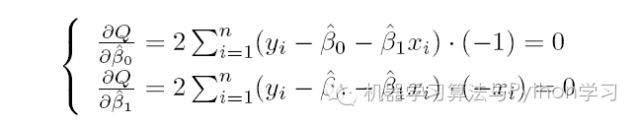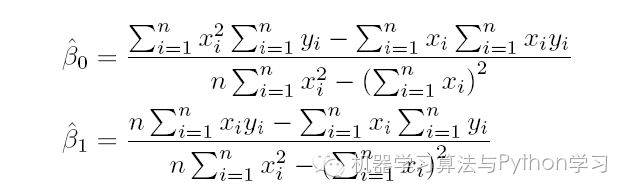上次了解了核函数与损失函数之后,支持向量机的理论已经基本完成,今天将谈论一种数学优化技术------最小二乘法(Least Squares, LS)。现在引用一下《正态分布的前世今生》里的内容稍微简单阐述下。我们口头中经常说:一般来说,平均来说。如平均来说,不吸烟的健康优于吸烟者,之所以要加“平均”二字,是因为凡事皆有例外,总存在某个特别的人他吸烟但由于经常锻炼所以他的健康状况可能会优于他身边不吸烟的朋友。而最小二乘法的一个最简单的例子便是算术平均。
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。用函数表示为:
使误差平方和达到最小以寻求估计值的方法,就叫做最小二乘法,用最小二乘法得到的估计,叫做最小二乘估计。当然,取平方和作为目标函数只是众多可取的方法之一。
最小二乘法是Legendre 在1806 年发表的,基本思想就是认为测量中有误差,我们求解出导致累积误差最小的参数即可。
对最小二乘法的优良性做了几点说明:
最小二乘使得误差平方和最小,并在各个方程的误差之间建立了一种平衡,从而防止某一个极端误差取得支配地位
计算中只要求偏导后求解线性方程组,计算过程明确便捷
最小二乘可以导出算术平均值作为估计值
对于最后一点,从统计学的角度来看是很重要的一个性质。推理如下:假设真值为θ,x1, x2, · · · , xn 为n 次测量值,每次测量的误差为ei = xi − θ,按最小二乘法,误差累积为:
求解θ 使L(θ) 达到最小,正好是算术平均
由于算术平均是一个历经考验的方法,而以上的推理说明,算术平均是最小二乘的一个特例,所以从另一个角度说明了最小二乘方法的优良性,使我们对最小二乘法更加有信心。
最小二乘法发表之后很快得到了大家的认可接受,并迅速的在数据分析实践中被广泛使用。不过历史上又有人把最小二乘法的发明归功于Gauss,这又是怎么一回事呢。Gauss 在1809 年也发表了最小二乘法,并且声称自己已经使用这个方法多年。Gauss 发明了小行星定位的数学方法,并在数据分析中使用最小二乘方法进行计算,准确的预测了谷神星的位置。
说了这么多,貌似跟本文的主题支持向量机没啥关系呀,别急,请让我继续阐述。本质上说,最小二乘法即是一种参数估计方法,说到参数估计,咱们得从一元线性模型说起。
什么是一元线性模型呢?先来梳理下几个基本概念:
(1) 监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。
(2) 回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。
(3) 如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
(4) 对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面。
对于一元线性回归模型, 假设从总体中获取了n 组观察值(x1, y1), (x2, y2), · · · , (xn, yn)。对于平面中的这n个点,可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看,这条直线处于样本数据的中心位置最合理。
选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。有以下三个标准可以选择:
1. 用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
2. 用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
3. 最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外,得到的估计量还具有优良特性。这种方法对异常值非常敏感。
最常用的是普通最小二乘法Ordinary Least Square, OLS :所选择的回归模型应该使所有观察值的残差平方和达到最小,即采用平方损失函数。
我们定义样本回归模型为:
其中ei 为样本(xi, yi) 的误差。定义平方损失函数:
SMO 算法则通过Q 最小确定这条直线,即确定β0 和 β1,以β0 和 β1 为变量,把它们看作是Q 的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q 对两个待估参数的偏导数并令其等于0:
求解可以得到:
这就是最小二乘法的解法,就是求得平方损失函数的极值点。自此,你看到求解最小二乘法与求解SVM 问题何等相似,尤其是定义损失函数,而后通过偏导求得极值。
上面仅仅给出了SMO算法的最终求解公式,并未给出具体的求解过程,这个内容将在明天给出,也是关于支持向量机基本理论的最后一点内容~~~~