由于最近初学,故写下此笔记
我们在讲解隐马模型之前,先了解一下马尔科夫模型:
每个状态只依赖之前有限个状态:
N阶马尔科夫:依赖之前n个状态
1阶马尔科夫:仅仅依赖之前一个状态
马尔科夫模型重要的三类参数:
状态
初始概率
状态转移概率
那么其中状态状态转移概率怎么计算得到:
p(St+1=l|St=k)=l紧跟k出现的次数/k出现的总次数,我们可以这样理解:转移概率由一个状态到另外一个状态的转移概率,前一个字和后面一个字的词性相同过的概率还是比较大的, 根据贝叶斯公式
p(A,B)= p(B|A)*p(A)计算出各个状态转移的概率
初始概率是怎么计算得到:P(S1=k)=k 作为序列开始的次数/观测序列总数 也可以这么理解:查看该状态的开头有多少个字,计算一下该状态的概率
马尔科夫模型是对一个序列数据的建模,但是有时候我们会对两个序列数据进行建模,因此就引出了隐马尔科夫模型即HMM
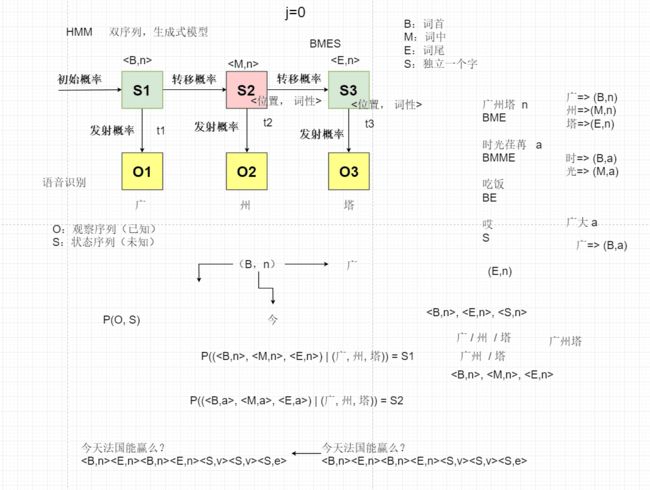
例如:我们在发音真高兴的时候,语音为zhen,gao,xing三个观察序列,观察序列为已知的,期望找到真高兴三个状态序列,或是下面图中的广州塔,首先对每个观测序列进行分析背后的状态和词性(B代表开始,M代表中间,E代表结束,S代表单个词,但是这个状态只是针对词语,对于句子还需要另外区分其状态)。
发射概率意思是在“真”词中,发射出zhen的语音概率为多大
那么什么是隐马:
每一个时刻的状态都是不可见的, 没法观测到一个s1, s2, ..., st的 状态, 但是HMM在每个时刻都会输出一个符号ot, 而且ot仅与st相关, 这个称为独立输出假设。 So, HMM是基于马尔科夫假设和独立输出假设。
我们由此可以计算出, 在某个特定的状态序列s1 , s2, .., st 产生o1, o2, ..., ot的概率: 根据乘法公式展开:
P(s1 , s2, .., st , o1, o2, ..., ot) = P(o1, o2, ..., ot | s1 , s2, .., st) * P(s1 , s2, .., st) = P(ot | st) * P(st | st-1) , t从1 到 T 连乘, 其中在语音识别中P(s1 , s2, .., st) 称为语言模型, P(o1, o2, ..., ot | s1 , s2, .., st) 称为声学模型。
到此为止基本的概念就介绍完了, 不难发现,HMM 其实只是一种结构模型,由一系列的参数来构成 入 = (PI, A , B),其中PI 是初始的状态概率, A是状态之间的转移概率矩阵, B是在某一状态下到观测值之间的生成概率矩阵
那么有了隐马,这个隐马主要是来解决什么问题,因此抛出隐马解决的三个问题:
1、 给定一个模型,如何计算出某个特定的输出序列的概率
2、 给定一个模型和某个特定的输出序列,如何找到最可能产生这个输出的状态序列
3、 给定足够的观测数据, 如何估计出HMM的参数(即转移概率矩阵和省城概率矩阵)
这里为只说明一下每个问题的解决的方式,由于知识有限,
第一个问题,我们需要采用前向后向算法来解决该问题,那么什么是前向算法和后向算法:
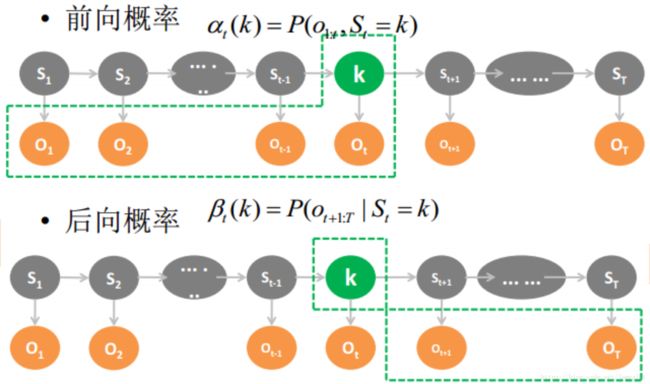
前向概率解决问题;当一个状态为K的前提下,计算t时刻为k的观测序列的概率
后向概率解决问题:当t时刻状态为k的前提下,计算t+1时刻到T时刻观测序列的概率。
第二个问题,这里我们就需要引出Viterbi算法,利用动态规划求最优的路径的方式来求解,那么什么是Viterbi算法
维特比算法是一个特殊但应用最广的动态规划算法,它是针对篱笆网络的有向图(Lattice)的最短路径问题而提出的。凡是使用隐含马尔可夫模型描述的问题都可以用维特比算法来解码,包括今天的数字通信、语音识别、机器翻译、拼音转汉字、分词等,通俗的讲就是利用HMM模型来达到计算最优路径的算法,既然要利用HMM模型,那么就离不开HMM的五大参数来求解
状态
观测序列
初始概率
状态转移概率
发射概率
我们用一个例子来解释这个Viterbi算法:
一、背景
假如我的身体情况只有两种可能:健康或者发烧。
假设没有体温计或者百度这种神奇东西,我唯一判断他身体情况的途径就是到楼下的猪大炮询问。
猪大炮通过询问我的感觉,判断我的病情,再假设我只会回答正常、头晕或冷。
第一天我告诉猪大炮感觉正常。
第二天我告诉猪大炮感觉有点冷。
第三天我告诉猪大炮感觉有点头晕。
那么问题来了,猪大炮如何根据我的描述的情况,推断出这三天中我的一个身体状态呢?
二、已知情况
隐含的身体状态 = { 健康 , 发烧 }
可观察的感觉状态 = { 正常 , 冷 , 头晕 }
猪大炮预判的我身体状态的概率分布 = { 健康:0.6 , 发烧: 0.4 }
猪大炮认为的我身体健康状态的转换概率分布 = {
健康->健康: 0.7 ,
健康->发烧: 0.3 ,
发烧->健康:0.4 ,
发烧->发烧: 0.6
}
猪大炮认为的在相应健康状况条件下,我的感觉的概率分布 = {
健康,正常:0.5 ,冷 :0.4 ,头晕: 0.1 ;
发烧,正常:0.1 ,冷 :0.3 ,头晕: 0.6
}
我连续三天的身体感觉依次是: 正常、冷、头晕 。
三、题目:
已知如上,求:我这三天的身体健康状态变化的过程是怎么样的?
四、求解过程
根据 Viterbi 理论,后一天的状态会依赖前一天的状态和当前的可观察的状态。那么只要根据第一天的正常状态依次推算找出到达第三天头晕状态的最大的概率,就可以知道这三天的身体变化情况。
传不了图片,悲剧了。。。
1.初始情况:
P(健康) = 0.6,P(发烧)=0.4。
2.求第一天的身体情况:
计算在我感觉正常的情况下最可能的身体状态。
P(今天健康) = P(健康|正常)*P(健康|初始情况) = 0.5 * 0.6 = 0.3
P(今天发烧) = P(发烧|正常)*P(发烧|初始情况) = 0.1 * 0.4 = 0.04
那么取最优就可以认为第一天最可能的身体状态是:健康。
3.求第二天的身体状况:
计算在我感觉冷的情况下最可能的身体状态。
那么第二天有四种情况,由于第一天的发烧或者健康转换到第二天的发烧或者健康。
P(前一天发烧,今天发烧) = P(发烧|前一天)*P(发烧->发烧)*P(冷|发烧) = 0.04 * 0.6 * 0.3 = 0.0072
P(前一天发烧,今天健康) = P(健康|前一天)*P(发烧->健康)*P(冷|健康) = 0.04 * 0.4 * 0.4 = 0.0064
P(前一天健康,今天健康) = P(发烧|前一天)*P(健康->健康)*P(冷|健康) = 0.3 * 0.7 * 0.4 = 0.084
P(前一天健康,今天发烧) = P(健康|前一天)*P(健康->发烧)*P(冷|发烧) = 0.3 * 0.3 *.03 = 0.027
那么取最优可以认为,第二天最可能的状态是:健康。
4.求第三天的身体状态:
计算在我感觉头晕的情况下最可能的身体状态。
P(前一天发烧,今天发烧) = P(发烧|前一天)*P(发烧->发烧)*P(头晕|发烧) = 0.027 * 0.6 * 0.6 = 0.00972
P(前一天发烧,今天健康) = P(健康|前一天)*P(发烧->健康)*P(头晕|健康) = 0.027 * 0.4 * 0.1 = 0.00108
P(前一天健康,今天健康) = P(发烧|前一天)*P(健康->健康)*P(头晕|健康) = 0.084 * 0.7 * 0.1 = 0.00588
P(前一天健康,今天发烧) = P(健康|前一天)*P(健康->发烧)*P(头晕|发烧) = 0.084 * 0.3 *0.6 = 0.01512
那么取最优可以认为:第三天最可能的状态是发烧。
五、结论:
根据如上计算。这样猪大炮断定,我这三天身体变化的序列是:健康->健康->发烧。
这个算法大概就是通过已知的可以观察到的序列,和一些已知的状态转换之间的概率情况,通过综合状态之间的转移概率和前一个状态的情况计算出概率最大的状态转换路径,从而推断出隐含状态的序列的情况。