方差分析用于两个及两个以上样本均值差别的显著性检验,方差分析分为单因素方差分析和多因素方差分析。在进行方差分析时,对数据有一定要求:独立、正态、方差齐次(各水平间)。
单因素方差分析#
小白鼠在接种了3种不同菌型的伤寒杆菌后的存活天数如表所示,判断小白鼠被注射三种菌型后的平均存活天数有无显著差异。
| 存活时间 | 药物类型 | 存活时间 | 药物类型 | 存活时间 | 药物类型 |
|---|---|---|---|---|---|
| 2 | 1 | 5 | 2 | 7 | 3 |
| 4 | 1 | 6 | 2 | 11 | 3 |
| 3 | 1 | 8 | 2 | 6 | 3 |
| 2 | 1 | 5 | 2 | 6 | 3 |
| 4 | 1 | 10 | 2 | 7 | 3 |
| 7 | 1 | 7 | 2 | 9 | 3 |
| 7 | 1 | 12 | 2 | 5 | 3 |
| 2 | 1 | 12 | 2 | 5 | 3 |
| 2 | 1 | 6 | 2 | 10 | 3 |
| 5 | 1 | 6 | 2 | 6 | 3 |
| 4 | 1 | 3 | 3 | ||
| 10 | 3 |
mouse <- data.frame(X=c( 2, 4, 3, 2, 4, 7, 7, 2, 2, 5, 4, 5, 6, 8, 5, 10, 7,
12, 12, 6, 6, 7, 11, 6, 6, 7, 9, 5, 5, 10, 6, 3, 10),
A=factor(c(rep(1,11),rep(2,10), rep(3,12))))
mouse.aov <- aov(X ~ A, data=mouse)
summary(mouse.aov)
Df Sum Sq Mean Sq F value Pr(>F)
A 2 94.26 47.13 8.484 0.0012 **
Residuals 30 166.65 5.56
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
从上面的结果上看p值0.0012小于0.05说明不同药物对小白鼠存活天数有显著影响。
多因素方差分析#
使用4种燃料,3种类型的推进器做火箭射程试验,每一种组合情况做一次试验,分析各种燃料A与各种推进器B对火箭射程有无显著影响?
| 实验数据 | A1 | A2 | A3 | A4 |
|---|---|---|---|---|
| B1 | 582 | 491 | 601 | 758 |
| B2 | 562 | 541 | 709 | 582 |
| B3 | 653 | 516 | 392 | 487 |
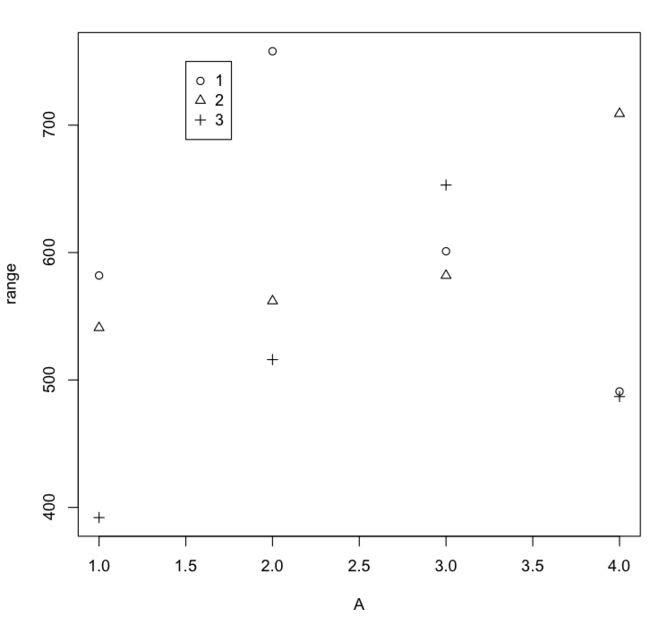
首先通过重叠散点图观察一下数据,看起来不同燃料下不同推进器对射程没有明显影响。
range=c(582,562,653,491,541,516,601,709,392,758,582,487)
A=rep(c(1,2,3,4), 3)
B=rep(c(1,2,3), 4)
plot(range ~ A, pch=B)
legend(1.5, 750, legend=1:3, pch=B)
接下来我们做多因素方差分析
A = factor(A)
B = factor(B)
range.aov <- aov(range ~ A + B)
range.aov
Call:
aov(formula = range ~ A + B)
Terms:
A B Residuals
Sum of Squares 23339.00 22384.67 65618.00
Deg. of Freedom 3 2 6
Residual standard error: 104.5769
Estimated effects may be unbalanced
summary(range.aov)
Df Sum Sq Mean Sq F value Pr(>F)
A 3 23339 7780 0.711 0.580
B 2 22385 11192 1.023 0.415
Residuals 6 65618 10936
我们看到P值均大于0.05,假设检验没有通过,说明4种燃料和3种类型的推助器对火箭射程并无显著影响。