“Able was I ere I saw Elba.” - Napoleon Bonaparte
“在我看到厄尔巴岛之前,我曾无所不能。”——拿破仑·波拿巴
圣伯纳山口的陡坡上,天色阴沉。一条小道蜿蜒伸向山顶的隘口,士兵们正推拉着辎重,在巨石间艰难地向山顶前进。在山间的一块小平地上,一匹战马双蹄跃起,年轻的法国第一执政官身披红色斗篷,左手拉住缰绳,右手指向高高的山峰,目光镇定而坚毅,充满着梦想和自信。
这就是法国画家雅克-路易·大卫著名的画作《跨越阿尔卑斯山圣伯纳隘道的拿破仑》,画作上的拿破仑正带领着军队跨越阿尔卑斯山,前往意大利解救被围困在热那亚的法军。
大卫是拿破仑的御用画师,他笔下的拿破仑一直是威武、高大的形象。在这幅画的左下角,我们还可以看到三块石头,上面分别刻有“BONAPARTE”,“HANNIBAL”和“KAROLUS MAGNUS”的字样。这三个人的名字,头一个是拿破仑,后两个分别是汉尼拔和查理大帝。大卫把拿破仑奔袭意大利和历史上迦太基统帅汉尼拔击败罗马人以及查理大帝征战意大利的战绩相媲美,其忠心表露无疑。
有人说:历史是个任人打扮的小姑娘。在画家的笔下,历史是最容易被ps和美颜的。很多历史学家指出,拿破仑当年跨越阿尔卑斯山时远没有画面上这么精神。首先,抄近道翻山越岭进入意大利,目的就是要给对手来个出其不意,作为军事奇才的拿破仑不可能穿着这么一件颜色鲜艳的斗篷摆pose,生怕对方探马看不到他;其次,战马在平地上有很强的战斗力和冲击力,但在陡峭蜿蜒的山路上,战马远远没有毛驴或着骡子实用;第三,拿破仑奔袭意大利,目的是解救被围的法军,当时的心情一定是紧张和焦虑的,很难做到画面上这么淡定自如。
这么分析下来,历史学家的观点是相对合理的,更何况他们还找到了另一位画家同样题材的画作,和大卫的大作相比,保罗·德拉罗什这幅《拿破仑越过阿尔卑斯山》才更像当时场景的真实写照。画面中,骑在毛驴上的拿破仑穿着一件普通的灰绿色军大衣,因为肠胃不好,他的右手插入大衣捂着肚子,神情疲惫;旁边的扈从左手拿着探路长棍,右手牵着毛驴,正艰难地在积雪覆盖的山路上前行。
当然,抄近道进入意大利的拿破仑最终在马伦哥战役中击败奥地利军队,决定了意大利战场的胜利。胜利者有权在画家笔下骑上白马、穿上红色斗篷、意气风发;胜利者同样有权在数学史上留下他的名字,这就是所谓的“拿破仑三角形”。
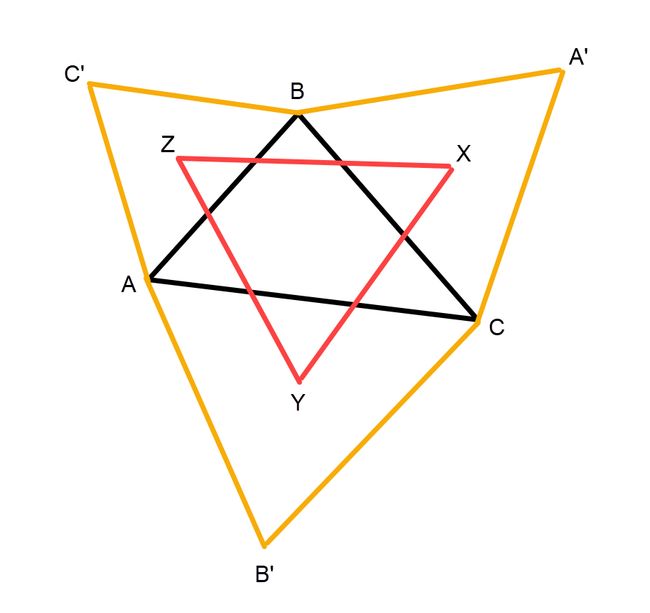
拿破仑三角形,是指对于任意三角形ABC而言,从三条边分别向外做等边三角形,则三个等边三角形的三个中心XYZ将形成一个新的等边三角形。
等边三角形XYZ被称之为拿破仑三角形,传说中拿破仑最先发现了三角形的这一特性。历史上的拿破仑读过炮兵学院,他的数学成绩确实很好;但要说他最先发现了拿破仑三角形,这很可能不是事实,恐怕也是所谓“美颜”的结果。
美国的数学教育家Alfred S. Posamentier在《三角形的奥秘:一段数学旅程》中指出,拿破仑三角形的这个特性出现在出版物中,最早是在1825年英国数学家William Rutherford的一本名为The ladies diary的书中,而当时拿破仑已经死去4年了;所以,甚至拿破仑是否知道三角形的这一特性目前来看都是存疑的。
我们先撇开拿破仑,来看看如何证明拿破仑三角形的这个特性。
既然是三角形,首先当然应该尝试纯几何的方法。
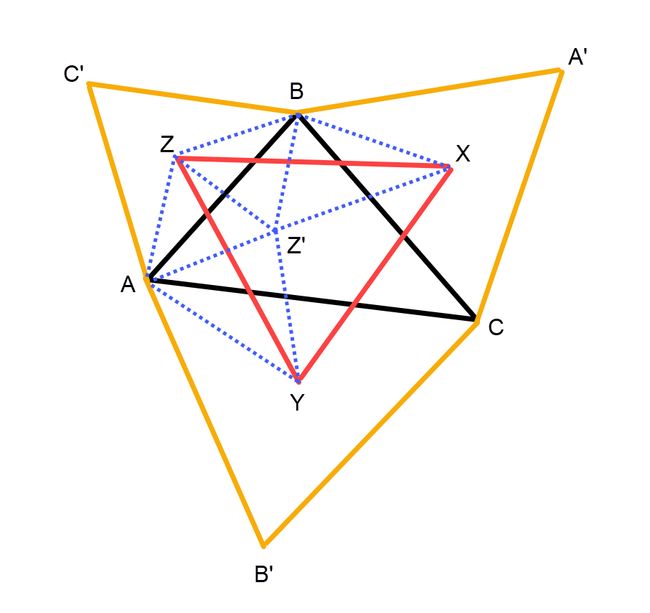
设点Z’是点Z关于边AB的对称点,连接ZZ’,ZA,ZB,XB,YA,Z’A,Z’B,Z’X和Z’Y。
因为Z是等边三角形ABC’的中心,Z’和Z关于AB对称,容易知道
∠ZAB = ∠Z’AB = ∠ZBA = ∠Z’BA = 30°,且|ZA| = |ZB| = |Z’A| = |Z’B|
所以,三角形AZZ’和三角形BZZ’是两个全等的等边三角形。
又因为,∠Z’AB = ∠YAC = 30°,所以∠BAC = ∠Z’AC + 30° = ∠Z’AY。
同时,|Z’A| = |BA| / √ 3,|YA| = |CA| / √ 3
所以,三角形Z’AY相似于三角形BAC;同理,三角形BZ’X相似于三角形BAC;又因为|Z’A| = |BZ’|,所以三角形Z’AY与三角形BZ’X全等。
因此∠Z’AY = ∠BZ’X,|YA| = |XZ’|。
考虑三角形ZAY和三角形ZZ’X,因为|ZA| = |ZZ’|,|YA| = |XZ’|,
又因为∠ZAY = ∠Z’AY + 60° = ∠BZ’X + 60° = ∠ZZ'X
所以三角形ZAY和三角形ZZ’X全等,因此ZY = ZX。
同理可得ZX = XY,三角形XYZ为等边三角形,得证。
这个解法虽然只用到了纯粹的几何知识,但作出了多条辅助线,需要证明两对三角形全等,稍微显得有些复杂。下面我们来看看使用三角函数的方法,虽然需要用到三角函数的和差公式,但解题思路相对简单。
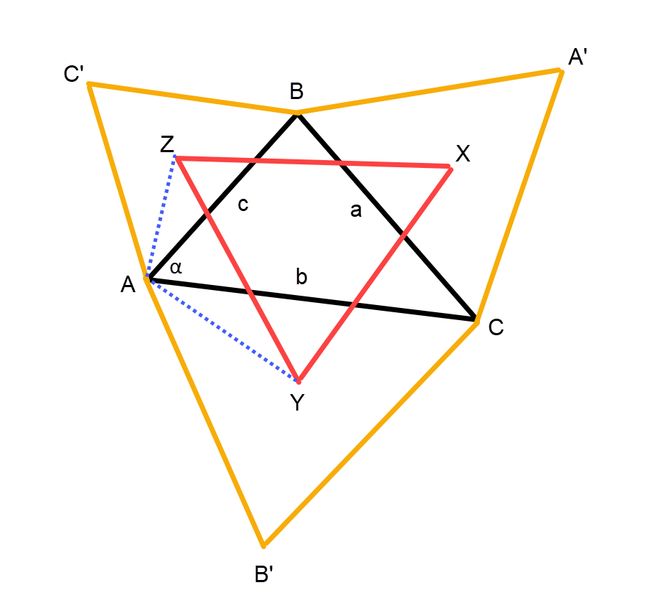
设三角形ABC的三条边长度分别为a,b和c,∠BAC为α。连接ZA和YA,易知∠ZAB = ∠YAC = 30°。
考虑三角形ZAY,根据余弦定理,
|ZY|2 = |ZA|2 + |YA|2 - 2|ZA|·|YA|·Cos(α + 60°)
= 1/3·c2 + 1/3·b2 - 2/3·bc·(1/2·Cosα - √3/2·Sinα)
= 1/3·c2 + 1/3·b2 - 1/3·bc·Cosα + √3/3·bc·Sinα (式1)
考虑三角形BAC,
根据余弦定理,bc·Cosα = 1/2·(c2 + b2 - a2) (式2)
根据正弦面积公式,bc·Sinα = 2·SABC (式3)
将式2,式3代入式1,得到|ZY|2 = 1/3·c2 + 1/3·b2 - 1/6·(c2 + b2 - a2) + 2√3/3·SABC
即,|ZY|2 = 1/6·(a2 + b2 + c2) + 2√3/3·SABC
上式关于a,b和c对称,所以|ZY|2 = |YX|2 = |XZ|2,即三角形XYZ为等边三角形,得证。
我们知道,几何平面中的一个点也可以表示成为复平面上的一个点,或者一个复数,几何平面中的边等同于复平面上的一个无向向量。复平面上向量的旋转、拉伸、连接等操作可以通过复数的计算来表示,许多平面几何的问题,都可以通过复数运算得到比较简洁的解答。拿破仑三角形同样也可以通过复平面的计算得以证明,有兴趣的朋友可以在这方面继续深入了解。
除了向外作等边三角形,在三条边上分别向内作等边三角形可以得到另一个较小的拿破仑三角形。
其证明方式类似于向外作三角形得到的拿破仑三角形。对于几何解法来说,同样可以将点Z对边AB向外作对称操作得到点Z’,然后通过两对三角形的全等进行证明。三角函数证明更加直观一些,只不过向外作出的∠ZAY等于α + 60°,而向内作出的∠ZAY等于α - 60°或者60° - α,整个证明过程几乎完全相同,只不过式子中正弦函数项以及后续的三角形面积项的符号相反,式子仍然具有对称性。有兴趣的朋友可以自行证明。
拿破仑三角形还有一些有趣的性质。比如,
1)线段AA’,BB’和CC’长度相等,互相之间夹角为120度,且三线共点F。
2)线段AA’垂直于线段YZ,BB’垂直于ZX,CC’垂直于XY。
3)三个等边三角形ABC’,BCA’和CAB’的外接圆相交于一点,该点即线段AA’,BB’和CC’的交点F。
这些性质中,最有意思的就是这个点F了。为啥叫它F,因为它和费马有关。
皮埃尔·德·费马是数学史上的一个奇人,他出生在十七世纪的法国,本职工作是一名律师。想必在那个年代律师就已经是一个很赚钱的职业了,所以费马有很多空闲时间可以用于他的业余爱好——数学研究之中。费马的这种爱好和现在的“民间科学家”的癖好有着天壤之别,虽然人们称他为“业余数学家”,实际上他的数学水平以及对数学的贡献丝毫不亚于那个年代任何一个知名的数学家,费马在数论、解析几何和概率论上都很有成就,著名的费马大定理、费马小定理即以他的名字命名。
某一天,费马给伽利略的学生、意大利物理学家托里切利写了一封信,信中提出了这样一个问题:在已知三角形的内部找到一个点,使得这个点到三角形三个顶点的距离之和为最小。这样的一个点后来被人们称之为费马点。
很容易发现,这个问题不仅仅是个纯数学问题,而且还有很强的实际应用价值。比如在三个村庄的中间建一个集市,要使得三个村庄与集市之间的距离之和最短。如果我们把三个点扩大到若干个点,对费马点的寻找就转化成为现代物流中的最优选址问题。
下面我们来解决寻找费马点的问题。
如果只有两个点,问题很简单,两点间线段最短,所以这两个点之间线段上的每一个点都是费马点。现在扩大到不共线的三个点(即三角形的三个顶点),还能使用两点间线段最短的法则吗?答案是可以,但需要一点点技巧。
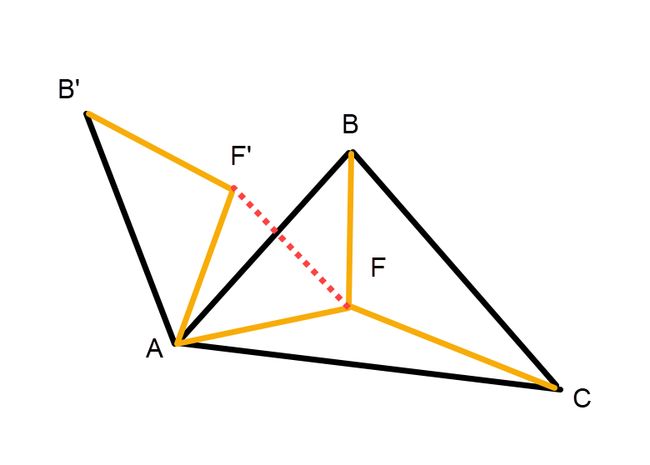
对于三角形ABC内的一个点F,我们先将AF,BF和CF连接起来。我们将三角形ABF,以A为旋转中心,逆时针旋转60度到三角形AB’F’的位置。
易知,|AB’| = |AB|,|B’F’| = |BF|。同时,因为∠F’AF = 60° ,|AF’| = |AF|,所以三角形AFF’是个等边三角形,所以|FF’| = |AF|。
由上述的等量关系,|AF| + |BF| + |CF| = |FF’| + |B’F’| + |CF|。式子右边的三条线段,即从点C到点B’的三条折线,要使得这三条折线的长度最短,则必须使得B’,F’,F和C四点共线,即F点必须存在于B'C两点之间的线段之上!
如果我们用相同的方法旋转三角形BCF,那么将得到另外一条线段,此线段和B’C的交点,即为该三角形的费马点。
如果我们把B和B’连接起来,就可以发现三角形ABB’正是从边AB向外所作的等边三角形;如果同样对BC和CA作出等边三角形,那么这正是向外拿破仑三角形的做法。根据拿破仑三角形的特性1),三线交于一点,对于单个内角不超过120度的三角形来说,此点正是费马点F。
那么,为什么要加一个单个内角不超过120度的限制?这是因为当三角形ABC中某个内角超过120度时,上述旋转方法得到的点将位于该顶点之外,四点已经无法共线,如下图所示。
设∠BAC > 120°,旋转得到B’,因为∠B’AB = 60°,所以∠BAC + ∠B’AB > 180°,B’点位于直线AC下方;而存在于三角形内部的F点必然位于直线AC另一侧。因此我们无法简单地通过连接B'C,得到一条经过B’,F’,F和C的直线。要使得这三条折线的长度和最短,F只能尽可能地靠近A点,直至和A点重合。
因此,对于单一内角大于120度的三角形,其费马点就是该钝角的顶点。当然,对于这样的三角形来说,拿破仑三角形的几个特性依然有效,只不过三线相交的那个点将位于三角形之外,也不是与原三角形顶点距离之和最小的费马点了。
从费马所处的十七世纪直至拿破仑所处的十九世纪,法国的科学技术得到了迅猛的发展,逐渐取代英国成为当时世界科学的中心,这个时期法国涌现出了伏尔泰、狄德罗这样的思想家,也拥有蒙日、傅里叶、拉普拉斯、拉格朗日、拉瓦锡、居维叶这样的科学家。法国科学的发展,与拿破仑重视科技和教育是分不开的。
除了重视法兰西研究院、与科学家保持密切私交、鼓励发明和创新以外,拿破仑还建立和恢复了不少高等院校,比如巴黎综合理工学校。传说中 ,1814年反法联军兵临巴黎,巴黎综合理工的师生向拿破仑请战,要求上前线保卫巴黎。拿破仑拒绝了他们的请求,说:“我不愿为取金蛋杀掉我的老母鸡!”后来,这句话被镌刻在学校会议室的一座铜钟的底座上,并且在学校的一幅拿破仑肖像的相框上也写上了Poule aux Oeufs d’Or,即“生金蛋的鸡”。
最后的金蛋,哦不,彩蛋:拿破仑关于厄尔巴岛的名言在英文翻译中是一句有趣的回文,你发现了吗?
文/Athlon_BE
2019.7.5