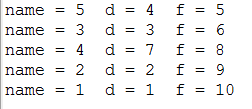前言
图的搜索指的是系统化地跟随图中的边来访问图中每一个结点,并不是随意地访问图中的结点。图的搜索算法可以用来发现图的结构,许多图的算法都要求先搜索全图,可以说,图的搜索是整个图算法的核心。
图的搜索有两种类型:
- 广度优先搜索
- 深度优先搜索
本文中将用到两个图,一个有向图,一个无向图,分别如下:
广度优先搜索
广度优先搜索是指:给定图 G = (V, E)和一个可识别的源结点s,对图中的边进行探索,找到s能到达的所有结点。
举例说明,给定结点s,v为s能到达的所有结点的集合,先寻找s能到达的所有结点,再找集合v中结点能到达的所有结点。
队列和栈有什么不同呢?它们的不同或者说精髓用法体现在图的搜索上,细细体会就能理解队列和栈的精髓。广度优先搜索需要用到队列,因为先找s能到的顶点,再找v集合能到的顶点,需要先入先出,否则就不是广度优先搜索了
邻接链表下的广度优先搜索:
/*
* 广度优先算法
* 广度优先算法可以计算出到遍历起点的最短路径,因为最短路径一定是此顶点的前驱距离+1得到的
* 有权值的后续讨论,如果无权图这个结论是对的
*/
public void bfs(Vertex vertex){
if (vertex == null) {
return;
}
for (Vertex v : mList) {
v.color = COLOR.WHITE;
}
int dis = 0;
int index = mList.indexOf(vertex);
if (index == -1) {
System.out.println("error vertex");
return;
}
Queue queue = new LinkedBlockingDeque();
queue.add(vertex);
vertex.color = COLOR.GRAY;
vertex.d = dis;
System.out.println(vertex);
Arc arc = null;
Vertex temp = null;
while (!queue.isEmpty()) {
temp = queue.peek();
arc = temp.firstArc;
while (arc != null) {
if (arc.vertex.color == COLOR.WHITE) {
arc.vertex.color = COLOR.GRAY;
arc.vertex.d = temp.d + 1;
System.out.println(arc.vertex);
queue.add(arc.vertex);
break;
}
arc = arc.next;
}
if (arc == null) {
temp.color = COLOR.BLACK;
queue.remove(temp);
}
if (queue.isEmpty()) {
for (Vertex vertex2 : mList) {
if (vertex2.color == COLOR.WHITE) {
queue.add(vertex2);
vertex2.color = COLOR.GRAY;
System.out.println(vertex2);
break;
}
}
}
}
}
结点中包含颜色,通过颜色判断结点是否被访问。先将第一个节点V添加到队列,再遍历以V为起点的链表,如果链表中有某个结点未被染色,则访问并添加到队列当中,当以V为起点的链表的所有结点均已被染色,则将V从队列中移除。
特别值得一提的是,广度优先搜索的副产品非常有用,它能够计算最短路径。假设结点V的前驱结点是S,那么到某个点的最短路径V.d = S.d + 1。
δ(s,v),表示s到v的最短距离。u.π表示u的前驱,所以上述算法中的u.d就等于到搜索起点的最短距离。
再看看邻接矩阵情况下的广度优先搜索算法:
public void bfs(Vertex vertex){
if (vertex == null) {
return;
}
int index = mList.indexOf(vertex);
if (index == -1) {
return;
}
for (Vertex v : mList) {
v.color = COLOR.WHITE;
}
Queue queue = new LinkedBlockingDeque<>();
queue.add(vertex);
vertex.color = COLOR.GRAY;
vertex.d = 0;
System.out.println(vertex);
Vertex temp = null;
while (!queue.isEmpty()) {
temp = queue.peek();
int tempIndex = mList.indexOf(temp);
for (int i = 0; i < maxLength; i++) {
if (mEdges[tempIndex][i] != null && mEdges[tempIndex][i].v2.color == COLOR.WHITE) {
mEdges[tempIndex][i].v2.color = COLOR.GRAY;
mEdges[tempIndex][i].v2.d = temp.d + 1;
System.out.println(mEdges[tempIndex][i].v2);
queue.add(mEdges[tempIndex][i].v2);
}
}
queue.remove(temp);
}
}
邻接矩阵下的广度优先搜索变化也不大,主要在寻找结点v有边相连的未被访问的结点逻辑上,稍有不同。
深度优先算法
深度优先搜索,顾名思义,只要可能就在图中尽量深入。深度优先搜索,总是对最近才发现的结点v的出发边进行搜索。
深度优先搜索有两种写法,本文中采用递归方式,不使用栈方法,有兴趣的同学们自己尝试使用栈实现。
邻接链表情况下的深度优先搜索:
int time = 0;
/*
* 深度优先算法,下面的深度优先算法是最正确的,以栈来实现深度优先算法有可能有问题
* 下面的计算方法最容易理解,访问完自己后立即访问自己的非访问后续结点
* 同时深度优先算法,可以计算每个结点访问顺序,最终实现拓扑排序。
* 即f最大的,放在前面
*/
public void dfs(){
for (Vertex vertex : mList) {
vertex.color = COLOR.WHITE;
}
time = 0;
for (Vertex vertex : mList) {
if (vertex.color == COLOR.WHITE) {
dfsVisit(vertex);
}
}
}
public void dfsVisit(Vertex vertex){
if (vertex == null) {
return;
}
time++;
vertex.color = COLOR.GRAY;
vertex.d = time;
Arc arc = vertex.firstArc;
while (arc != null) {
if (arc.vertex.color == COLOR.WHITE) {
dfsVisit(arc.vertex);
}
arc = arc.next;
}
time++;
vertex.f = time;
System.out.println(vertex);
vertex.color = COLOR.BLACK;
}
深度优先搜索,先取顶点数组中的每一个顶点,如果顶点未被访问,则继续访问与该顶点有边相连的顶点,再递归访问新的顶点。
当一个顶点被访问时,它的颜色为灰色,只有当与它相连的所有顶点都被访问完成了,此顶点颜色被置为黑色。
颜色为灰色时,记录时间,颜色为黑色时再次记录时间,将时间打印下来,非常有意思,因为打印的结果就是拓扑排序结果。
拓扑排序是针对有向无环图的概念。举例说明,穿袜子和穿鞋子是图的两个顶点,穿袜子指向穿鞋子,日常生活中一定要先穿袜子才能穿鞋子,这就是拓扑排序干的活。
如果v1和v2有边相连,并且是由v1指向v2,那么一定要先访问v1,再来访问v2。针对前言中的有向图,拓扑排序的结果是 1 2 4 3 5,即f值最大的应该先访问。
邻接矩阵情况下的深度优先搜索:
public void dfs(){
for (Vertex v : mList) {
v.color = COLOR.WHITE;
}
for (Vertex v : mList) {
if (v.color == COLOR.WHITE) {
dfsVisit(v);
}
}
}
int time = 0;
public void dfsVisit(Vertex vertex){
time++;
vertex.color = COLOR.GRAY;
vertex.d = time;
int index = mList.indexOf(vertex);
Vertex v2 = null;
for (int i = 0; i < maxLength; i++) {
v2 = mEdges[index][i] == null ? null : mEdges[index][i].v2;
if (v2 != null && v2.color == COLOR.WHITE) {
dfsVisit(v2);
}
}
time++;
vertex.color = COLOR.BLACK;
vertex.f = time++;
System.out.println(vertex);
}
和邻接链表类似,不再详述
结语
图的两种搜索比较简单,但搜索过程中的额外两个信息是非常重要的。广度优先搜索能够查找最短路径,而深度优先搜索结果中,可以知道拓扑排序结果,f值最大先访问,即是拓扑排序结果。