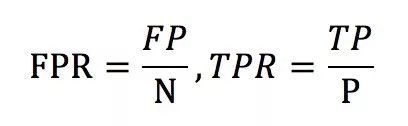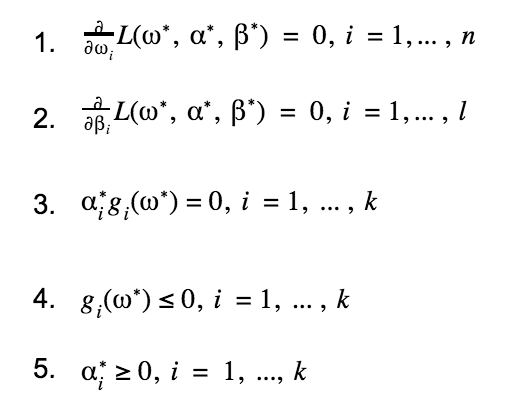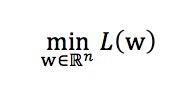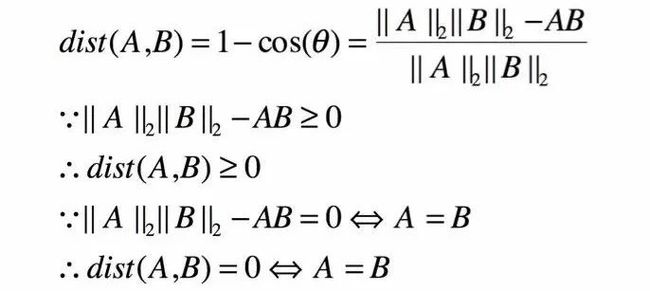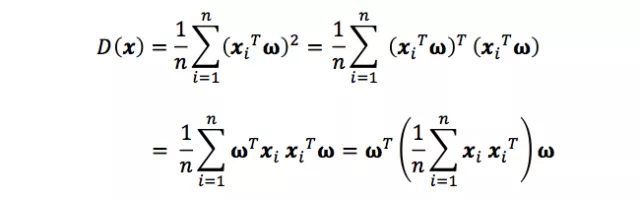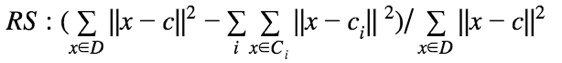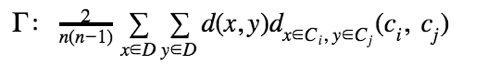转载自https://mp.weixin.qq.com/s/3NtfHjgfhxbf6sVKleoRpA
1. 模型评估
在一个二值分类问题中,如何绘制模型的ROC曲线并计算相应的AUC值?
ROC曲线相比PR(Precision-Recall)曲线有什么优点?
【问题背景】
二值分类器(binaryclassifier)是机器学习领域中最常见也是应用最为广泛的分类器。评价二值分类器的指标很多,比如precision,recall,F-score,PR曲线等,相比较而言,基于ROC曲线的AUC值有很多突出的优点(本题第二问会做相关解释),经常作为评估二值分类器最重要的指标之一。下面我们详细解答一下这道面试题。
【解答】
ROC曲线的全称是theReceiver Operating Characteristic曲线,中文名为“受试者工作特征曲线”。AUC全称是Area under the Curve,曲线下面积,这里的“曲线”一般就是指ROC曲线。所以这道面试题第一问的重点就绘制出ROC曲线,基于ROC曲线计算面积的方法是显然的。
ROC曲线的横坐标为falsepositive rate(FPR),中文一般称为假阳性率,纵坐标为truepositive rate(TPR),中文一般称为真阳性率。FPR和TPR的计算方法如下:
上式中,P指的是所有样本中,真正的正样本的数量,N指的是真正的负样本的数量。TP指的是P个正样本中,分类器把其中TP个预测为正。FP指的是,N个负样本中,分类器把其中FP个样本误判成了正样本。
只看定义确实有点绕,为了更直观的说明这个问题,我们举一个医院诊断病人的例子。假设有10位疑似癌症患者,其中有3位很不幸确实患了癌症(P=3),另外7位不是癌症患者(N=7)。医院对这10位疑似患者做了诊断,也确实发现了3位患了癌症,但这3位患者中,只有2位是真正的患者(TP=2)。那么真阳性率TPR=TP/P=2/3。而对于7位非癌症患者来说,有一位很不幸被误诊为癌症患者(FP=1),那么假阳性率FPR=FP/N=1/7。对于“医院”这个分类器来说,这组分类结果就对应ROC曲线上的一个点(1/7,2/3)。那么ROC曲线上的其他点都是怎样生成的呢?
事实上,ROC曲线是通过不断移动分类器的“截断点”来生成所有关键点的,我们通过下面的例子来解释“截断点”的概念。
在一个二值分类问题中,我们构建的模型输出一般都是预测样本为正例的概率。假设我们的测试集中有20个样本,模型的输出如下图所示,图中第一列为样本序号,Class为样本的真实标签,Score为模型输出的样本为正的预测概率,样本按照预测概率从高到低排序。
图片来自Fawcett,Tom. "An introduction to ROC analysis." Pattern recognition letters27.8 (2006): 861-874.
在预测样本为正负例的时候,我们需要指定一个阈值。大于等于这个阈值的样本都会预测为正样本。比如指定0.9为阈值,那么只有第一个样本会被预测为正例,其他全部都是负例。上面所说的“截断点”指的就是区分正负预测结果的阈值。我们动态调整这个截断点,从最高的得分开始(实际是从正无穷开始开始,对应着ROC曲线的零点),逐渐调整到最低得分,每一个截断点都会对应一个FPR和TPR,在ROC图上绘制出每个截断点对应的位置,再连接每个点即得到最终的ROC曲线。
就本例来说,当截断点选择为正无穷时,模型把全部样本预测为负例,那么FP和TP必然都为0,FPR和TPR也都为0,显然,曲线的第一个点就是(0,0)。当把截断点调整为0.9时,模型预测1号样本为正样本,并且该样本确实是正样本,因此,TP=1,20个样本中,所有正例数量为P=10,故TPR=TP/P=1/10;这里没有预测错的正样本,即FP=0,负样本总数N=10,故FPR=FP/N=0/10=0。对应着ROC图上的点(0,0.1),依次调整截断点,直到画出全部的关键点,再连接关键点即得到了下图所示的ROC曲线。
图片来自Fawcett, Tom. "An introduction to ROCanalysis." Pattern recognition letters 27.8 (2006): 861-874.
其实,绘制ROC曲线有一个更直观的方法,我们首先根据样本标签统计出正负样本的数量,假设正样本数量为P,负样本数量为N。下一步就把横轴的刻度间隔设置为1/N,纵轴的刻度间隔设置为1/P。再根据模型预测结果将样本进行排序后,从高到低遍历样本,与此同时从零点开始绘制ROC曲线,每遇到一个正样本就沿纵轴正方向绘制一个单位长度的曲线,每遇到一个负样本就延横轴正方向绘制一个单位长度的曲线,直到遍历完所有样本,曲线也最终终结在(1,1)这个点。
有了ROC曲线,计算AUC只要沿着横轴做积分就可以了。由于ROC曲线一般都处于y=x这条直线的上方(如果不是的话,只要把模型预测的概率反转成1-p就可以得到一个更好的分类器),所以AUC的取值一般在0.5和1之间。显然,AUC越大,分类器越可能把真正的正样本排在前面,分类器性能越好。
ROC曲线相比PR(Precision-Recall)曲线有什么优点?
除了ROC曲线外,还有很多评估分类模型的指标,PR曲线也是经常使用的指标之一。与ROC曲线不同的是,PR曲线的横坐标是Recall,纵坐标是Precision。
ROC曲线相比PR曲线有一个非常好的特性:就是当正负样本分布发生变化的时候,ROC曲线的形状能够基本保持不变。而PR曲线的形状会发生较剧烈的变化。
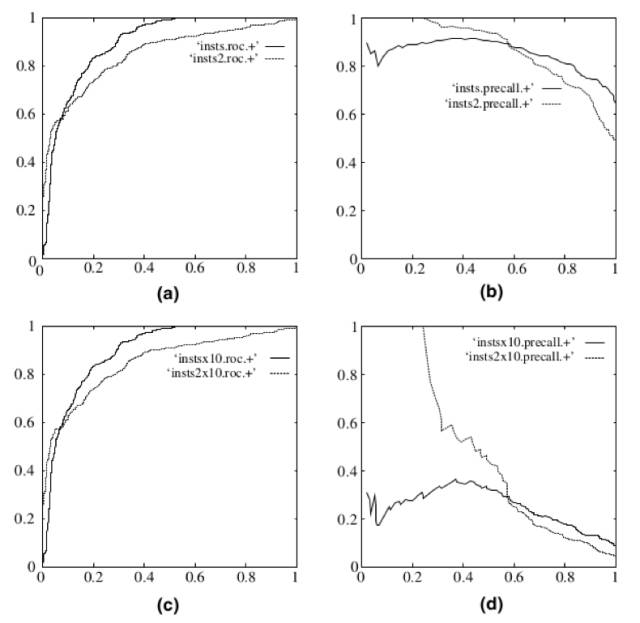
图片来自Fawcett, Tom. "An introduction to ROCanalysis." Pattern recognition letters 27.8 (2006): 861-874.
举例来说,上图是ROC曲线和PR曲线的一张对比图,左边两幅是ROC曲线,右边两幅是PR曲线。下面两幅图是将测试集的负样本数量增加10倍后的结果。可以明显看出,PR曲线发生了明显的变化,而ROC曲线形状基本不变。这就让ROC曲线能够尽量屏蔽测试集选择带来的干扰,更加客观的衡量模型本身的性能。
这样的优点有什么实际意义呢?因为在很多实际问题中,正负样本数量往往很不均衡,比如计算广告领域经常涉及的转化率模型,正样本的数量往往是负样本数量的1/1000甚至1/10000,这个时候选择不同的测试集,PR曲线的变化就会非常大,这显然不利于评估模型本身的性能。而ROC曲线则能够更加稳定的反应模型本身的好坏,适用的场景更多,广泛适用于排序、推荐、广告等领域。
2. SVM模型
在空间上线性可分的两类点,分别向SVM分类的超平面上做投影,这些点在超平面上的投影仍然是线性可分的吗?
能否证明你的观点?
【解答与分析】
首先分析题意,线性可分的两类点,即指通过一个超平面可以将两类点完全分开,如左图所示,假设蓝色的超平面(对于二维空间来说,一维的线即为超平面)为SVM算法计算得出的分类平面,那么红绿两类的点就被它完全分开。我们的问题是将红绿两色的点,向蓝色平面上做如右图所示投影,可得在超平面上红绿两色的点,问题即为投影后的点仍然是线性可分的吗?
这个问题初看起来第一感觉是并不是线性可分的,反例也很好构造,设想只有两个点每个点各属于一类的情况,那么SVM的分类超平面就在两点连线的中垂线上,那么两点关于超平面的投影落在了平面上的同一点自然无法线性可分。实际上对于任意线性可分的两组点,它们在SVM分类的超平面上的投影都是线性不可分的,那么这个结论怎么证明呢?
我们在下面的叙述中以二维情况进行讨论,对于高维空间的推广也是成立的。先考虑SVM分类中只有支持向量的情况,使用反证法,假设存在一个SVM分类结果的超平面,所有支持向量在这个超平面上的投影依然线性可分。那么这个超平面的分类结果如下图所示,使用初等几何知识不难发现图中A,B两点连线的中垂线所组成的超平面蓝色虚线是相较于蓝色实线超平面更优的解,且两组点在新的超平面下线性不可分。而我们之前假设蓝色实线超平面为最有的解,由此推出矛盾。
但我们的证明目前还有不严谨之处,即我们假设了仅有支持向量的情况,会不会在超平面的变换过程支持向量发生了改变,原先的非支持向量和支持向量发生了转化呢?下面我们就来证明SVM的分类结果仅依赖于支持向量。考虑SVM推导中的KKT条件:
结合3和4两个条件不难发现gi()<0时,必有i=0,将这一结果与拉格朗日对偶优化问题的公式相比较:
可以看到,除支持向量外,其他非支持向量的系数均为0,所以SVM的分类结果与仅使用支持向量的分类结果一致,这也是SVM有极高的运行效率的关键之一。将这一结论代回我们的假设中,可知去掉非支持向量并不影响SVM的分类结果,故此证明成立。
实际上,该问题也可以通过凸优化理论中的超平面分离定理(Separating Hyperplane Theorem)更加轻巧地解决。该定理是在凸优化理论中极为重要,定理的定义是:对于不相交的两个凸集,存在一个超平面,将两个凸集分离,并且该超平面为两个凸集上最短距离两点连线的中垂线。
我们可以考虑线性可分的这两类点的凸包,不难发现,SVM所求得的超平面为两凸包上最短距离两点连线的中垂线,由超平面分离定理可得,其为定理中两类点的凸包的超平面。而两个凸包中距离最短的两点只有两种可能,为样本点或在两个样本点的连线上。分情况两边均为样本点,两边均在样本点的连线上,一边为样本点一边在样本点的连线上三种情况简单讨论即可发现,无论哪种情况两类点的投影均是线性不可分的。
对于面试者来说,能通过对SVM的推导给出前一种结论即可,如果熟悉凸优化理论,也可以根据后一种思路来作答。
【拓展阅读】
SVM的公式推导过程:
http://cs229.stanford.edu/notes/cs229-notes3.pdf
对偶问题与KKT条件:
http://stanford.edu/class/ee364a/lectures/duality.pdf
超平面分离定理:
http://www.princeton.edu/~amirali/Public/Teaching/ORF523/S16/ORF523_S16_Lec5_gh.pdf
3. 优化简介
引言
优化是应用数学的一个分支,也是机器学习的核心组成部分。有文章[1] 认为,
机器学习算法 =模型表征+ 模型评估+ 优化算法
其中优化算法所做的事情就是在模型假设空间中找到模型评估指标最好的模型。不同的模型假设、不同的评估指标,对应的优化算法都不尽相同,例如经典的SVM(线性分类模型+ 最大间隔)、逻辑回归(线性分类模型+ 交叉熵)、CART(决策树模型+ 基尼纯度)等。
随着大数据和深度学习的迅猛发展,在实际应用中我们面临的大多是大规模、高度非凸的优化问题,这给传统的基于全量数据、凸优化的优化理论带来巨大的挑战。如何设计适用于新场景的高效、准确的优化算法成为近年来的研究热点。虽然优化是一门能够追溯到拉格朗日、欧拉的“古老”学科,但是大部分能够用于训练深度神经网络的优化算法直到最近几年才被提出,例如Adam算法[2] 等。
目前大部分机器学习工具已经内置了常用的优化算法,所以我们实际只需要一行代码即可完成调用,省去了实现的烦恼。但鉴于优化算法在机器学习中的重要作用,我们认为了解优化算法的原理还是很有必要的,也许在解决实际问题的过程中你也能提出更好的求解算法呢。
我们从一道简单的题开始这段激动人心的优化之旅吧。
“梯度验证”
场景描述
为了求解一个优化问题,最重要的操作是计算目标函数的梯度。在一些机器学习的应用中,例如深度神经网络,目标函数的梯度公式非常复杂,需要验证自己写出的实现代码是否正确。
问题描述
假设你需要求解优化问题
并且用代码实现了求目标函数值和求目标函数梯度的功能。问如何利用求目标函数值的功能来验证求目标函数梯度的功能是否正确?
先验知识
线性代数,微积分
解答和分析
参考文献
[1] Domingos, Pedro. "A few useful things to know aboutmachine learning." Communications of the ACM 55.10 (2012): 78-87.
[2] Kingma, Diederik, and Jimmy Ba. "Adam:A method for stochastic optimization." arXiv preprint arXiv:1412.6980(2014).
4. 采样
引言
古人有云:“知秋一叶,尝鼎一脔”,其中蕴含的就是采样思想。采样,就是根据特定的概率分布产生对应的样本点。对于一些简单的分布(如均匀分布、高斯分布),很多编程语言里面都有直接的采样函数。然而,即使是这种简单的分布,其采样过程也并不是显而易见,需要精心设计;对于比较复杂的分布,往往并没有直接的采样函数可供调用,这时候就需要其它更加复杂的采样方法。因此,对采样方法的深入理解是很有必要的。
采样在机器学习中有着重要的应用,它可以将复杂的分布简化为离散的样本点,可以对样本集进行调整(重采样)以更好地适应后续的模型学习,或者用于随机模拟以进行复杂的模型求解。
在“采样”这个系列中,我们会通过不同的问题与解答,来展现机器学习中的采样知识,包括采样方法(直接采样、接受/拒绝采样、重要性采样、MonteCarlo采样等)、采样的应用,以及采样在一些算法中的具体实现。今天,我们以采样在训练数据不均衡时的应用来开始我们的“采样”系列。
“不均衡样本集的处理”
场景描述
在训练二分类模型时,经常会遇到正负样本不均衡的问题,例如医疗诊断、网络入侵检测、信用卡反诈骗等。对于很多分类算法,如果直接采用不均衡的样本集来进行训练学习,会存在一些问题。例如,如果正负样本比例达到1:99,则分类器简单地将所有样本都判为负样本就能达到99%的正确率,显然这并不是我们想要的,我们想让分类器在正样本和负样本上都有足够的准确率和召回率。
问题
对于二分类问题,当训练集中正负样本非常不均衡时,如何处理数据以更好地训练分类模型?
背景知识:机器学习,概率统计
解答与分析
为什么很多分类模型在训练数据不均衡时会出现问题?本质原因是模型在训练时优化的目标函数和人们在测试时使用的评价标准不一致。这种“不一致”可能是由于训练数据的样本分布与测试时期望的样本分布不一致,例如,在训练时优化的是在整个训练集(正负样本比例可能是1:99)上的正确率,而测试时可能想要模型在正样本和负样本上的平均正确率尽可能大(实际上是期望正负样本比例为1:1);也可能是训练阶段不同类别的权重(重要性)与测试阶段不一致,例如训练时认为所有样本的贡献是相等的,而测试时 False Positive和False Negative有着不同的代价。
根据上述分析,一般可以从两个角度来处理样本不均衡问题:
1)基于数据的方法:主要是对数据进行重采样,使原本不均衡的样本变得均衡。
直接的随机采样虽然可以使样本集变得均衡,但会带来一些问题:过采样对少数类样本进行了多次复制,扩大了数据规模,增加了模型训练的复杂度,同时也容易造成过拟合;欠采样会丢弃一些样本,可能会损失部分有用信息,造成模型只学到了整体模式的一部分。
SMOTE算法为每个少数类样本合成相同数量的新样本,这可能会增大类间重叠度,并且会生成一些不能提供有益信息的样本。为此出现Borderline-SMOTE、ADASYN等改进算法:Borderline-SMOTE只给那些处在分类边界上的少数类样本合成新样本,而ADASYN则给不同的少数类样本合成不同个数的新样本。此外,还可以采用一些数据清理方法(如基于TomekLinks)来进一步降低合成样本带来的类间重叠,以得到更加well-defined的类簇,从而更好地训练分类器。
SMOTE算法
在实际应用中,具体的采样操作可能并不总是如上述几个算法一样,但基本思路很多时候还是一致的。例如,基于聚类的采样方法,利用数据的类簇信息来指导过采样/欠采样操作;经常用到的数据扩充 (data augmentation) 方法也是一种过采样,对少数类样本进行一些噪音扰动或变换(如图像数据集中对图片进行裁剪、翻转、旋转、加光照等)以构造出新的样本;而Hard Negative Mining则是一种欠采样,把比较难的样本抽出来用于迭代分类器。
2)基于算法的方法:在样本不均衡时,也可以通过改变模型训练时的目标函数(如代价敏感学习中不同类别有不同的权重)来矫正这种不平衡性;当样本数目极其不均衡时,也可以将问题转化为one-class learning / anomalydetection。本节主要关注采样,不再细述这些方法(我们会在其它章节的陆续推送相关知识点)。
扩展与总结
在实际面试时,这道题还有很多可扩展的知识点。例如,模型在不均衡样本集上的评价标准(可以参考“Hulu机器学习问题与解答系列”的第一弹:模型评估);不同样本量(绝对数值)下如何选择合适的处理方法(考虑正负样本比例为1:100和1000:100000的区别);代价敏感学习和采样方法的区别、联系以及效果对比等。
5. 余弦距离
场景描述
在机器学习中,我们常将特征表示为向量的形式。在近年来,将高维稀疏的研究对象表示为低维分布的向量形式,极大地提高了各类模型的效果。在分析两个向量之间的相似性时,常使用余弦相似度来表示。余弦相似度的取值范围是[-1,1],相同的两个向量之间的相似度为1。如果希望得到类似于距离的表示,将1减余弦相似度即为余弦距离。余弦距离的取值范围为[0,2],相同的两个向量余弦距离为0。
问题
1. 结合你的学习和研究经历,探讨为什么要在一些场景使用余弦相似度而不是欧式距离?
2. 余弦距离是否是一个严格定义的距离?
先验知识:基本数学
解答与分析
问题1: 该题考查对余弦相似度和欧氏距离的理解和区分,以及对它们的使用经验。
余弦相似度关注的是两个向量之间的角度关系,而并不关心它们的绝对大小,其取值范围是[-1,1]。当我们比较两个长度差距很大、但内容相近的文本的相似度时,如果使用词频或词向量作为特征,那么欧式距离会很大;而如果使用余弦相似度,其夹角很小,因而相似度很高。
此外,在文本,图像,视频等领域,研究的对象特征维度往往很高,余弦相似度在高维的情况下,依然保持相同时为1,正交时为0,相反时为-1的性质;而欧式距离的数值受到维度的影响,范围不固定,并且其含义会比较模糊。
在一些场景例如word2vec中,其向量的模长是固定的,此时欧氏距离与余弦相似度有着单调的关系,即欧氏距离:
在此场景下,如果选择距离最小/相似度最大的近邻,那么使用余弦相似度和欧氏距离,其结果是相同的。
这道题同时要考察被试者的研究和学习经历,初学者可以从两者的定义开始拓展讨论,余弦相似度更适用于向量模长不相等的场景中;研究者如果是NLP背景的,可以结合词、文本的各种表示,以及如何求其相似度等问题进行探讨;如果是CV背景的,可以结合HOG特征的使用、人脸识别等场景进行探讨。总而言之,特定的度量方法适用于什么样的问题,需要在学习和研究中多总结和思考,这样不仅仅对面试有帮助,在遇到新的问题时,也可以活学活用。
问题2: 该题考察对距离的定义的理解,以及简单的反证和推导。
余弦距离不是严格定义的距离。
在一个集合中,如果每一对元素均可唯一确定一个实数,使得三条距离公理(正定性,对称性,三角不等式)成立,则该实数就可称为这对元素之间的距离。
余弦距离满足正定性和对称性,但是不满足三角不等式。对于向量A,B:
1: 正定性
2: 对称性
3: 三角不等式
下面给出一个反例:
给定A=(1,0), B=(1,1), C=(0,1) 那么:
假如面试的时候紧张,一时想不到反例,该怎么办呢?
此时可以思考余弦距离和欧式距离的关系,从题1中,我们知道单位圆上欧式距离和余弦距离满足:
显然在单位圆上,余弦距离和欧氏距离的范围都是[0,2]。我们已知欧式距离是一个合法的距离,而余弦距离与欧式距离有二次关系,那么自然不满足三角不等式。可以假设A与B、B与C非常近,其欧式距离为极小量u;此时A、B、C虽然在圆弧上,但近似在一条直线上,所以A与C的欧式距离接近于2u。因此,A与B、 B与C的余弦距离为1/2u2;A与C的余弦距离接近于2u2,大于A与B、B与C的余弦距离之和。
假如遇到这种类型的题该怎么办呢?首先,大多数应试者未必能熟记距离三公理,这没有关系,应该主动和面试官沟通合法距离的定义。然后,正定性和对称性的证明,只是给出含糊的表述诸如‘显然满足’是不好的,应该给出一些推导。最后,三角不等式的证明/证伪中,不应表述为‘我觉得满足/不满足’,而是应该积极分析给定三个点的情况,或者推导其和欧式距离的关系,这样哪怕一时找不到反例而误认为其是合法距离,也比‘觉得不满足’这样蒙对正确的答案要好。
笔者首次注意到余弦距离不符合三角不等式,是在研究电视剧的标签时,发现在通过影视语料库训练出的词向量中,comedy(喜剧)和funny,funny和happy的余弦距离都很近,小于0.3,然而comedy和happy的余弦距离却高达0.7。这一现象明显不符合距离的定义,引起了我们的注意和讨论,经过思考和推导,得出了上述结论。
在机器学习领域,被俗称为距离,却不满足三条距离公理的不仅仅有余弦距离。KL距离(又被称为KL散度、相对熵)也是一例,它常被用于计算两个分布之间的差异,不满足对称性和三角不等式。
6. 降维
引言
宇宙,是时间和空间的总和。时间是一维的,而空间的维度,众说纷纭,至今没有定论。弦理论说是9维,霍金所认同M理论则认为是10维。它们解释说人类所能感知的三维以外的维度都被卷曲在了很小的空间尺度内。当然,谈及这些并不是为了推销《三体》系列读物,更不是引导读者探索宇宙真谛,甚至怀疑人生本质,而是为了引出今天机器学习课堂主题——降维。
机器学习中的数据维数与现实世界的空间维度本同末离。在机器学习中,数据通常需要被表示成向量形式以输入模型进行训练。但众所周知,对高维向量进行处理和分析时,会极大消耗系统资源,甚至产生维度灾难。例如在CV(计算机视觉)领域中将一幅100x100的RGB图像提取像素特征,维度将达到30000;在NLP(自然语言处理)领域中建立<文档-词>特征矩阵,也动辄产生几万维的特征向量。因此,进行降维,即用一个低维度的向量表示原始高维度的特征就显得尤为重要。试想,如果宇宙真如M理论所说,每个天体的位置都由一个十维坐标来描述,应该没有一个正常人能想象出其中的空间构造。但当我们把这些星球投影到一个二维平面,整个宇宙便会像上面的银河系一样直观起来。
常见的降维方法主要有主成分分析(PCA)、线性判别分析(LDA)、等距映射(Isomap)、局部线性嵌入(LLE)、拉普拉斯特征映射(LE)、局部保留投影(LPP)等。这些方法又可以按照线性/非线性,监督/非监督,全局/局部,进行不同划分。其中 PCA作为最经典的方法,至今已有100多年的历史,它属于一种线性、非监督、全局的降维算法。我们今天就来回顾一下这经久不衰的百年经典。
“PCA”
场景描述
在机器学习领域中,我们对原始数据进行特征提取,有时会得到比较高维的特征向量。在这些向量所处的高维空间中,包含很多的冗余和噪声。我们希望通过降维的方式来寻找数据内部的特性,从而提升特征表达能力,降低训练复杂度。PCA(主成分分析)作为降维中最经典的方法,是面试中经常被问到的问题。
问题
PCA的原理及目标函数
PCA的求解方法
背景知识:线性代数
解答与分析
PCA(principal components analysis), 即主成分分析,旨在找到数据中的主成分,并利用这些主成分表征原始数据,从而达到降维的目的。举一个简单的例子,在三维空间中有一系列数据点,这些点分布在一个过原点的平面上。如果我们用自然坐标系x, y, z这三个轴来表示数据,需要使用三个维度,而实际上这些点只出现在一个二维平面上,如果我们通过坐标系旋转使得数据所在平面与x, y平面重合,那么我们就可以通过x’, y’两个维度表达原始数据,并且没有任何损失,这样就完成了数据的降维,而x’, y’两个轴所包含的信息就是我们要找到的主成分。
但在高维空间中,我们往往不能像刚才这样直观地想象出数据的分布形式,也就更难精确地找到主成分对应的轴是哪些。不妨,我们先从最简单的二维数据来看看PCA究竟是如何工作的。
上图(左)是二维空间中经过中心化的一组数据,我们很容易看出主成分所在的轴(以下称为主轴)的大致方向,即右图中绿线所处的轴。因为在绿线所处的轴上,数据分布的更为分散,这也意味着数据在这个方向上方差更大。在信号处理领域中我们认为信号具有较大方差,噪声具有较小方差,信号与噪声之比称为信噪比,信噪比越大意味着数据的质量越好。由此我们不难引出PCA的目标,即最大化投影方差,也就是让数据在主轴上投影的方差最大。
熟悉线性代数的读者马上就会发现,原来,x投影后的方差就是协方差矩阵的特征值。我们要找到最大的方差也就是协方差矩阵最大的特征值,最佳投影方向就是最大特征值所对应特征向量。次佳投影方向位于最佳投影方向的正交空间中,是第二大特征值对应的特征向量,以此类推。至此,我们得到了PCA的求解方法:
总结与扩展
至此,我们从最大化投影方差的角度解释了PCA的原理、目标函数和求解方法,其实PCA还可以用其他思路(比如最小回归误差的角度)进行分析,得到新的目标函数,但最终会发现其对应的原理和求解方法与本文中的是等价的。另外,由于PCA是一种线性降维方法,虽然经典,但其具有一定局限性。我们可以通过核映射对PCA进行扩展得到KPCA方法,也可以通过流形映射的降维方法(如Isomap、LLE、LE等)对一些PCA效果不好的复杂数据集进行非线性降维操作。这些方法都会在之后的推送中有所涉及,敬请期待。
7.非监督学习算法与评估
场景描述
人具有很强的归纳思考能力,善于从一大堆碎片似的事实或者数据中寻找普遍规律,并得到具有逻辑性的结论。以用户观看视频的行为为例,可以存在多种直观的归纳方式,比如从观看内容的角度看,有喜欢看动画片的,有喜欢看偶像剧的,有喜欢看科幻片的等等;从使用设备的角度看,有喜欢在台式电脑上观看的,有喜欢手机或者平板便携式设备上观看的,还有喜欢在电视等大屏幕上观看的;从使用习惯上看,有喜欢傍晚观看的,有喜欢中午时段观看的,有每天都观看的用户,也有只在周末观看的用户,等等。对所有用户进行有效的分组对于理解用户并推荐给用户合适的内容是重要的。通常这类问题没有观测数据的标签或者分组信息,需要通过算法模型来寻求数据内在的结构和模式 。
问题
以聚类算法为例,假设没有外部标签数据,如何区分两个无监督学习(聚类)算法性的优劣呢?
背景知识:非监督学习,常见聚类算法
解答与分析
场景描述中的例子就是一个典型的聚类问题,从中可以看出,数据的聚类依赖于需求的定义,同时也依赖于分类数据的特征度量以及数据相似性的方法。相比于监督式学习,非监督学习通常没有正确答案,算法模型的设计直接影响最终的输出和性能,需要通过多次迭代的方法寻找模型的最优的参数。因此了解常见数据簇的特点和常见聚类算法的特点,对寻求评估不同聚类算法性能的方法有很大的帮助。
常见数据簇的特点:
以中心定义的数据簇:这类数据集合倾向于球形分布,通常中心被定义为质心,即此数据簇中所有点的平均值。集合中的数据到中心的距离相比到其它簇中心的距离更近;
以密度定义的数据簇:这类数据集合呈现和周围数据簇明显不同的密度,或稠密或稀疏。当数据簇不规则或互相盘绕,并且有噪声和离群点时,常常使用基于密度的簇定义;
以连通定义的数据簇:这类数据集合中的数据点和数据点之间有连接关系,整个数据簇表现为图结构,该定义对不规则形状或者缠绕的的数据簇有效;
以概念定义的数据簇:这类数据集合中的所有数据点具有某种共同性质。
常见的聚类算法的特点:
划分聚类:将数据对象划分成互不重叠的数据簇,其中每个数据点恰在一个数据簇中;
层次聚类:数据簇可以具有子簇,具有多个(嵌套)子簇的数据簇可以表示为树状结构;
模糊聚类:每个数据点均以0~1的隶属权值属于某个数据簇;
完全/不完全聚类:是否对所有数据点都指派一个数据簇。
由于数据以及需求的多样性,没有一种算法能够适应所有的数据类型、簇和应用,似乎每种情况都可能需要一种不同的评估度量。例如,K均值聚类通常需要用SSE (Sum of Square Error) 来评估,但是基于密度的数据簇可以不必是球形,SSE则完全失效。在许多情况下,判断聚类算法结果的好坏最终强烈依赖主观解释。尽管如此,聚类算法的评估还是必须的,它是聚类分析中重要部分之一 。
对聚类算法优劣的评估通常可以总结为对以下五个方面的分析:
辨识数据中是否存在非随机簇结构的能力;
辨识数据中正确数据簇的能力;
评估数据被正确聚类的能力;
辨识两个数据簇之间优劣的能力;
评估与客观数据集之间的差异;
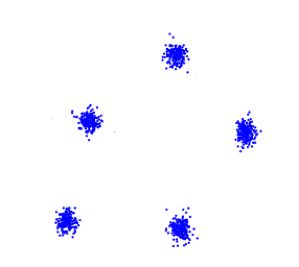
假设存在外部标注数据的支持,那么第5点将转化为监督学习的问题,直接度量聚类算法发现的聚类结构与标注数据的结构匹配程度即可。假设不存在外部标注数据,基于以上所列14点,可以如下图15所示,测试聚类算法对不同类型数据簇的聚类能力:
图1. 观察误差是否随聚类类别数量的增加而单调变化
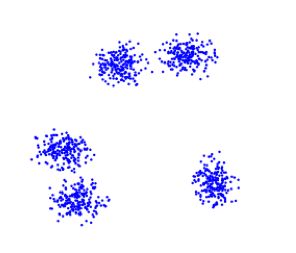
图2. 观察误差对聚类结果的影响
图3. 观察近邻数据簇的聚类准确性
图4. 观察聚类算法在处理较大的数据密度差异时的性能
图5. 观察处理不同大小数据种类时的聚类准确度
扩展问题
在以上的回答中介绍了五种评估两个聚类算法性能优劣的,那么具体而言有哪些常见的指标可以用来计算和辨识聚类算法优劣呢?给出几种可能的数据簇形态,定义评估指标可以展现面试者实际解决和分析问题的能力。事实上测量指标可以有很多种,以下列出了三个在数据紧凑性或数据簇可分离程度上的度量,更多指标则请参考文献[1],具体描述如下:
- 均方根标准偏差 (RMSSTD),衡量聚类同质性:
- R方 (R-Square),衡量聚类差异度:
- 改进的Hubert Γ统计,通过数据对的不一致性来评估聚类的差异:
这其中:
8. 强化学习】
为帮助大家更好地理解本期课题,作者将首先介绍强化学习的基本概念。解答与分析请关注明日推送。
“强化学习的基本概念”
强化学习近年来在机器学习领域越来越火,也受到了越来越多人的关注。强化学习是一个20世纪80年代兴起的,受行为心理学启发而来的一个机器学习领域,它关注身处某个环境中的决策器通过采取行动获得最大化的累积收益。和传统的监督学习不同,在强化学习中,并不直接给决策器的输出打分。相反,决策器只能得到一个间接的反馈,而无法获得一个正确的输入/输出对,它需要在不断的尝试中优化自己的策略以获得更高的收益。从广义上说,大部分涉及动态系统的决策学习过程都可以看成是一种强化学习。它的应用非常广泛,包括博弈论、控制论、优化等多个不同领域。这两年,AlphaGo及其升级版横空出世,彻底改变了围棋这一古老的竞技领域,在业界引起很大震惊,其核心就是强化学习。与未来科技发展密切相关的机器人领域,也是强化学习的用武之地,从机器人行走,到自动驾驶,处处都有强化学习的身影。
强化学习的基本场景可以用下图来描述(图来自于wiki),有环境(Environment)、机器人(Agent),状态(State),动作(Action),奖励(Reward)等几个基本概念。一个机器人在环境中会发出各种动作,环境会接收到动作,引起自身状态的变迁,同时给机器人以奖励。机器人的目标就是使用一些策略,发出合适的动作,最大化自身的收益。
整个场景一般可以描述为一个马尔科夫决策过程(Markov decision process, MDP),这个过程的几个要素如下(这里我们以离散时间的马尔科夫决策过程为例,整个过程也是离散时间随机控制过程):
动作(action),所有可能发出动作的集合记作A(可能是无限的);
状态(state),所有状态的集合记作S;
奖励(reward),机器人可能收到的奖励,一般是一个实数;
强化学习的核心任务是,学习一个从状态空间S到动作空间A的映射,最大化累积受益。常用的强化学习算法有Q学习(Q-Learning),策略梯度(Policy gradient),以及演员评判家算法(Actor-critic)等。
“视频游戏里的强化学习”
场景描述
游戏是强化学习最有代表性也是最合适的应用领域之一,其几乎涵盖了强化学习所有的要素,例如环境:游戏本身的状态,动作:用户操作,机器人:程序,回馈:得分、输赢等。通过输入原始像素来玩视频游戏,是人工智能成熟的标志之一。雅达利(Atari)是20世纪七八十年代红极一时的电脑游戏,类似于国内的红白机游戏,但是画面元素要更简单一些。它的模拟器相对成熟简单,使用雅达利游戏来测试强化学习,是非常合适的。应用场景可以描述为:在离散的时间轴上,每个时刻你可以得到当前的游戏画面,选择向游戏机发出一个指令(上下左右,开火等),然后得到一个回馈(reward)。由于基于原始像素的强化学习对应的状态空间巨大,没有办法直接使用传统的方法。于是,2013年DeepMind提出了深度强化学习模型,开始了深度学习和强化学习的结合[1]。
传统的强化学习主要使用Q-learning,而深度强化学习也使用Q-learning为基本框架,把Q-learning的对应步骤改为深度形式,并引入了一些技巧,例如经验重放(experience replay)来加快收敛以及提高泛化能力。
问题描述
什么是深度强化学习,它和传统的强化学习有什么不同,如何用它来玩视频游戏?
背景知识:强化学习,Q-learning
解答与分析
先来看看经典的Q-learning:
为了能与Deep Q-learning作对比,我们把最后一步换成下面等价的描述:
深度的Q-learning(其中红色部分为和传统Q-learning不同的部分):
不同点主要在子步骤的细节上:
需要注意的是,传统的Q-learning直接从环境观测获得当前状态,而在Deep Q-learning中,往往需要对观测的结果进行某些处理来获得Q函数的输入状态。在用Deep Q-learning玩Atari游戏中,是这样对观察值进行处理的。