若定点运动的刚体所受外力对固定点O的主矩$T=0$,则这种情况称为刚体定点运动的欧拉情况,相应的刚体常称为欧拉陀螺。刚体自由转动时外力矩为零,因此角动量守恒,角动量平方也守恒,即:$$L^2=I^2_1\omega^2_x+I^2_2\omega^2_y+I^2_3\omega^2_z=常数$$
同时它的能量也守恒:$$E=\frac{1}{2}(I_1\omega^2_x+I_2\omega^2_y+I_3\omega^2_z)=常数$$
刚体转动的稳定性是讨论什么条件下刚体的角速度不随时间变化。显然,只有外力矩为零时才有可能,即只有欧拉陀螺才谈得上转动的稳定性。假设刚体惯性矩各不相同,即$I_{zz}>I_{yy}>I_{xx}$,如果刚体在没有外力矩作用下绕其惯性主轴自由转动,在发生微小扰动的情况下转动稳定性是怎样的呢?设刚体初始时刻绕X轴旋转,则角速度可以表达为$\mathbf{\omega}=\omega_x \mathbf{e_x}$,$\mathbf{e_x}$是X轴基向量。在刚体上施加一点微小的扰动,其角速度变为$$\mathbf{\omega}=\omega_x \mathbf{e_x}+\lambda \mathbf{e_y}+\mu\mathbf{e_z}$$
$\lambda$和$\mu$都是很小的量,将角速度带入欧拉方程可得到:$$I_{xx}\dot{\omega}_x-(I_{yy}-I_{zz})\lambda\mu=0\\I_{yy}\dot{\lambda}-(I_{zz}-I_{xx})\omega_x\mu=0 \\I_{zz}\dot{\mu}-(I_{xx}-I_{yy})\omega_x\lambda=0$$
$\lambda\mu$是二阶小的量,因此在方程中可以忽略。因此从上面第一个方程中可以得到X轴角加速度为零,即$\omega_x$近似是恒定值。其他两个方程可以写为:$$\dot{\lambda}=[\frac{(I_{zz}-I_{xx})\omega_x}{I_{yy}}]\mu\\ \dot{\mu}=-[\frac{(I_{yy}-I_{xx})\omega_x}{I_{zz}}]\lambda$$
对上面第一个等式两边对时间求导后带入第二个等式中,消除$\dot{\mu}$可得到一个关于$\lambda$的二阶常系数齐次线性微分方程:$$\ddot{\lambda}+[\frac{(I_{yy}-I_{xx})(I_{zz}-I_{xx})}{I_{yy}I_{zz}}]\omega^2_x\lambda=0$$
显然$\mu$也满足上面的微分方程。根据之前惯性矩大小的设定,方程中方括号的那一项为正值,因此根据二阶常系数齐次线性方程判别式的符号($\Delta=p^2-4q<0$)可知其通解为:$$\lambda=\lambda_0cos(\Omega_xt-\alpha)$$
其中,$\lambda_0$和$\alpha$是常数,且有:$$\Omega_x=[\frac{(I_{yy}-I_{xx})(I_{zz}-I_{xx})}{I_{yy}I_{zz}}]^{1/2}\omega_x$$
从微分方程的解可以看出,刚体会以角频率$\Omega_x$绕其初始状态做正弦振荡。即刚体绕其X轴旋转时,转动在微小扰动的作用下是稳定的,因为扰动角速度$\lambda$的幅值不随着时间增长而放大发散。
如果刚体初始时刻绕着Z轴旋转,并施加了一个微小的扰动。这时情形与绕X轴旋转类似,我们可以写出振荡的角频率:$$\Omega_z=[\frac{(I_{zz}-I_{xx})(I_{zz}-I_{yy})}{I_{xx}I_{yy}}]^{1/2}\omega_z$$
因此,刚体绕Z轴旋转时对微小扰动也是稳定的。
假设刚体绕Y轴旋转,即绕中间惯量轴旋转,受到微小扰动:$\mathbf{\omega}=\lambda \mathbf{e_x}+\omega_y \mathbf{e_y}+\mu\mathbf{e_z}$,容易证明$\lambda$满足下面的微分方程:$$\ddot{\lambda}-[\frac{(I_{yy}-I_{xx})(I_{zz}-I_{yy})}{I_{xx}I_{zz}}]\omega^2_y\lambda=0$$
该微分方程的通解为:$$\lambda=Ae^{kt}+Be^{-kt}$$
其中A,B为常数,且有:$$k=[\frac{(I_{yy}-I_{xx})(I_{zz}-I_{yy})}{I_{xx}I_{zz}}]^{1/2}\omega_y$$
这种情况下扰动角速度的幅值随着时间指数增长,转动稳定性被破坏。因此刚体绕Y轴旋转时对微小扰动不稳定。
结论:如果欧拉情况下刚体惯性主轴的三个转动惯量不相同,则绕最大和最小转动惯量对应的轴的旋转是稳定的,绕中间轴的旋转是不稳定的。如果其中有两个转动惯量相同,则可以证明刚体只有绕不同的那个轴旋转是稳定的。比如$I_{xx}=I_{yy}\neq I_{zz}$,则只有绕Z轴的转动是稳定的。
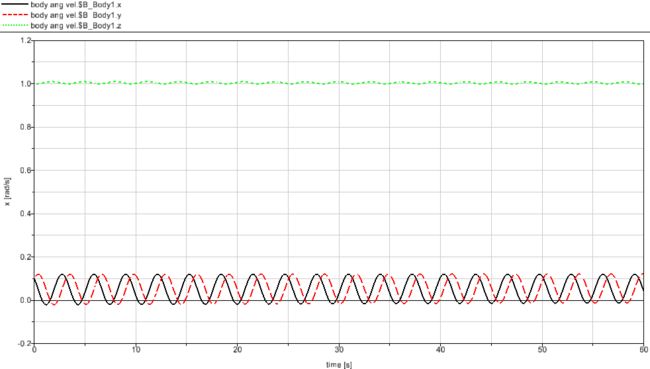
在SIMPACK动力学仿真软件中设置立方体的惯性张量为$I=diag(1,2,3)$,删除约束和重力并添加初始条件(Initial Conditions),让刚体主要绕Z轴旋转,角速度为1rad/s,X轴和Y轴扰动角速度设为0.1rad/s
在求解器设置中将积分时间改为60s,开始在线/离线仿真:
从结果的角速度曲线图可以看出在有微小扰动时刚体绕转动惯量最大的轴旋转是稳定的:
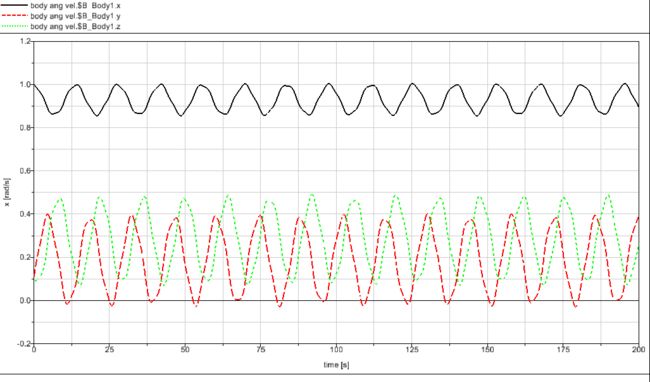
将初始角速度设为1,0.1,0.1,即主要绕X轴旋转,积分时间设为200s,仿真结果如下。可以看出在有微小扰动时刚体绕转动惯量最小的轴旋转是稳定的:
将初始角速度设为0.1,1,0.1,即主要绕Y轴旋转,积分时间设为200s,仿真结果如下。可以看出绕Y轴的转动不稳定:
参考:
Rotational Stability
关于刚体转动稳定性的研究
物理引擎中的刚体动力学
刚体质量分布与牛顿-欧拉方程
Gyroscope Physics
Gyroscopic forces in ODE
YouTube Gyroscopic forces in ODE
Game Physics-Numerical Integration
Free rotation of a rigid body animation
Integration Basics-How to integrate the equations of motion
Accurate and Efficient Simulation of Rigid Body Rotations
Stabilizing Gyroscopic Forces in Rigid Multibody Simulations