同余
在介绍补码之前先引入同余的概念,因为补码的原理利用了同余的性质。
同余是数论中最重要的基础概念之一,由德国数学家高斯在其1801年出版的«算术探索»中系统地进行了研究,书中所创造的同余符号"\(\equiv\)"也沿用至今。那么什么是同余呢?
【定义】给定正整数m,若有整数a、b,使得\(m|(a-b)\),则称a与b关于模m同余,记作\(a\equiv b(mod\,m)\).
例如对于m=8而言,1和9就是同余的,同理可知-7和1是同余的,9和17是同余的等等。由同余性质的等价关系可得到一个同余类:
\[\cdots\equiv -7\equiv 1 \equiv 9 \equiv 17 \equiv \cdots (mod\,8)\]
【推论】对于特定的正整数m,将有m个同余类.一般用\(0,1,\cdots ,m-1\)来唯一标识这m个同余类.
前面说补码利用了同余的性质,其实更准确的说法应该是补码利用了同余类之间的运算性质:
【性质一】若\(a\equiv b(mod\,m)\),\(x\equiv y(mod\,m)\),那么\(a+x\equiv b+y(mod\,m)\)
【性质二】若\(a\equiv b(mod\,m)\),\(x\equiv y(mod\,m)\),那么\(a\cdot x\equiv b\cdot y(mod\,m)\)
补码
在计算机世界中,任何数据都是一段二进制编码,是程序根据执行上下文来决定当前这段二进制编码具体表达了什么含义。
对于n位二进制编码而言,很自然地就可以表示0到\(2^n-1\)的数字。起初,我们可以很轻易地对这些数字进行加法或乘法运算,得到的结果是模\(2^n\)的余数。
为了让负数也能参与运算,补码定义最高位的bit为符号位,表示该位原本的值的相反数即\(-2^{n-1}\),为什么这样定义呢,因为这样得到的负数和原本的正数刚好相差了\(2\times 2^{n-1}\)。看到这里是不是很眼熟,那就是负数和对应的正数模\(2^n\)是同余的,也就是说补码没有用\(0,1,\cdots ,2^n-1\)来唯一标识同余类,而是用\(-2^{n-1},\cdots, 0,\cdots ,2^{n-1}-1\)来唯一标识同余类。这里演示当n=3时,各个二进制数所代表的数:
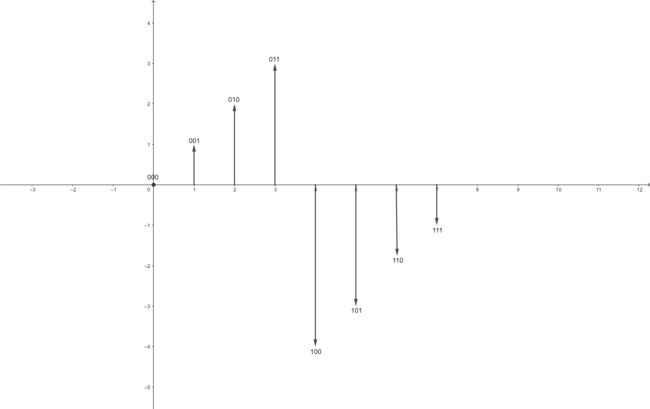
当要计算\(-4+1\)的时候,首先会将-4转换为模8的同余类4,再计算\(4+1\)模8的值得到5,再将5“解读”为对应的同余类-3。最终就得到了正确的结果。
用补码实现Int128
先实现了简单的加法,减法,乘法。除法麻烦一点,等以后有机会了再写吧。
//Int128.h
#pragma once
#include
#include //int64_t uint64_t
namespace rc {
class Int128 final {
public:
//提供默认构造函数,构造局部变量的时候为随机值
Int128() = default;
//没有explicit,允许整型隐式转换为Int128类型
template
Int128(IntegralType t_num) noexcept : m_high64(t_num < IntegralType(0) ? -1 : 0), m_low64(t_num) {}
//加法,相当于+=
Int128 &add(const Int128 &rhs) noexcept;
//减法,相当于-=
Int128 &sub(const Int128 &rhs) noexcept;
//乘法,相当于*=
Int128 &mul(const Int128 &rhs) noexcept;
//求补(求相反数)
Int128 &neg() noexcept;
//相等
bool equal(const Int128 &rhs) const noexcept;
//大于
bool greater(const Int128 &rhs) const noexcept;
//小于
bool lesser(const Int128 &rhs) const noexcept;
//大于等于
bool greaterOrEqual(const Int128 &rhs) const noexcept;
//小于等于
bool lesserOrEqual(const Int128 &rhs) const noexcept;
//取反(not作为函数名会报错)
Int128 &bitnot() noexcept;
//获取在内存中的16进制表示
std::string toHex() const;
private:
//计算64位整型的完整的128位积
static Int128 mul64(uint64_t x, uint64_t y) noexcept;
private:
int64_t m_high64;
uint64_t m_low64;
};
} //Int128.cpp
#include "Int128.h"
#include //ostringstream
#include //setw setfill
using namespace rc;
//加法,相当于+=
Int128 &Int128::add(const Int128 &rhs) noexcept {
//当低64位加法溢出将产生进位1
m_low64 += rhs.m_low64;
m_high64 += (rhs.m_high64 + (m_low64 < rhs.m_low64 ? 1 : 0));
//返回自身引用
return *this;
}
//减法,相当于-=
Int128 &Int128::sub(const Int128 &rhs) noexcept {
add(Int128(rhs).neg());
//返回自身引用
return *this;
}
//乘法,相当于*=
Int128 &Int128::mul(const Int128 &rhs) noexcept {
auto high64 = m_high64 * rhs.m_low64 + m_low64 * rhs.m_high64;
*this = mul64(m_low64, rhs.m_low64);
m_high64 += high64;
//返回自身引用
return *this;
}
//求补(求相反数)
Int128 &Int128::neg() noexcept {
//取反加1
bitnot();
add(1);
//返回自身引用
return *this;
}
//相等
bool Int128::equal(const Int128 &rhs) const noexcept {
return m_high64 == rhs.m_high64 && m_low64 == rhs.m_low64;
}
//大于
bool Int128::greater(const Int128 &rhs) const noexcept {
return m_high64 > rhs.m_high64 ? true : (m_high64 == rhs.m_high64 ? (m_low64 > rhs.m_low64 ? true : false) : false);
}
//小于
bool Int128::lesser(const Int128 &rhs) const noexcept {
return m_high64 < rhs.m_high64 ? true : (m_high64 == rhs.m_high64 ? (m_low64 < rhs.m_low64 ? true : false) : false);
}
//大于等于
bool Int128::greaterOrEqual(const Int128 &rhs) const noexcept {
return !lesser(rhs);
}
//小于等于
bool Int128::lesserOrEqual(const Int128 &rhs) const noexcept {
return !greater(rhs);
}
//取反(not作为函数名会报错)
Int128 &Int128::bitnot() noexcept {
m_high64 = ~m_high64;
m_low64 = ~m_low64;
//返回自身引用
return *this;
}
//获取在内存中的16进制表示
std::string Int128::toHex() const {
std::ostringstream os;
//setw设置域宽,使用一次就得设置一次
os << "0x"
<< std::hex << std::setfill('0')
<< std::setw(16) << m_high64
<< std::setw(16) << m_low64;
return os.str();
}
//计算64位整型的完整的128位积
Int128 Int128::mul64(uint64_t x, uint64_t y) noexcept {
//将x,y分解为32位整型
uint32_t xHigh32 = x >> 32;
uint32_t xLow32 = x;
uint32_t yHigh32 = y >> 32;
uint32_t yLow32 = y;
//计算各个位置的积
uint64_t low64 = static_cast(xLow32) * yLow32;
uint64_t mid64a = static_cast(xHigh32) * yLow32;
uint64_t mid64b = static_cast(xLow32) * yHigh32;
uint64_t high64 = static_cast(xHigh32) * yHigh32;
//计算最终的128位积
Int128 prod;
prod.m_low64 = low64 + (mid64a << 32);
prod.m_high64 = high64 + (mid64a >> 32) + (mid64b >> 32) + (prod.m_low64 < low64 ? 1 : 0);
//将最后剩下的mid64b的低32位数加进来
uint64_t mid32b = mid64b << 32;
prod.m_low64 += mid32b;
prod.m_high64 += (prod.m_low64 < mid32b ? 1 : 0);
return prod;
}