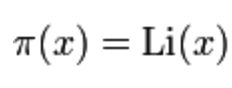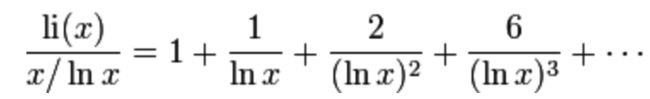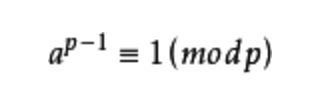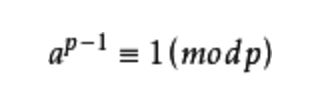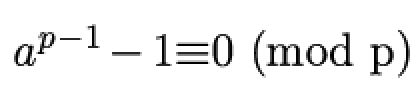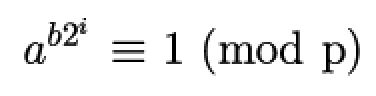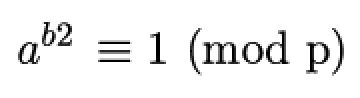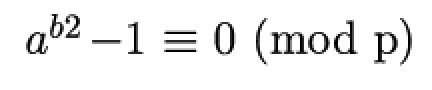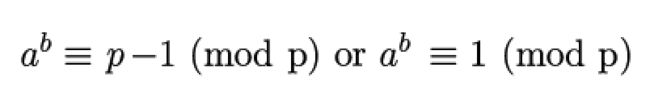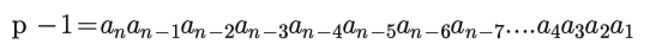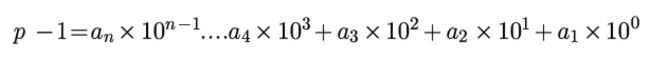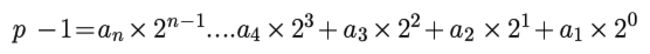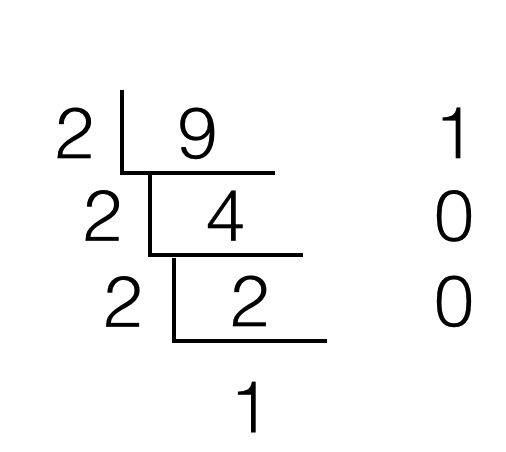2.白拿钱的游戏
为了激发大家的解题欲望和创造性,我们不妨想象这么一个场景。有一位有钱任性的还是个波霸的美女土豪找大家玩游戏,游戏规则如下:
土豪(波霸)给你若干张100元钱,其中有几张会是残破的。
比如这次给你2个亿,然后土豪会宣布这样的命令,找出2亿张100元以内最近的残破人民币。土豪这边有一张表,记录着其中第几张是残破的以作验证。最快找到的幸运儿会得到这200亿和土豪及其闺蜜的香吻。其他人没有奖励也没有惩罚。
看上去这样稳赚不赔的游戏,来玩的人自然是非常多,他们排起的长队跨过山,跨过大海,无惧狂风、不畏暴雨、烈日当做花朵在招手,在严冬中把自己比作傲骨的梅花。这条长龙首尾相连,靠人力证明了地球是圆的,外星人将这条队伍亲切地称为“地球的裤腰带”。
那是一个春天,你终于踏进了土豪家的大门,坐上了游戏桌。那么,什么样的策略能让你脱颖而出?
最笨的办法当然是从第一张开始往上数,灵光一点的办法是从最后一张往前数。
然而,你作为人群中最闪耀的那颗星,已经为这个游戏做了充分的背景调查,你了解到这位名位费殿的美女,小名叫素素。祖上是一位数学传奇——费马。
没错!真相只有一个——残破人民币的分布一定遵守素数分布规律。
这就是天才的直觉。
而且你听说了,但凡还能凑合上网的计算机不到0.3毫秒的时间就可以让你赢完土豪所有的积蓄(2^32张100元),1毫秒的时间可以吃下几亿个这样的土豪。
那么现在,所有的问题只剩下如何写这个程序了。
很容易发现素数分布肯定是越来越稀疏的。那么通过寻找这个稀疏的规律就可以发现素数密度的算法。
假设找到了范围,我们只需要能够判断一个数是不是素数的能力就行了。
世界就是这么充满着惊喜——这两种方法都已经有了
3.素数分布规律
在拿到分布规律之前,我们先可以自行猜想一番。如果中途你写出了这个规律,或者得到了较为精确的猜想,或许你可以查查祖上是否有个叫高斯的男子。
首先我们用笨办法,即试除法,找出一系列素数,我这里用删除线标注出来:
1
2 3
4
5
6
7
8 9 10
11
12
13
14 15 16
17
18 19 20...
把前n个自然数中的素数个数记做An,则A1=0,A2=1, A3=A4=2, A5=A6=3, A7=A8=A9=A10=4, A11=A12=5, A13=A14=A15=A16=6,A17=A18=19=A20=7...
依次类推,持续穷举下去。然后我们用An/n就可以得到素数的密度了
好啦。猜猜看吧
我当初连猜的机会也没有,因为我不小心看到了素数定理。
高斯是这样猜的:
An/n 渐进等于 1/ln n
是的,他猜且猜对了。关于这个定理的证明,受限篇幅,我换个时间再来细细品味它。
有了素数的密度,那么n内的素数个数很好得到了:
n/ln n
关于素数个数,人类还有个更好的估计(实际上还有更好的估计,但这里够了):
其中Li(x)是
我们需要展开它,方才容易写到程序里:
我们用 n/li(n) 就可以得到素数的密度估计值了
我们已经知道n/li(n)为素数密度,也就大致意味着每隔n/li(n)会出现一个素数。
那么我们不妨用n - n/li(n) 作为第一次猜测。
当然,这个数还需要一定的处理,因为它并不是自然数。最直接的思路,是四舍五入它,然后转换成整数。
如果n特别大,最好先对n/li(n)做整数处理。关于这一点,大家自己想想看为什么吧。
4.验证一个数是否为素数
现在我们已经得到了关于最大素数的第一个猜想值,现在我们需要知道如何验证一个数是不是素数。
莫非也有一个简单明了的公式?
是的,我们接近有这么一个公式。
这个定理描述如下:
如果p是任意一个不能整除整数a的素数,那么
(不知道为什么,每次输入“费马小定理”,我脑海中浮现的都是“麻辣小龙虾”)
许多人看到这个公式的第一反应便是,哎呀妈呀,太好了,这下判断素数太简单了。
只需求证p被a的p-1次方除时余数是不是等于1就好了,如果是,那么p是素数。
还有些朋友看到这个公式的第一反应是,这等于号(两横线)它哥(三横线)是什么玩意?这个mod又是什么东西?这些朋友请仔细看上面一句话,你就能明白这两个符号的意思了。三横线代表两边的数字除以p,余数是相等的,在这里余数都为1。
(关于费马小定理、欧拉函数请点击这里费马和欧拉)
还有些朋友性子比较急,已经开始拿起这个定理写素数判定程序了。他们一般这样写:
a取2,p为待证明素数。
一个个算下去,很快就来到了341这个“素数”。然而341=11*31。这是怎么回事?
这就好比,人都有嘴,但不能100%肯定有嘴的就是人一样,垃圾桶也有嘴。费马小定理只是说,p是任意一个不能整除整数a的素数,则有那样的性质。而不是说通过这个公式可以推断出p是素数,有可能并不是素数。
实际上存在这样一些合数,对于所有跟p互质的整数a,都满足费马小定理。这样的合数人类称它为开迈克尔数。
对于足够大的n,1-n内卡迈克尔数至少有:
n的2/7次方个
看来这种判定方法的错误率有点太高了。在题目范围内,即2的32次方内(4294967296),差不多有560多个开迈克尔数(实际上并不止这么一点)。
看来,我刚才骗人了,我说有这么一个公式,结果如此不精确,然并卵。
如果注意看的话,我刚才说到我们接近有这么一个公式。这句话背后的意思便是,人类有办法提高素数判定的精确度,这个提高的办法依然基于这个“不可靠”的费马小定理的逆命题。
5.提高素数判定的精确度
让我们把费马小定理再请出来围观一下:
要理解一个新事物,需要我们将它与原有的知识联系起来。那么我们一起看看,如何把费马小定理转化成我们熟悉的形式。
我们将1移到左边,得到:
这个形式看上去有没有熟悉一点?(关于为什么可以移动,大家可以自己推出来,我接下来的文章也会讲一讲)。保持这个模糊的熟悉感,我们继续。
令p-1=(2^i)*b (b为一奇数,因为p是一个不能整除整数a的素数,p肯定是一个奇数,因此p-1为一偶数):
同余符号两边持续开方,直到:
即:
这是我们熟悉的x的平方减1的形式
在这里,令c=a^b,同时我们保持c为小于p的整数。则c+1=p,或c-1=0。
所以有:
即:
这个式子说明,由费马小定理我可以得到这样的推论:
即对a的指数p-1不断提取2这个因子,直到和p-1是模p是同余的,如果与1同余,则继续提取2这个因子,直到2被提取完,最后与p-1或1是模p同余的
通过这个推论,我们可以对p进行更强的素数检测。当然,依然不能100%肯定通过这个检测的即为素数,我们只是把概率提高了一点。就像把有嘴的都是人上升到会抽烟的都是人(实际上还有会抽烟的动物),概率大大提高。
这种素数检测被称为 Miller-Rabin 测试。能通过Miller-Rabin测试的合数,我们称之为强伪素数。当a=2时,第一个强伪素数是2047。当同时检测a=2和a=3时,第一个强伪素数为1373653。我们可以发现,比单纯的费马检测要强有力的多。
6.算不出来的幂运算和求余
有了上面的基础,我们明白可以使用类似这样的代码来计算余数:
(modulo (expt a (- p 1)) p)
同时我们知道, Miller-Rabin 测试要经历多次类似这样的模运算,如果p很大的话,计算机可要吃不消喽。
看来我之前又骗大家了,我说一台勉强可以用的电脑都可以在1毫秒内得到结果。
最直接减少运算量的尝试就是减少Miller-Rabin测试的次数,也就是少用一点a。
好消息是,对于2^32这么小的数来说,a取2,3,61就够了。大家可以试一下如下运算:
(modulo (expt 61 4294967295) 4294967296)
大家的机器算了多久呢?时间就是金钱,虽然我的时间很便宜,但大家的青春是无价的。我先给大家一个心理预期,就是算这个余数的时间应该控制在0.02毫秒附近。
有人会说了,租个超级计算机来计算,反正能赢土豪的钱,接下来什么都有了。但是,现实当中,我们只是算个素数啊。清醒吧,少年。。
先不写了,容我把昨晚的剩饭热热。说实话,干这活真不挣钱。
7.很容易算的模运算
我们已经知道,对素数做测试最后一步一定是求余数,这是除法。除法本身就比较慢,何况这么大的数。之前的极大数冥运算也不是善茬。
为了找到解决问题的启发,我们回过头再看看之前的成果。
我们在为了得到Miller-Rabin算法的时候,一直在对同余符号两边开方,以得到“底层”的余数。那么反过来,我们可不可以通过对“底层”不断平方得到“上层”的结果?
如果可行,那真是毫无计算量啊。要知道,最“底层”的计算仅仅是一次方。
可是刚才,我们可是花了一点脑力才把指数下降到1,现在再升回去,岂不是在做无用功?
我们先从最基础的a的p-1次方开始一点点看:
因为两边是同一个数,所以两边不管模什么数,肯定是同余的,因此:
看上去好像没什么用,因为如果我们把每一个a都去求除以p的余数,因为a对于一个大数p来说,余数肯定还是a。最后的结果还是直接用a的p-1次方去做除法。哪怕是通过这条式子,我们联想到用尾递归去做乘法,减少内存开销,但最后依然避免不了大数除法带来的痛苦。
因此我们得继续变,这个变换为了减少计算量,需要尽量满足如下三个条件:
a.减少乘数的个数
b.乘数的每一除以p的余数与上一项有规律可寻,而且这个规律要足够简单,对于任意相邻两项都生效
c.尽量避免大数的除法
通过第二点,可以利用自然归纳法的思想,依次推到出所有乘数。这些乘数取得余数后相乘的结果再取余数得到最终结果。
那么,一个较大数的取余就转换成了计算第一个小数的余数,再依次计算接下来小数的余数(这个接下来的小数由之前一个余数得到)。听上去没有什么计算量了。
这个变换的结果会有如下的形式:
一上来就分析 b、c 这两个条件,似乎很难有突破。但是a条件,看上去不太可能实现啊。凭什么乘数就无端消失了。我们先不去想为什么a会没有,因为这个想通了,办法就唾手可得了。
我们先来看看,什么情况下可以省去一个a的?次方。
答案是 ? = 0
大家先别打我。 ?= 0。如果有这样的好事,那还算毛线啊。我的回答是,是的啊,很多时候,就是毛线都没计算,所以才那么快!
那么我们可以得到关于 ? 的一个式子:
现在问题已经被转换成p-1由一组0和其他数字的和构成了,那么这里的0是怎么得到的呢?
我们回到等式的左边,可以将p-1(一个n位数)构造为:
即:
这几乎就是我们想要的形式了,因为a是0-9的整数,也就是说我们已经构造出想要的0了。
但是,似乎我们给a的自由空间太大了一点0-9的选择太多了,而且它们作为a的指数还是太大了一点。我们应该对a的生存空间往最小了压缩,就像我们对待计算机一样,指给它0或1 。
于是我们得到:
我们再来看看我们想要达到的三个原则:
a.减少乘数的个数 (完成,出现很多1)
b.乘数的每一除以p的余数与上一项有规律可寻,而且这个规律要足够简单,对于任意相邻两项都生效 (完成,下一项为上一项系数不为0时的平方)
c.尽量避免大数的除法(每一次取余数时,值都很小。最终需要求余的数值为各项a不等于0时的余数的乘积)
我这里举个例子,刚才的
(modulo (expt 61 4294967295) 4294967296)
通过以上一系列运算,最终将会转换为求:
(modulo 3238827797 4294967296)
这个简直不用算,因为3238827797比4294967296小,因此余数为3238827797
这个算法叫Montgomery算法。或许我不应该告诉你?因为你靠自己已经推算出来了。
8.写出这个程序
8.1 求有多少个素数
根据li(n)的展开式,我们可以写出如下代码:
8.2 得到第一个猜想值
8.3 计算余数
刚才我们已经知道,要把指数转成2进制数。然后要搞清楚有多少位数,取完之后输出结果。这个结果是由所有系数为1的数的余数的乘积后取余数得到。其中相邻两项的余数构成平方关系。
听上去这个程序就不太好写。我们一步步来吧。
首先把指数转成2进制。我这里拿10进制数9举个例子:
9的二进制表达是1001
好了,我们已经拿到办法了。那就是对指数不停的除2取余数,取商数。直到商数为0为止,而这里的余数(0或者1)就是各项指数的系数。
除了商数和最终的待求余数的值,我们还要循环的是每一个前一项的余数。因为通过前一项的余数的平方我们直接得到了现在位置上的余数。
确认以上三点,写出程序就不难了:
其中a为底数,n为指数,即p-1,mod_n即为p(待确定“素数”)其实这里也可以只有两个变量,影响不大,看个人喜好了
我们首先求得第一项的余数 即a1,为接下来的循环做准备。n0为商数,作为停止程序运行的标志。n01为余数,作为判断是否将要将求得的值乘入at_last(最终要取余数的结果)当中。
8.4 Miller-Rabin测试
文章有些长,看到这里,大家可能已经有点淡忘这个测试的方法了。可以先去回顾一下,再继续看代码
还是先看看输入变量是什么,要迭代循环的量又是什么。
这个情况比sexy_mod要简单一些。输入就是底数a和待求素数p这两个变量。迭代的是指数p-1
首先要判断初始情况是否余数为1,然后开始循环。这其中要在余数为p-1时跳出程序直接返回#t。如果为1则继续循环直到指数为奇数,再对其求余看看是不是等于1或者p-1
如果不是以上的情况,要能直接跳出结果,即#f
想清楚了,代码也是很好写的:
8.5 利用测试的有效范围
刚才讲到以2为底的费马检测到341就不行了,以2,7,61为底对付这道题就就够了。如果想进一步减少运算量,也可以列出一些素数让待确认的数去除这些素数,如果除的尽就肯定不是素数了,也就没有必要进入miller-rabin测试了。
因此代码可以这样写:
8.6 向上取素数
直接猜就得到结果的可能性不是没有,但起码不是100%
它可能偏小,也可能偏大。如果比实际值要小,那么我们事先还不如不判断它是不是素数为好,减少一次计算。等到上面的值都不是素数,再看看猜的是不是,如果猜的也不是,就向下检测,向下检测比较简单,第一个得到的素数就是答案了。
在这里我们先看如何向上取素数。
首先我们要得到first_guess作为基准,其次拿n-1作为上限。因为n是否为素数的情况我们可以直接在主程序里判断。也就是说我们需要两个值的迭代,一个是现在的数值,另一个是现在的最大素数
那么,程序就像花朵的芬芳一样扑面而来了:
8.7 向下取素数
刚才已经讲了向下取的原则,代码也特别简单:
8.8 Max Prime
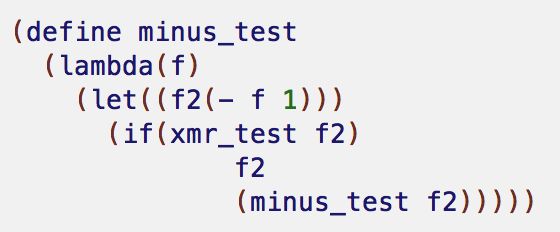
先判断输入是不是素数,是的话输出,不是的话下一步。在根据first_guess向上取素数,如果取完还是first_guess则看看first_guess是不是素数。这些都不是就调用minus_test。
8.9 测速
在这个max_prime程序中,其测试精确范围内程序运行时间稳定在在0.3毫秒左右。
如果想提高精确度,加几个底数就行了,也就是增加了几个毫秒级别的运算而已。
比如我选择2,3,5,7,11,13,17,19,23作为底数,可以准确检测3825123056546413051(380多亿亿)以下的数字。耗时1毫秒。
关于在多少范围内选取底数,大家可以参考维基百科Miller–Rabin primality test这个条目。
在racket里测速(runtime)的代码可以这样写,这里的单位是毫秒:
9 新的思索
这位美女不仅仅是土豪那么简单,她很快发现了你赢钱的秘密。于是——她要嫁给你。
然后你们一起躺在床上,你一边面露坚毅的眼神,一边缓缓道来,如何提升素数判定精度,如何推倒出冥的模运算,如何。。。
美女都挺尸了,噢不,听湿了
30秒后。。。
你已经做完了和美女在床上应该做的事情,现在,你又投入了新的思索。你顺手把电脑打开,将美女凉在一边。
我觉得作为一名码农,我们和农民有两点区别:
没有农民力气大
码农巴不得整天捧着电脑——这个他干活的工具。而农民不会整天抱着锄头跑