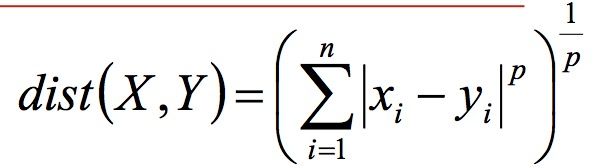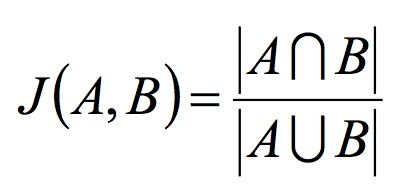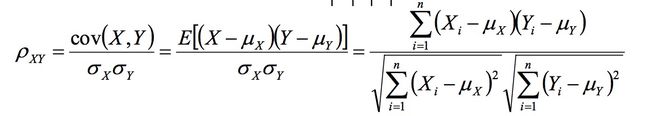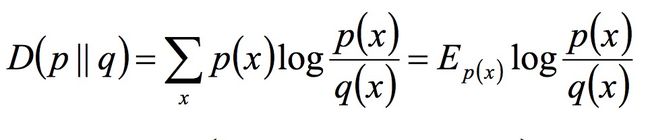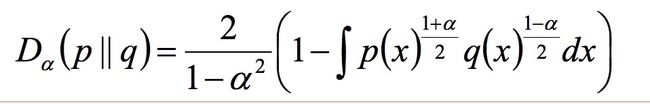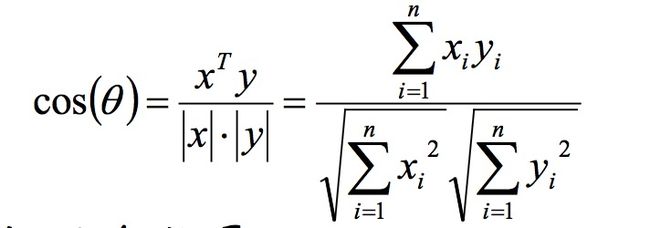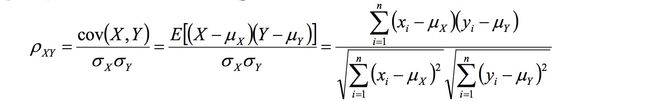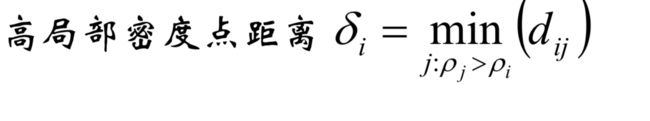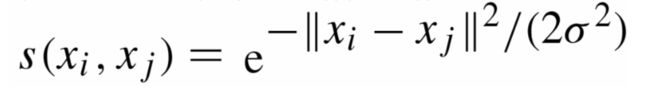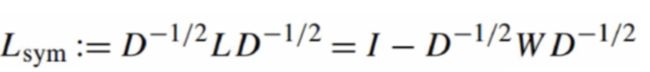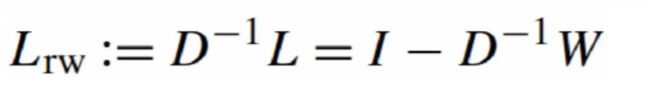聚类
- 聚类就是对大量未知标注的数据集,按数据 的内在相似性将数据集划分为多个类别,使 类别内的数据相似度较大而类别间的数据相 似度较小
- 无监督
如何计算相似度/距离
- 闵可夫斯基距离Minkowski/欧式距离 (针对坐标点):
- 杰卡德相似系数(Jaccard)(针对集合):
- 余弦相似度(cosine similarity)(针对向量):
- Pearson相似系数
- 相对熵(K-L距离)(K-L距离一般不对称):
- Hellinger距离
余弦相似度与Pearson相关系数的区别:
-
n维向量x和y的夹角记做θ,根据余弦定理,其余弦值为:
-
这两个向量的相关系数是:
相关系数即将x、y坐标向量各自平移到原点后的夹角余弦
- 这即解释了为何文档间求距离使用夹角余弦——因为这一物理
量表征了文档去均值化后的随机向量间相关系数。
聚类的基本思想:
给定一个有N个对象的数据集,构造数据的k 个簇,k≤n。满足下列条件:
- 每一个簇至少包含一个对象
- 每一个对象属于且仅属于一个簇
- 将满足上述条件的k个簇称作一个合理划分
基本思想:对于给定的类别数目k,首先给 出初始划分,通过迭代改变样本和簇的隶属 关系,使得每一次改进之后的划分方案都较 前一次好。
K-means算法:
输入:k, data[n];
- (1) 选择k个初始中心点,例如c[0]=data[0],…c[k-1]=data[k-1];
- (2) 对于data[0]….data[n], 分别与c[0]…c[k-1]比较,假定与c[i]差值最少,就标记为i;
- (3) 对于所有标记为i点,重新计算c[i]={ 所有标记为i的data[j]之和}/标记为i的个数;
- (4) 重复(2)(3),直到所有c[i]值的变化小于给定阈值。
K-means是对初值敏感的
簇近似为高斯分布的的时候,效果较好
迭代终止条件:
- 迭代次数
- 簇中心变化率
- 最小平方差
import numpy as np
def kmeans(X, k, maxIt):
'''
:param X: 数据集,数据集的最后一列表示标签值(或者组号)
:param k: k个分类
:param maxIt: 循环几次
:return:
'''
numPoints, numDim = X.shape
dataSet = np.zeros((numPoints, numDim + 1))
dataSet[:, :-1] = X
# Initialize centroids randomly
centroids = dataSet[np.random.randint(numPoints, size = k), :]
centroids = dataSet[0:2, :]
#Randomly assign labels to initial centorid
centroids[:, -1] = range(1, k +1)
# Initialize book keeping vars.
iterations = 0
oldCentroids = None
# Run the main k-means algorithm
while not shouldStop(oldCentroids, centroids, iterations, maxIt):
print("iteration: \n", iterations)
print ("dataSet: \n", dataSet)
print ("centroids: \n", centroids)
# Save old centroids for convergence test. Book keeping.
oldCentroids = np.copy(centroids)
iterations += 1
# Assign labels to each datapoint based on centroids
updateLabels(dataSet, centroids)
# Assign centroids based on datapoint labels
centroids = getCentroids(dataSet, k)
# We can get the labels too by calling getLabels(dataSet, centroids)
return dataSet
def shouldStop(oldCentroids,centroids,iterations,maxIt):
if iterations > maxIt:
return True
return np.array_equal(oldCentroids,centroids)
def updateLabels(dataset,centroids):
numPoints,numDim = dataset.shape
#算每一行的点离哪个中心点最近
for i in range(0,numPoints):
dataset[i,-1] = getLabelFromClosestCentroid(dataset[i,:-1],centroids)
def getLabelFromClosestCentroid(dataRow,centroids):
label = centroids[0,-1]
#numpy.linalg.norm传入任意两个向量,-为距离
minDist = np.linalg.norm(dataRow-centroids[0,:-1])
#找最小距离
for i in range(1,centroids.shape[0]):
dist = np.linalg.norm(dataRow-centroids[i,:-1])
if dist < minDist:
minDist = dist
label = centroids[i,-1]
print("minDist:"+str(minDist))
return label
def getCentroids(dataSet,k):
result = np.zeros((k,dataSet.shape[1]))
for i in range(1,k+1):
#所有求 标签值为i的值
oneCluster = dataSet[dataSet[:,-1]==i,:-1]
#axis =0 对行求平均值,axis=1 对列求平均值
result[i-1,:-1]=np.mean(oneCluster,axis=0)
#最后赋值标签
result[i-1,-1]=i
return result
x1 = np.array([1, 1])
x2 = np.array([2, 1])
x3 = np.array([4, 3])
x4 = np.array([5, 4])
testX = np.vstack((x1, x2, x3, x4))
result = kmeans(testX,2,10)
print("final result:\n"+str(result))
轮廓系数(Silhouette)
Silhouette系数是对聚类结果有效性的解释跟验证
计算样本i到同簇其他样本的平均距离为ai.ai越小,说明样本i越应该被聚类到该簇.称ai为样本i的簇内不相似度
计算样本i到其他某簇C1的所有样本的平均距离bil,称为样本i到簇c1的不相似度.bi越大,说明样本i越不属于其他簇
轮廓系数si:
$$S(i)=b(i)-a(i)/max{a(i),b(i)}$$
si接近1,说明样本i聚类合理,si接近-1,则说明样本i更应该分类到其他簇;若si 近似于0,说明样本i在两个簇的边界.
所有样本的si的均值为聚类结果的轮廓系数
密度聚类
DBSCAN算法
若干概念:
对象的ε-领域,给定对象在半径ε内的区域
核心对象:对于给定的数目m,如果一个对象的ε-领域至少包含m个对象,则称该对象为核心对象.
ε-领域内,而q是一个核心对象,我们说对象p从对象q出发是直接密度可达的.
密度可达:如果存在一个对象炼p1p2p3pn,如果p1=q,pn=p,则pi+1是从pi 关于ε 和m直接密度可达,
密度相连:如果对象集合D中存在一个对象o,使得对象p和q 是从o关于ε和m密度可达的,那么对象p和q是关于ε和m密 度相连的。
簇:一个基于密度的簇是最大的密度相连对象的集合。
噪声:不包含在任何簇中的对象称为噪声。
DBSCAN算法过程:
* 如果一个点p的ε-邻域包含多于m个对象,则创建一个p 作为核心对象的新簇;
* 寻找并合并核心对象直接密度可达的对象;
* 没有新点可以更新簇时,算法结束。
密度最大值聚类
局部密度:
dc是一个截断距离, ρi即到对象i的距离小于dc的对象的个 数。由于该算法只对ρi的相对值敏感, 所以对dc的选择是 稳健的,一种推荐做法是选择dc,使得平均每个点的邻 居数为所有点的1%-2%
高局部密度点距离:
简单的,就是:在密度高于对象i的所有对象中,到对象i最近 的距离,即高局部密度点距离.
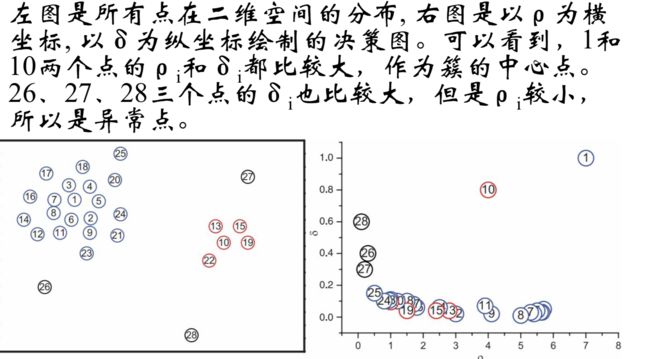
#####簇中心的识别:
那些有着比较大的局部密度ρi和很大的高密 距离δi的点被认为是 簇的中心;
高密距离δi较大但局部密度ρi较小的点是 异常点;
####密度最大值的分类过程:
###谱与谱矩阵
方阵作为线性算子,它所有的特征值的全体统 成为方阵的谱.
* 方阵的谱半径为最大的特征值
* 矩阵A的谱半径:(ATA)的最大特征值
#####谱分析过程:
给定一组数据x1,x2,...xn,记任意两个点之间 的相似度(“距离”的减函数)为sij=
相似度图G的建立:
* 全连接图:
高斯相似度函数:距离越大,相似度越小
* ε近邻图
小于ε的边裁掉
ε的选定:
图G的权值的均值
图G的最小生成树的最大边
* k近邻图(k-nearest neighbor graph)
直接选K个最近的
###拉普拉斯矩阵:
计算点之间的邻接相似度矩阵W
若两个点的相似度值越大,表示这两个点越相似;
同时,定义wij=0表示vi,vj两个点没有任何相似性(无穷远)
W的第i行元素的和为vi的度,形成了顶点度对角阵D
dii表示第i个点的度
除主对角线元素,D其他位置为0
未正则的拉普拉斯矩阵:$$L=D-W$$
随机游走拉普拉斯矩阵:
未正则拉普拉斯矩阵谱聚类算法:
输入:n个点{pi},簇的数目k
计算n×n的相似度矩阵W和度矩阵D;
计算拉普拉斯矩阵L=D-W;
计算L的前k个特征向量u1,u2,...,uk(从小到大);特征值的意义:降维处理
将k个列向量u1,u2,...,uk组成矩阵U,U∈Rn×k;
对于i=1,2,...,n,令yi∈Rk是U的第i行的向量;
使用k-means算法将点(yi)i=1,2,...,n聚类成簇 C1,C2,...Ck;
输出簇A1,A2,...Ak,其中,Ai={j|yj∈Ci}
hierarchical clustering 层次聚类
假如有N个待聚类的样本,步骤:
- (初始化)把每个样本归为一类,计算类之间的距离,(样本之间的相似度)
- 寻找各个类之间最近的两个类,把它们归为一类
- 重新计算新生产的这个类与各个旧类之间的相识度;
- 重复2,3,直到所有的样本点都归为一类.
距离的选择:
- SingleLinkage(nearest-neighbor)两个类中距离最近的两个点的距离作为两个类的距离.
- CompleteLinkage 正好相反.两个集合中距离最远的两个点的距离作为集合距离
- AverageLinkage 两个集合中点两两距离全部放在一起求均值
代码:
import numpy as np
class cluster_node(object):
def __init__(self,vec,left = None,right = None,distance = 0.0,id = None,count =1):
self.left = left
self.right = right
self.vec = vec
self.id = id
self.distance = distance
self.count = count
def L2dist(v1,v2):
return np.sqrt(np.sum((v1-v2)**2))
def L1dist(v1,v2):
return np.sum(np.abs(v1-v2))
def hcluster(features,distance = L2dist):
distances = {}
currentclustid = 1
clust = [cluster_node(np.array(features[i]),id=i) for i in range(len(features))]
##聚类过程
while len(clust) > 1:
lowestpair = (0,1)
closest = distance(clust[0].vec,clust[1].vec)
for i in range(len(clust)):
for j in range(i+1,len(clust)):
if (clust[i].id,clust[j].id) not in distances:
distances[(clust[i].id,clust[j].id)] = distance(clust[i].vec,clust[j].vec)
##找最短距离
d = distances[(clust[i].id,clust[j].id)]
if d < closest:
closest = d
lowestpair = (i,j)
##两个类的合并
mergevec = [(clust[lowestpair[0]].vec[i] + clust[lowestpair[1]].vec[i]) /2.0 \
for i in range(len(clust[0].vec))]
newcluster = cluster_node(np.array(mergevec),left=clust[lowestpair[0]],
right=clust[lowestpair[1]],distance=closest,id=currentclustid)
currentclustid = -1
del clust[lowestpair[0]]
del clust[lowestpair[1]]
clust.append(newcluster)
return clust[0]
def extract_clusters(clust,dist):
clusters = {}
if clust.distance < dist:
return [clust]
if clust.left != None:
cl = extract_clusters(clust.left,dist = dist)
if clust.right != None:
cr =extract_clusters(clust.right,dist = dist)
def get_cluster_elements(clust):
# return ids for elements in a cluster sub-tree
if clust.id>=0:
# positive id means that this is a leaf
return [clust.id]
else:
# check the right and left branches
cl = []
cr = []
if clust.left!=None:
cl = get_cluster_elements(clust.left)
if clust.right!=None:
cr = get_cluster_elements(clust.right)
return cl+cr
def printclust(clust, labels=None, n=0):
# indent to make a hierarchy layout
for i in range(n): print
(' '),
if clust.id < 0:
# negative id means that this is branch
print
('-')
else:
# positive id means that this is an endpoint
if labels == None:
print (clust.id)
else:
print(labels[clust.id])
# now print the right and left branches
if clust.left != None: printclust(clust.left, labels=labels, n=n + 1)
if clust.right != None: printclust(clust.right, labels=labels, n=n + 1)
def getheight(clust):
# Is this an endpoint? Then the height is just 1
if clust.left == None and clust.right == None: return 1
# Otherwise the height is the same of the heights of
# each branch
return getheight(clust.left) + getheight(clust.right)
def getdepth(clust):
# The distance of an endpoint is 0.0
if clust.left == None and clust.right == None: return 0
# The distance of a branch is the greater of its two sides
# plus its own distance
return max(getdepth(clust.left), getdepth(clust.right)) + clust.distance