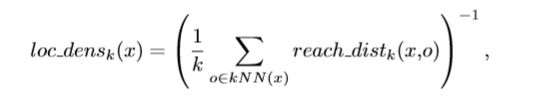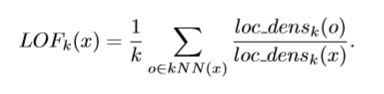教你用java实现时序数据异常检测(1)LOF-ICAD方法

数据的异常检测是一个难题, 面临许多挑战, 其中包括:

• 定义一个正常表现的范围是比较困难的, 异常值和正常值有时候边界并不是特别明显
• 某些恶意行为会伪装成正常值, 难以发现
• 大多数领域的正常行为只能在一段时间内有效, 对于未来的普适性并不是很高
• 对于异常的概念会由于应用的不同而不同
• 缺少带有标记的数据
• 数据的噪声可能有较大的影响

分析异常数据有多种方案, 包括:

• 基于分类的手段
• 基于最近邻算法
• 基于聚类
• 基于统计方法
• 基于信息理论
• 基于特征理论

我们这次着重介绍的是时序数据的异常检测, 我们来讨论讨论LOF方法, 并且给出相应的代码实现

1. LOF方法简介

该方法源自于论文Conformalized density- and distance-based anomaly detection in time-series data

LOF方法也就是Local Outlier Factor的缩写
首先我们需要引入一些符号:
k: 类似于KNN中的k, 代表第k个相邻的
dist(a,b): 表示a和b之间的距离, 可以是几何距离, 也可以是曼哈顿距离等

LOF方法使用对于第k个邻居的反向平均距离(Inverted average distance)来进行一个密度的测量, 我们记作loc_dens

密度的测量

同时我们给出其中的reach_dist

reach_dist

其中NN_k(x)是x的第k个近邻, 而reach_dist是为了当x和o彼此靠近的时候减少统计波动

我们计算出密度之后, 就要利用该密度和其他近邻的点进行比较, 进而我们就可以计算出异常程度的分数, 记为LOF, 按如下方法进行计算:

LOF

如果LOF越大则说明异常程度越高

2. LOF-ICAD方法

基于LOF方法, 论文给出了一种特征抽取的方法, 进一步提高了精度
这里直接给出算法的细节:

输入:

• 窗口长度L
• 合适的训练集合的大小T
• 修正集合的大小C
• 时间序列(x1, ... , x(T+C+L-1))
• 测试的值x(T+C+L)
• 密度测量NCM

输出(异常分数p, 从0到1):

步骤:

1. 将时间序列(x1, ... , x(T+C+L-1))映射到矩阵X, 其中矩阵X是L x (T+C)的矩阵
   举个例子, 比如对于时间序列(1, 2, 3, 4, 5, 6), T=2, C=2, L=3
   则生成X矩阵为
   1, 2, 3, 4
   2, 3, 4, 5
   3, 4, 5, 6
2. 将矩阵X划分成训练矩阵X(T)(L x T大小)以及修正矩阵X(C)(L x C大小)
   如上述例子, X(T)为:
   1, 2
   2, 3
   3, 4

3. 计算NCM值(α1, ..., αC)对于修正矩阵X(C)的每一行(应该会有L行)

   
   
   

   NCM
   
   

   具体的NCM值的计算也就是LOF的计算方式得到

4. 对序列最后的x(T+C+L-1)计算NCM值

   
   
   

   计算序列末尾的NCM

5. 计算异常程度分数p

   
   
   

   p的计算

如果p的分数特别高, 则异常程度相应地越高

3. Java实现

首先给出LOF算法的实现

package LOF;

import java.util.ArrayList;

/**
 * Local Outlier Factor
 *
 * @author mezereon E-mail:[email protected]
 * @since 18-4-12
 */
public class LOF {

  private int k;

  public LOF(int k) {
    this.k = k;
  }

  /**
   * 返回异常程度的分数， 越接近1则越异常
   *
   * @param knn 输入一个时序数据生成的旋转矩阵
   * @param x 输入测试的序列
   */
  public double getLOF(double[][] knn, double[] x) {
    double sum = 0;
    for (double[] o : knn) {
      sum += getLocDens(knn, o) / getLocDens(knn, x);
    }
    return sum / k;
  }

  /**
   * 获取local density
   *
   * @param knn 输入一个时序数据生成的旋转矩阵
   * @param x 输入测试的序列
   */
  public double getLocDens(double[][] knn, double[] x) {
    double[] nnk = findKthPoint(knn, x);

    double sum = 0;
    for (double[] o : knn) {
      sum += reachDist(o, x, nnk);
    }
    return sum / k;
  }

  /**
   * 找到第k个相似的序列
   *
   * @param knn 输入一个时序数据生成的旋转矩阵
   * @param x 输入测试的序列
   */
  public double[] findKthPoint(double[][] knn, double[] x) {

    ArrayList list = new ArrayList();
    for (int i = 0; i < knn.length; i++) {
      list.add(knn[i]);
    }
    int index = 0;
    double minDist = dist(knn[0], x);

    for (int i = 0; i < k; i++) {
      index = 0;
      minDist = dist((double[]) list.get(0), x);
      for (int j = 0; j < list.size(); j++) {
        if (minDist > dist((double[]) list.get(j), x)) {
          minDist = dist((double[]) list.get(j), x);
          index = j;
        }
      }
      if (i != k - 1) {
        list.remove(index);
      }
    }

    return (double[]) list.get(index);
  }

  /**
   * 返回与相似序列的距离比较之下的较大值
   *
   * @param o 输入序列
   * @param x 测试序列
   * @param nnk 第k相似的序列
   */
  public double reachDist(double[] o, double[] x, double[] nnk) {
    return Math.max(dist(o, x), dist(nnk, x));
  }

  /**
   * 返回序列之间的欧几里德距离
   *
   * @param nnk 第k相似的序列
   * @param x 测试序列
   */
  private double dist(double[] nnk, double[] x) {

    double sum = 0;
    for (int i = 0; i < nnk.length; i++) {
      sum += (nnk[i] - x[i]) * (nnk[i] - x[i]);
    }

    return Math.sqrt(sum);
  }

  public int getK() {
    return k;
  }

  public void setK(int k) {
    this.k = k;
  }
}

给出LOF-ICAD的实现

package LOF;

import Tool.DetectTool;
import Util.MatrixUtil;

/**
 * @author mezereon E-mail:[email protected]
 * @since 18-4-26
 */
public class LOFDetectTool implements DetectTool {

  private int T;// 时间序列用来训练的长度
  private int L;// 时间序列的所利用的窗口长度
  private int K = 1;//  LOF算法中的k值, 默认设置为1, 也就是取历史最相似的序列进行预测

  /**
   * LOF检测工具的构造方法
   *
   * @param T 时间序列用来训练的长度
   * @param L 时间序列的所利用的窗口长度
   */
  public LOFDetectTool(int T, int L) {
    this.T = T;
    this.L = L;
  }


  /**
   * 利用LOF进行时间序列分析
   * 打印最后一段窗口的异常分数, 越接近1则越异常
   */
  public void timeSeriesAnalyse(double[] series) {

    // 利用T和L, 以及时间序列生成测试矩阵
    double[][] mat = MatrixUtil.getMat(series, T, series.length - T - L + 1, L);

    //一个窗口大小的测试序列, 默认是原序列中最后窗口大小的序列
    double[] test = MatrixUtil.getTestSeries(series, series.length - L - 1, L);;

    double[][] matC = MatrixUtil.getMatC(mat, T, series.length - T - L + 1, L);
    double[][] matT = MatrixUtil.getMatT(mat, T, series.length - T - L + 1, L);

    LOF lof = new LOF(K);

    double[] ncmForC = new double[matC.length];

    for (int i = 0; i < matC.length; i++) {
      ncmForC[i] = lof.getLOF(matT, matC[i]);
    }

    double ncmForTest = lof.getLOF(matT, test);
    double count = 0;
    for (double x : ncmForC) {
      if (ncmForTest <= x) {
        count++;
      }
    }
    count /= matC.length;
    System.out.println("Anomaly Score is "+count);
  }
}

给出具体的Test类

public class LOFDetectToolTest {

  public double[] testData;
  @Before
  public void setUp() throws Exception {
    testData = FileTool.getData("data.json");
  }

  @Test
  public void timeSeriesAnalyse() throws Exception {
    LOFDetectTool lofDetectTool = new LOFDetectTool(200, 50);
    lofDetectTool.timeSeriesAnalyse(testData);
  }

}

4. 测试

测试序列1

对于上图序列计算得到的窗口异常分数为0.007092198
我们给它加一个峰值

测试序列2

得到的窗口异常分数为0.950354609

源码以及测试数据我已经放到github了
地址为https://github.com/MezereonXP/AnomalyDetectTool
其中包括自己编写的多种异常检测的工具类, 欢迎使用
希望大家多多Star, 有什么问题可以提issue给我, 或者发邮件到我的邮箱 [email protected]

下一篇, 将会介绍利用指数平滑进行异常检测的方法