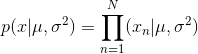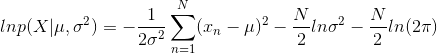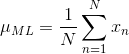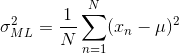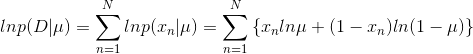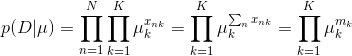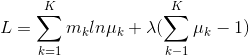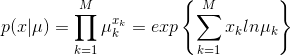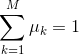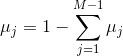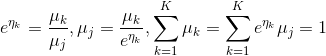「总结自经典机器学习教材《Pattern Recognition and Machine Learning》以及김동국教授的人工神经网络纯理论课程。在此感谢作者及教授的辛苦教学。本篇内容很多东西没有很明确地说明,仅限学习使用」
基本概要
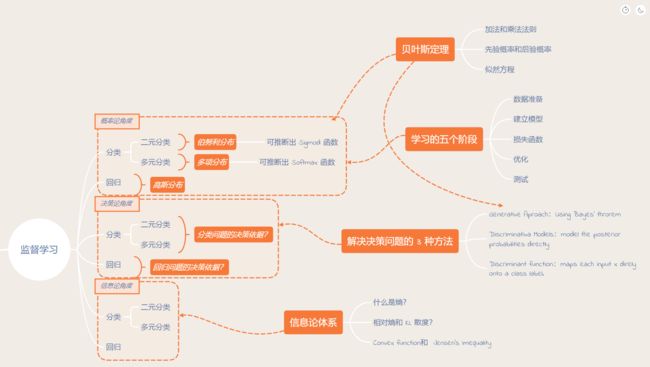
机器学习及模式识别领域主要由三大理论体系构成,分别是概率论(Probability Theory),决策论(Decision Theory)和信息论(Information Theory)。深度理解机器学习系列的文章主要从这三个理论来总结对机器学习相关知识的理解。对这些知识的深度理解也是为了能够看懂一些论文中的算法与推导,更深层次的深入机器学习领域。本篇文章从概率论开始入手。
机器学习领域的一个关键概念是不确定性(uncertainty)。然而概率论为不确定性的量化和操纵提供了框架,并形成了机器学习的核心基础之一。当与后面讨论的决策论相结合时,其可以根据一些可获得的信息做出最佳预测,即使这些信息可能并不完整。
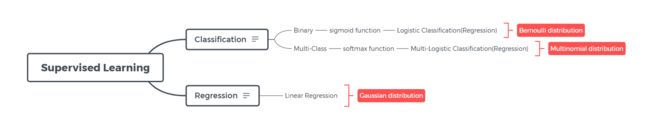
机器学习包括监督学习,非监督学习和强化学习这 3 类。监督学习分为分类(classification)和回归(regression)这两部分应用。分类和回归的最大区别是分类是离散的,而回归是连续的。分类又包括二元分类和多元分类。与二元分类有关的是伯努利分布(Bernoulli distribution);与多元分类有关的是多项分布(Multinomial distribution)。而与回归有关的是高斯分布(Gaussian distribution)。后面的内容主要是从概率的角度说明分类和回归模型与这些概率分布之间的关系。
概率中的基本法则
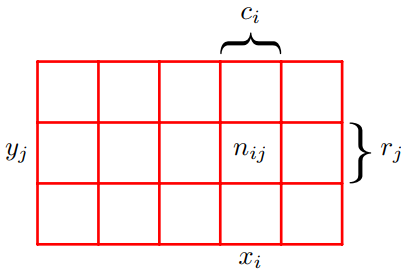
为了讲清楚概率中基本的两个法则,可以先考虑两个随机变量 X 和 Y 的概率。其中随机变量 Xi 的取值为 {xi},i = 1,2,3...M;随机变量 Yj 的取值为 {yj},j = 1,2,3...L。假设 M = 5,L = 3。如果我们考虑这些变量的实例的总数为 N,那么我们用 nij 表示 X = xi 和 Y = yj 时的实例,nij 是数组的相应单元中的点。i 列中对应于 X = xi 的点由 ci 表示,并且 j 行中对应于 Y = yj 的点数由 rj 表示。具体如下图所示:
接下来我们可以这样考虑:X 可以取 {xi},i = 1,2,3...M 中的任意值;Y 可以取 {yj},j = 1,2,3...L 中的任意值。总共有 N 次试验,对 X 和 Y 两个样本进行随机抽样。当 X = xi ,Y = yj 时,试验的次数为 nij 。另外,让 X 取 xi 的试验次数(无论如何 Y 为何值)用 ci 表示; Y 取 yj 的试验次数(无论如何 X 为何值)用 rj 表示。
当 X 取 xi ,Y 取 yj 时,其概率被记为 p( X = xi ,Y = yj ),该概率称为 X,Y 的联合概率(joint probability)。它是由落在单元格 i,j 中的点的总和除以所有点的总和得出的。即:
同样,不管 Y 的取值,X 的概率为落在单元格一列的点的总和除以所有点的总和,如下所示:
因为在 i 列中,实例的总数就是该列中每个单元格表示的实例的总和。有 ci = ∑jnij,所以有:
这个就是概率的加法法则。有时候 p( X=xi )也被称为边缘概率(merginal probability)。
如果在有了 X = xi 的情况下,计算 Y = yj 的概率被称为条件概率(condition probability)。通过找到落在单元格 i,j 中的点除以落在 i 列中的点的总数来计算:
结合以上的公式,可以推导出下面的公式,这就是概率中的乘法法则:
总结:给定两个随机变量 X 和 Y,定义 P(X),P(Y) 分别是随机变量 X 的概率和随机变量 Y 的概率;P(X,Y) 是 X 和 Y 的联合概率(joint probability);P(X) 是边缘概率(merginal probability),表示 X 出现的概率;P(Y|X) 是在给定 X 的情况下 Y 的概率;P(X|Y) 是在给定 Y 的情况下 X 的概率。
- 加法法则:
- 乘法法则:
贝叶斯定理
贝叶斯定理是结合了加法法则和乘法法则,并根据 P(X,Y) = P(Y,X) 的对称性,推导出以下公式:
贝叶斯定理在模式识别和机器学习中扮演着一个很重要的角色。贝叶斯思想也贯穿于《Pattern Recognition and Machine Learning》这本书的始终,因此搞懂它很有必要。
举一个简单的例子来理解。假设有红色和蓝色两种颜色的盒子各一个,在红盒子中有 2 只苹果和 6 只橘子;在蓝盒子中有 3 只苹果和 1 个橘子。已知,会有 40% 的几率选择红盒子;60% 的几率选择蓝盒子。此时,已经取出一只橘子,问它从红盒子中取出的概率为多少?
首先,做一些定义。将盒子记为 B ,B = r 表示红盒子,B = b 表示蓝盒子;将水果记为 F ,F = o 表示橘子,F = a 表示苹果。p(B)表示选择盒子的概率,我们可以知道选择红盒子的概率为 p(B = r)= 4/10;选择蓝盒子的概率为 p(B = b) = 6/10。
接着,计算取一只水果是橘子的概率:
根据贝叶斯定理,要计算一只橘子从红盒子中取出的概率 p(B = r|F = o),还需要知道从红盒子中取出一只橘子的概率 p(F = o|B = r),其可以由已知条件直接计算出来为 3/4。
最后根据贝叶斯定理的公式计算:
下面就可以对贝叶斯做一个简单的解释。将概率 p(B) 称之为先验概率(prior probability),因为其是我们在观察水果特性之前就已经获得的概率。将 p(B|F) 称之为后验概率(posterior probability),因为它是概率在获得概率 p(F) 之后得到的概率。一旦我们被告知水果是橘子,我们就可以使用贝叶斯定理来计算概率 p(B|F) 。一开始,直观地看,选择蓝盒子的先验概率是 60% ,比选择红盒子的概率要大。所以我们可能会更多的选择蓝盒子。然而计算结果显示取出一只橘子,其来自红盒子的后验概率为 2/3,比来自蓝盒子的概率要大。所以,观察到水果是橘子的话将会提供很重要的证据来支持其来自红盒子。事实上,证据足够有力 - 超过了先前的概率的话,使结果更有可能选择红盒子而不是蓝盒子。这就是贝叶斯定理的思想,它能够告知我们如何利用新证据来修改已有的看法。
概率密度
上面举的水果的例子,样本变量是离散的。接下来要讨论连续变量的概率。仅限于非正式的讨论。 如果是实数变量 x 落入区间 (x,x +δx) 的概率被定义为 p(x)δx (δx→0),则 p(x) 被称为 x 的概率密度(probability density)。然后,x 位于区间(a,b)中的概率可以表示为:
因为概率是非负的,并且因为 x 位于实轴的某处,所以概率密度 p(x) 必须满足下面两个条件:
对于无限的情况,则有以下条件:
对于概率密度的情况,概率的加法法则,乘法法则以及贝叶斯定理一样适用:
贝叶斯概率
上面我们已经了解了频率随机的,可重复事件的概率。其也被称为经典的或者基于频率的角度来解释概率。现在我们转向更普遍的贝叶斯视角,它能够量化不确定性。
将频率概率应用于随机变量来观察其随机值似乎是合理的。但是,我们希望解决和量化围绕着选择模型参数 w 的不确定性。从贝叶斯的角度来看,我们可以使用概率论的机制来描述模型参数中的不确定性,例如 w,或者选择模型本身。
这里,针对机器学习的某一模型做出一些定义。在观察数据之前,我们以先验概率的形式假设关于参数 w 的概率分布 p(w)。观察到的数据 D = {t1,t2,,...tN} 的影响通过条件概率被表示为 p(D|w) 。贝叶斯定理公式,可以由如下公式表达:
然后我们可以在公式中用观察到的数据 D 和后验概率 p(w|D) ,评估 w 中的不确定性。在公式的右边 p(D|w) 用来评估观察到的数据集 D 以及可以被看成是关于参数向量 w 的函数,此函数被称为似然方程(likelihood function)。它表示对于参数向量 w 的不同设置,观测到的数据集的可能性有多大。注意,似然估计不是关于 w 的概率分布,其对 w 的积分不一定等于 1 。
有了对似然估计的定义后,可以将贝叶斯定理概括成如下几个单词:
即:后验概率正比于似然估计和先验概率的乘积。对于似然方程的具体内容会在后面总结。
高斯分布
这里针对连续变量,总结一下关于高斯分布的一些内容。对于单个实数变量 x 来说,它的高斯分布公式如下所示:
其中 μ 表示均值(mean),σ 表示方差(variance),β = 1/σ2 表示精度(precision)。
对于 n 维实数变量来说,其高斯分布公式如下:
其中 n 维向量 μ 表示均值(mean),Σ 表示协方差(covariance)。
高斯分布被用于机器学习中的回归模型。后面会具体说明。
回归问题与高斯分布之间的关系
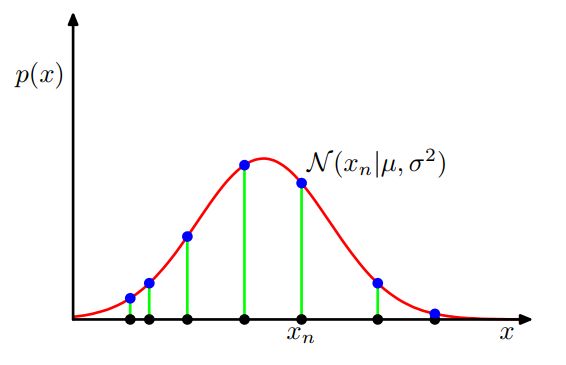
现在假设我们观测到一系列 X 的数据集: X =(x1,x21,x3...x1,xN)T,表示标量 X 的 N 个观测值。并绘制一个高斯分布,如下图所示,该高斯分布的均值 μ 和方差 σ2 是未知的。我们想要从数据集中确定这些参数。我们将独立于同一分布绘制的数据点称为独立恒等分布(independent and identically distributed),通常缩写为i.i.d。从开头概率的基本法则介绍中,我们已经知道,两个独立事件的联合概率由每个事件的边际概率的乘积给出。因为我们的数据 X 是 i.i.d。所以我们可以给出给定 μ 和 σ2 时,数据集 X 的概率为:
该公式也被称为高斯的似然方程。
使用观测到的数据集确定概率分布中的参数的一个常见标准是找到参数值使得似然函数最大化。这看起来貌似是一个很奇怪的标准,因为,从我们之前对概率论的讨论中,在给定数据的情况下,最大化参数的概率似乎更自然,而不是在给定参数的情况下最大化数据。然而实际上,这两个标准是相近的。
接下来我们要将似然方程最大化来求得高斯分布中均值 μ 和方差 σ2 的取值。在实际应用中,将似然函数的对数最大化更为方便。因为对数是其参数的单调递增函数,函数的对数的最大化就等于函数本身的最大化。取对数不仅简化了后续的数学分析,而且在数值计算上也有帮助,因为大量的小概率的乘积很容易使计算机的数值精度下降,而这可以通过计算对数概率的总和来解决的。对数似然方程可以表示为如下形式:
对上面式子分别求解偏分为 0 的情况,可以分别得出 μ 和 σ2 的值,如下所示:
分类问题与概率分布之间的关系
在机器学习的监督学习中,分类问题与回归问题的区别是:分类问题的数据是通常是离散的随机变量,为回归问题的数据是连续的随机变量。这篇文章讲讲,分类问题与概率分布之间的关系,以及是如何推导出 Sigmoid 函数和 Softmax 函数的,还有分类问题的其他一些底层知识。
二元分类及其概率分布
常见的二元变量是这样的:x ∈ {0,1} 。举一个具体的例子,比如识别一张图片中是不是猫的例子。假设 1 表示是,0 表示不是。我们可以这样定义,结果是猫的概率为:p( x=1| μ) = μ, 其中 μ 是参数,其范围为: 0 <= μ <= 1。所以结果为不是猫的概率为:p( x=0| μ) = 1 - μ 。总体可以写成这样:Bern( x | μ ) = μx(1 - μ) 1-x。可以发现该式子是伯努利分布(Bernoulli distribution),又称两点分布或者 0-1 分布,是一个离散型概率分布。
现在假设我们有一个数据集 D = {x1,…,xN}, 其为 x 的观测值。我们可以构造一个关于参数 μ 的似然函数,假设观测是独立于 p(x|µ) 的,所以有如下式子:
为了计算出识别结果为猫和不是猫的概率,我们必须得求解出参数 μ 。为了使问题变得简单,对上面的似然方程进行 log 操作,如下所示:
当 lnp(D|μ) 的导数为 0 时,我们可以获得最大的似然估计(其也是求得最佳参数的方法之一):
如果知道数据集中结果为 1 的总数量 m 的话,结果可以写成这样:
多元分类及其概率分布
多元分类就是识别一张图片,分辨其属于猫,狗,猪,鸭,鱼等多个类别中的哪个类别。常见的多元分布的变量是这样的:x ∈ {1,2, ... , k }。但是在机器学习中常用 one-hot 向量表示它们,可以参考这篇文章: 数据预处理-对类别数据的处理方法 。
使用 one-hot 编码处理数据后,假设 x3 = 1,其 one-hot 向量为:x = (0,0,1,0,0...)T。即可以写成这样的表达:∑k xk =1。如果通过参数 μ 来表示关于 xk 的概率,可以写成如下式子:
其中 μ = (μ1,μ2,... μk)T,因为 μ 表示概率,所以其范围限制为:μ1 >= 0,∑μk =1。可以发现这是多项分布的公式。
现在假设我们有一个数据集 D = {x1,…,xN}, 其为 x 的观测值。我们可以构造一个关于参数 μ 的似然函数,有如下式子:
为了求解出参数 μ ,这时候需要引入拉格朗日乘数法。因为这里 μ 的范围是有限制的,不能用之前的方法求解。
补充:拉格朗日乘数(Lagrange Multiplier)
在数学中的最优化问题中,拉格朗日乘数法(以数学家约瑟夫·拉格朗日命名)是一种寻找多元函数在其变量受到一个或多个条件的约束时的极值的方法。这种方法可以将一个有n个变量与k个约束条件的最优化问题转换为一个解有n + k个变量的方程组的解的问题。这种方法中引入了一个或一组新的未知数,即拉格朗日乘数,又称拉格朗日乘子,或拉氏乘子,它们是在转换后的方程,即约束方程中作为梯度(gradient)的线性组合中各个向量的系数。 -- 来自维基百科
对于一个二元函数,如果没有限制条件的话,通常直接使用求导的方法来求得极值。如果参数变量有限制条件的话,就需要用到拉格朗日乘数的方法来求解。比如,要求 f(x,y) 在 g(x,y) = c 时的最大值,我们可以引入新变量拉格朗日乘数 λ,这时我们只需要求解下列拉格朗日函数的极值:
下面举一个简单的例子来说明。假设 f(x,y) = x2 + y2 ,其中 g(x,y) = y + x = 1。要求求出 f(x,y) 的极值。
根据已知条件,可以得出拉格朗日函数为:L = x2 + y2 + λ(x + y -1)。为了求出极值,先计算 L 分别对于 x 和 y 的偏导数,分别如下方:∂L/∂x = 2x + λ,∂L/∂y = 2y + λ。又因为 x + y = 1,即 -λ = 1,所以求出 λ = -1。因而求得:x = -1/2,y= -1/2 。将 x,y 的值代回到拉格朗日函数中即可求得极值。
回到多元分类的问题中,求解 log - 似然方程极值对应的参数变量 μ 的值。因为 μ 是有范围限制的,所以需要使用拉格朗日乘数法。即化简可以得到:
对其求偏导数可得到:∂L/∂μk = mk / μk + λ = 0 ,即:μk = - mk / λ 。又因为 mk = ∑k xnk = N ,可以求得 λ = -N,所以 μML.k = mk / N
指数族分布
指数族分布(Exponential family Distribution )是在给定参数 η 后,基于 x 的分布。定义式如下所示:
其中 x 可以为标量也可以为向量,可以是离散的,也可以是连续的。η 表示分布的自然参数。u(x) 是关于 x 的函数。函数 g(η) 可以解释为确保分布标准化的系数,它满足下面式子:
Sigmoid 函数的推导
再次回到伯努利分布的式子:Bern( x | μ ) = μx(1 - μ) 1-x,将其 log 化后,再进行转换可以得到:
观察发现其实符合指数族分布的特征的。因此,可以得出 η = ln(u/1-u),再将其转换回指数函数的类型,可以得到:eη = u/1-u。最后可以得出求解 u 的式子:u = 1/(1+e-η), 其范围也符合上面定义的 0 <= μ <= 1 。这个式子是不是很熟悉,这个就是著名的 Sigmoid 函数。
用 σ(η) 来表示,即为 σ(η) = 1/(1+e-η)。所以伯努利分布也可以表示成这样:
根据公式也能发现这样的特性:1 − σ(η) = σ(−η),所以指数族分布的相关函数可以表示成:μ(x) = x ;h(x) = 1;g(η) = σ(−η)。
Softmax 函数的推导
同理,将多项分布的式子,将其 log 化后,再进行转换可以得到:
观察发现其也是指数族分布。因此,可以得到:η = lnμk,μ(x) = x ;h(x) = 1;g(η) = 1。p(x|μ)= exp(nTx) 。
需要注意的是参数 μ 并不独立,其受到下方式子的约束:
只需要算出前 M-1 个参数,就可以计算出全部的参数了。因此,有:
现在可以确定:
此时令[1] μj 如下所示,已知 M 个参数的总概率为 1 和 M-1 参数的概率,所以第 M 个参数的概率就很容易求得:
可以得到:
此时可以得到:
将 μj = μk / eηk,代入上式,可得:
为了区别分母的累加,将下标 k 改为 j,既有:
以上就是 Softmax 函数的推导过程了。
参考及扩展
[1]. 数学之美番外篇:平凡而又神奇的贝叶斯方法
[2]. When Bayes, Ockham, and Shannon come together to define machine learning
[3]. A Gentle Introduction to Maximum Likelihood Estimation
[4]. softmax函数