小橙书阅读指南（五）——归并排序的两种实现

算法描述：将两个较小的有序数组合并成为一个较大的有序数组是比较容易的事情。我们只需要按照相同的顺序依次比较最左侧的元素，然后交替的放进新数组即可。这就是自顶向下的归并排序的实现思路。与之前的算法不同的是，归并排序需要使用额外的存储空间，用空间换时间的做法也是在排序算法中经常需要做的选择。

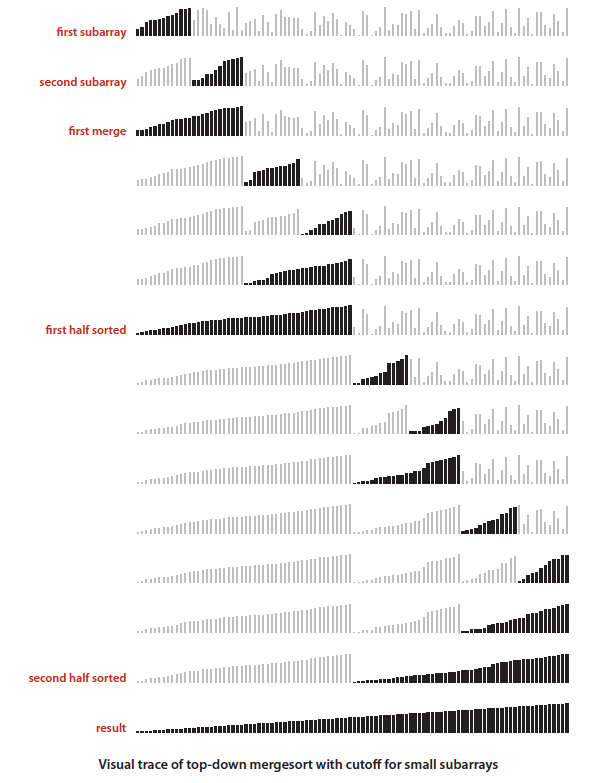
算法图示：

算法解释：把一个较大的数组不断划分为较小的两个数组，直到无法再切分之后再做逆向合并，并再合并的过程中调整顺序。归并算法的难点是如何尽可能的减少额外存储空间的使用。

Java代码示例：

package algorithms.sorting;

import algorithms.Sortable;
import algorithms.common.ArraysGenerator;

import java.util.Arrays;

public class Merge implements Sortable {
    private Integer[] aux;

    @Override
    public void sort(Integer[] array) {
        aux = new Integer[array.length];
        sort(array, 0, array.length - 1);
    }

    private void sort(Integer[] array, int lo, int hi) {
        // 递归结束条件
        if (hi <= lo) {
            return;
        }
        int mid = lo + (hi - lo) / 2;
        sort(array, lo, mid);
        sort(array, mid + 1, hi);
        merge(array, lo, mid, hi);
    }

    private void merge(Integer[] array, int lo, int mid, int hi) {
        int i = lo;
        int j = mid + 1;
        // aux数组作为成员变量，长度与array相同。重复使用，以节约存储空间。
        for (int index = lo; index <= hi; ++index) {
            aux[index] = array[index];
        }

        for (int index = lo; index <= hi; ++index) {
            // 如果低位数组用完 则 将高位数组依次复制
            if (i > mid) {
                array[index] = aux[j++];
            }
            // 如果高位数组用完 则 将低位数组依次复制
            else if (j > hi) {
                array[index] = aux[i++];
            }
            // 如果高位数组最左侧元素 小于 低位数组最左侧元素 则 将高位数组最左侧元素复制
            else if (aux[j] < aux[i]) {
                array[index] = aux[j++];
            }
            // 如果低位数组最左侧元素 小于或等于 高位数组最左侧元素 则 将低位数组最左侧元素复制
            else {
                array[index] = aux[i++];
            }
        }
    }

    public static void main(String[] args) {
        Integer[] array = ArraysGenerator.generate(10, 0, 100);
        Merge merge = new Merge();
        merge.sort(array);

        System.out.println(Arrays.toString(array));
    }
}

Qt/C++代码示例：

#include "merge.h"

Merge::Merge()
{

}

Merge::~Merge()
{
    if (aux) {
        delete aux;
    }
}

void Merge::sort(int *arr, int len)
{
    if (aux) {
        delete aux;
    }
    aux = new int[len];
    sort(arr, 0, len - 1);
}

void Merge::sort(int *arr, int lo, int hi)
{
    if (hi <= lo) {
        return;
    }
    int mid = lo + (hi - lo) / 2;
    sort(arr, lo, mid);
    sort(arr, mid + 1, hi);
    merge(arr, lo, mid, hi);
}

void Merge::merge(int *arr, int lo, int mid, int hi)
{
    int loIndex = lo; // 低位数组起始坐标
    int hiIndex = mid + 1; // 高位数组其实坐标
    // 复制数组
    for (int i = lo; i <= hi; ++i) {
        aux[i] = arr[i];
    }

    for (int i = lo; i <= hi; ++i) {
        if (loIndex > mid) {
            arr[i] = aux[hiIndex++];
        }
        else if (hiIndex > hi) {
            arr[i] = aux[loIndex++];
        }
        else if (aux[hiIndex] < aux[loIndex]) {
            arr[i] = aux[hiIndex++];
        }
        else if (aux[loIndex] <= aux[hiIndex]) {
            arr[i] = aux[loIndex++];
        }
    }
}

自顶向下的归并排序算法的动态图示：

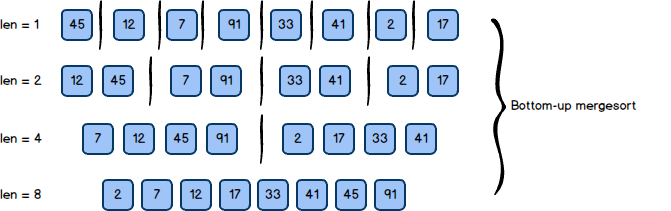
自底向上的归并排序算法的动态图示：

算法解释：首先以1为步长调整array[i]和array[i+1]，接着是array[2*i]和array[2*i+1]直到完成整个数组的第一轮调整。接下来以2为步长调整array[i]，array[i+1]和array[2*i]，array[2*i+1]直到完成整个数组的第二轮调整。

Java代码示例：

package algorithms.sorting;

import algorithms.Sortable;
import algorithms.common.ArraysGenerator;

public class MergeBU implements Sortable {
    private Integer[] aux;

    @Override
    public void sort(Integer[] array) {
        aux = new Integer[array.length];
        for (int len = 1; len < array.length; len = 2 * len) { // 每次选取的子数组的长度
            for (int lo = 0; lo < array.length - len; lo += 2 * len) {
                merge(array, lo, lo + len - 1, Math.min(lo + (2 * len) - 1, array.length - 1));
            }
        }
    }

    private void merge(Integer[] array, int lo, int mid, int hi) {
        int loIdx = lo;
        int hiIdx = mid + 1;
        for (int i = lo; i <= hi; ++i) {
            aux[i] = array[i];
        }
        for (int i = lo; i <= hi; ++i) {
            if (loIdx > mid) {
                array[i] = aux[hiIdx++];
            } else if (hiIdx > hi) {
                array[i] = aux[loIdx++];
            } else if (aux[hiIdx] < aux[loIdx]) {
                array[i] = aux[hiIdx++];
            } else {
                array[i] = aux[loIdx++];
            }
        }
    }

    public static void main(String[] args) {
        Integer[] array = ArraysGenerator.generate(1000, 0, 9999);
        MergeBU mergeBU = new MergeBU();

        mergeBU.sort(array);
        System.out.println(ArraysGenerator.isSort(array, "asc"));
    }
}

Qt/C++代码示例（略）

有关算法效率的解释很多，不过按照我自己的测试归并算法是目前侠侣最高的排序算法。

相关链接：

Algorithms for Java

Algorithms for Qt