面试算法——快速排序

1.概念

快速排序，听这个名字就能想到它排序速度比较快方法，是一种分治思想，现在各种语言中自带的排序库很多使用的都是快速排序。

空间复杂度

快速排序是一种原地排序，只需要一个很小的栈作为辅助空间，空间复杂度为O(log₂n)，所以适合在数据集比较大的时候使用。

时间复杂度

时间复杂度比较复杂，最好的情况是O(n)，最差的情况是O(n²)，所以平时说的O(nlogn)，为其平均时间复杂度。

2.基本思想

随机找出一个数，可以随机取，也可以取固定位置，一般是取第一个或最后一个称为基准，然后就是比基准小的在左边，比基准大的放到右边，如何放做，就是和基准进行交换，这样交换完左边都是比基准小的，右边都是比较基准大的，这样就将一个数组分成了两个子数组，然后再按照同样的方法把子数组再分成更小的子数组，直到不能分解为止。

3.举例说明

下面这段是我从网上摘抄的，排序过程各种博客文章例子也比较多了。

 

假设我们现在对“6  1  2 7  9  3  4  5 10  8”这个10个数进行排序。首先在这个序列中随便找一个数作为基准数（不要被这个名词吓到了，就是一个用来参照的数，待会你就知道它用来做啥的了）。为了方便，就让第一个数6作为基准数吧。接下来，需要将这个序列中所有比基准数大的数放在6的右边，比基准数小的数放在6的左边，类似下面这种排列。

      3  1  2  5  4  6  9  7  10  8

 

在初始状态下，数字6在序列的第1位。我们的目标是将6挪到序列中间的某个位置，假设这个位置是k。现在就需要寻找这个k，并且以第k位为分界点，左边的数都小于等于6，右边的数都大于等于6。想一想，你有办法可以做到这点吗？

方法其实很简单，

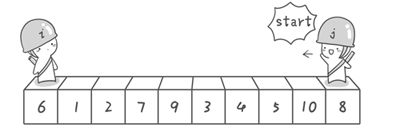
1.分别从初始序列“6  1  2 7  9  3  4  5 10  8”两端开始“探测”。先从右往左找一个小于6的数，再从左往右找一个大于6的数，然后交换他们。这里可以用两个变量i和j，分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵i”和“哨兵j”。刚开始的时候让哨兵i指向序列的最左边（即i=1），指向数字6。让哨兵j指向序列的最右边（即j=10），指向数字8。

 首先哨兵j开始出动。因为此处设置的基准数是最左边的数，所以需要让哨兵j先出动，这一点非常重要（请自己想一想为什么）。哨兵j一步一步地向左挪动（即j--），直到找到一个小于6的数停下来。

 

2.接下来哨兵i再一步一步向右挪动（即i++），直到找到一个数大于6的数停下来。最后哨兵j停在了数字5面前，哨兵i停在了数字7面前。

 

现在交换哨兵i和哨兵j所指向的元素的值。交换之后的序列如下。

6  1  2  5  9  3  4  7  10  8

 

 

 

 

3.第一次交换结束。接下来开始哨兵j继续向左挪动（再友情提醒，每次必须是哨兵j先出发）。他发现了4（比基准数6要小，满足要求）之后停了下来。哨兵i也继续向右挪动的，他发现了9（比基准数6要大，满足要求）之后停了下来。此时再次进行交换，交换之后的序列如下。

6  1  2  5  4  3  9  7 10  8

 

第二次交换结束，“探测”继续。哨兵j继续向左挪动，他发现了3（比基准数6要小，满足要求）之后又停了下来。哨兵i继续向右移动，糟啦！此时哨兵i和哨兵j相遇了，哨兵i和哨兵j都走到3面前。说明此时“探测”结束。我们将基准数6和3进行交换。交换之后的序列如下。

3  1  2  5  4  6  9  7  10  8

 

、

到此第一轮“探测”真正结束。此时以基准数6为分界点，6左边的数都小于等于6，6右边的数都大于等于6。回顾一下刚才的过程，其实哨兵j的使命就是要找小于基准数的数，而哨兵i的使命就是要找大于基准数的数，直到i和j碰头为止。

剩下的步骤就是重复上面的过程。

OK，解释完毕。 现在基准数6已经归位，它正好处在序列的第6位。此时我们已经将原来的序列，以6为分界点拆分成了两个序列，左边的序列是“3  1  2  5  4”，右边的序列是“9  7  10  8”。接下来还需要分别处理这两个序列。因为6左边和右边的序列目前都还是很混乱的。不过不要紧，我们已经掌握了方法，接下来只要模拟刚才的方法分别处理6左边和右边的序列即可。现在先来处理6左边的序列现吧。

左边的序列是“3  1  2  5  4”。请将这个序列以3为基准数进行调整，使得3左边的数都小于等于3，3右边的数都大于等于3。好了开始动笔吧。

如果你模拟的没有错，调整完毕之后的序列的顺序应该是。

 

2  1  3  5  4

 

OK，现在3已经归位。接下来需要处理3左边的序列“2 1”和右边的序列“5 4”。对序列“2 1”以2为基准数进行调整，处理完毕之后的序列为“1 2”，到此2已经归位。序列“1”只有一个数，也不需要进行任何处理。至此我们对序列“2 1”已全部处理完毕，得到序列是“1 2”。序列“5 4”的处理也仿照此方法，最后得到的序列如下。

 

1  2  3  4  5  6  9  7  10  8

 

       对于序列“9  7  10  8”也模拟刚才的过程，直到不可拆分出新的子序列为止。最终将会得到这样的序列，如下。

 

1  2  3 4  5  6  7  8  9  10

 1 #快速排序 传入列表、开始位置和结束位置
 2 def quick_sort( li , start , end ):
 3     # 如果start和end碰头了，说明要我排的这个子数列就剩下一个数了，就不用排序了
 4     if not start < end :
 5         return
 6 
 7     mid = li[start] #拿出第一个数当作基准数mid
 8     low = start   #low来标记左侧从基准数始找比mid大的数的位置
 9     high = end  #high来标记右侧end向左找比mid小的数的位置
10 
11     # 我们要进行循环，只要low和high没有碰头就一直进行,当low和high相等说明碰头了
12     while low < high :
13         #从high开始向左，找到第一个比mid小或者等于mid的数，标记位置,（如果high的数比mid大，我们就左移high）
14         # 并且我们要确定找到之前，如果low和high碰头了，也不找了
15         while low < high and li[high] > mid :
16             high -= 1
17         #跳出while后，high所在的下标就是找到的右侧比mid小的数
18         #把找到的数放到左侧的空位 low 标记了这个空位
19         li[low] = li[high]
20         # 从low开始向右，找到第一个比mid大的数，标记位置,（如果low的数小于等于mid，我们就右移low）
21         # 并且我们要确定找到之前，如果low和high碰头了，也不找了
22         while low < high and li[low] <= mid :
23             low += 1
24         #跳出while循环后low所在的下标就是左侧比mid大的数所在位置
25         # 我们把找到的数放在右侧空位上，high标记了这个空位
26         li[high] = li[low]
27         #以上我们完成了一次 从右侧找到一个小数移到左侧，从左侧找到一个大数移动到右侧
28     #当这个while跳出来之后相当于low和high碰头了，我们把mid所在位置放在这个空位
29     li[low] = mid
30     #这个时候mid左侧看的数都比mid小，mid右侧的数都比mid大
31 
32     #然后我们对mid左侧所有数进行上述的排序
33     quick_sort( li , start, low-1 )
34     #我们mid右侧所有数进行上述排序
35     quick_sort( li , low +1 , end )
36  
37 
38 #ok我们实践一下
39 if __name__ == '__main__':
40     li = [5,4,3,2,1]
41     quick_sort(li , 0 , len(li) -1 )
42     print(li)

4. 算法分析

优点：速度快，剩空间，缺点：非常脆弱，在实现时一定要注意几个小细节。

什么情况下是最好的呢：

待排序列升序有序O(n)，即，1  2  3  4  5  6  7，这种情况下，基准选择第一个数，调整次数最少，注意只是调试次数减少，比较次数没变少，

所以从理论上来说，比较只需要把数据放入寄存器，然后比较。

mov ax,
mov cx,
cmp ax,cx

但实际情况下，因为有L1，L2的存在，然后你的程序又存在进程切换，现场恢复等等各种复杂因素，实际上的速度就好说了。

 

什么情况下是最差的呢：

待排序序列降序有序O(n²)，即，7  6  5  4  3  2  1，这种情况就退化为冒泡排序。

5.瞎逼逼

快速排序，在排完第一遍的时候，你所选择的基准数就是该数在排序序列中的真实位置。

所以可以瞎想一下，如果基准选择准确，是否可以几次遍历就求出一个无序序列的中位数呢？？？

 

转载请注明——redbear博客