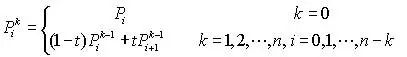前言
贝塞尔曲线是一个强大而又神秘的东西。今天有时间彻底梳理了一下,神秘的面纱被揭下来了,剩下了只有强大。下面就一步一步来了解一下贝塞尔曲线。
贝塞尔曲线是什么
贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线,贝兹曲线由线段与节点组成,节点是可拖动的支点,线段像可伸缩的皮筋,我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线,在一些比较成熟的位图软件中也有贝塞尔曲线工具,如PhotoShop等。在Flash4中还没有完整的曲线工具,而在Flash5里面已经提供出贝塞尔曲线工具。
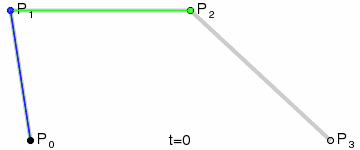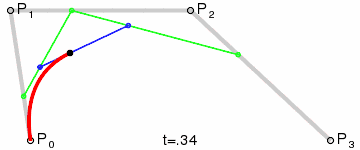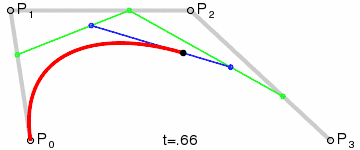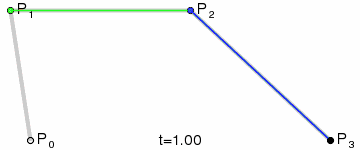
上面是网上找的定义,算了还是看图体会吧。
看了这图后对贝塞尔曲线差不多就有点数了。
Android中实现贝塞尔曲线的API
了解自定义View的小伙伴,肯定知道 canvas.drawPath(),这个方法。该方法接受的第一个对象是Path,这个Path,提供了两个方法:quadTo()、cubicTo(),分别实现二阶贝塞尔曲线、三阶贝塞尔曲线。接下来我们就写代码来看看效果。
quadTo()的使用
代码:
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
Path path = new Path();
path.moveTo(50, 200);
path.quadTo(150, 50, 400, 200);
canvas.drawPath(path, paint);
}
效果:
标注有点简陋,聪明的你,应该看得懂的哈。
cubicTo()的使用
代码:
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
Path path = new Path();
path.moveTo(50, 200);
path.cubicTo(100, 50, 350, 50, 500, 200);
canvas.drawPath(path, paint);
}
效果:
以上就是用Android API实现二阶贝塞尔曲线和三阶贝塞尔取消,是不是很简单呢。
作为一名有梦想的程序员,你一定不会满足的。接下来就研究一下贝塞尔曲线的原理。
贝塞尔曲线公式。
1.贝塞尔曲线的通用公式
在网上查资料得到这个公式,这个公式是贝塞尔曲线的通用公式,通过这个公式可以得到一阶、二阶、三阶。。。。N阶贝塞尔曲线。
第一眼看到这个公式,说实话我是一脸懵逼,心想这好像是微积分吧,当年的高数都是睡过来的。于是求助了在上研究生的同学。
于是得到了下面的图片:
好吧,还是有点懵逼,主要是字太丑。
不管推导过程了,直接把结果拿来用吧。
一阶贝塞尔公式
给定p0、p1两个点。得到如下公式
二阶贝塞尔公式
二阶贝塞尔曲线可以理解为两个一阶贝塞尔曲线的连线上,动态的划出一阶贝塞尔曲线。
三阶贝塞尔曲线
按照二阶的推导原理,以此类推,由四个控制点定义的三阶贝塞尔曲线P03可被定义为分别由(P0,P1,P2)和(P1,P2,P3)确定的两条二阶贝塞尔曲线的线性组合:P03 = (1-t)P02 + tP12
可递归代入得出三阶贝塞尔曲线公式:
贝塞尔曲线原理部分借鉴于:http://mp.weixin.qq.com/s/l0ABkX3IzBk_s8-nWkUJig
在此对大神表示感谢。
计算贝塞尔曲线的路径
通过上面的学习,我们可以很轻松的画出二阶、三阶贝塞尔曲线。那么,我们想画出高阶的贝塞尔曲线呢?我们只是需要贝塞尔曲线的路径而不只是画出细线呢?
那么我们就需要得到贝塞尔曲线的绘制过程,也就是说要得到贝塞尔曲线上的每一个点。
这里不多将直接上代码来,看效果好了。
核心代码,计算贝塞尔曲线上的点集:
借鉴于https://github.com/venshine/BezierMaker
这是真大神,给跪了。
/**
* 创建Bezier点集
*
* @return
*/
private ArrayList buildBezierPoints() {
ArrayList points = new ArrayList<>();
int order = mControlPoints.size() - 1;
float delta = 1.0f / FRAME;
for (float t = 0; t <= 1; t += delta) {
// Bezier点集
points.add(new PointF(deCasteljauX(order, 0, t), deCasteljauY(order, 0, t)));
}
return points;
}
/**
* deCasteljau算法
*
* @param i 阶数
* @param j 点
* @param t 时间
* @return
*/
private float deCasteljauX(int i, int j, float t) {
if (i == 1) {
return (1 - t) * mControlPoints.get(j).x + t * mControlPoints.get(j + 1).x;
}
return (1 - t) * deCasteljauX(i - 1, j, t) + t * deCasteljauX(i - 1, j + 1, t);
}
/**
* deCasteljau算法
*
* @param i 阶数
* @param j 点
* @param t 时间
* @return
*/
private float deCasteljauY(int i, int j, float t) {
if (i == 1) {
return (1 - t) * mControlPoints.get(j).y + t * mControlPoints.get(j + 1).y;
}
return (1 - t) * deCasteljauY(i - 1, j, t) + t * deCasteljauY(i - 1, j + 1, t);
}
初始化控制点:
void init() {
mControlPoints = new ArrayList<>(MAX_COUNT + 1);
int w = getResources().getDisplayMetrics().widthPixels;
mControlPoints.add(new PointF(144, 144));
mControlPoints.add(new PointF(266, 51));
mControlPoints.add(new PointF(500, 83));
mControlPoints.add(new PointF(650, 212));
mControlPoints.add(new PointF(689, 491));
mControlPoints.add(new PointF(485, 747));
mControlPoints.add(new PointF(185, 577));
mControlPoints.add(new PointF(45, 180));
mControlPoints.add(new PointF(48, 747));
mControlPoints.add(new PointF(689, 747));
//在这里初始化控制点的集合,可以任意添加控制点,从而得到N阶贝塞尔曲线。
paint = new Paint();
paint.setAntiAlias(true);
paint.setStyle(Paint.Style.STROKE);
paint.setColor(getResources().getColor(R.color.colorAccent));
}
在onDraw方法中调用:
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
Path path = new Path();
ArrayList list = buildBezierPoints();
for (int i = 1; i < list.size(); i++) {
path.moveTo(list.get(i - 1).x, list.get(i - 1).y);
path.lineTo(list.get(i).x, list.get(i).y);
canvas.drawPath(path, paint);
}
}
好了看下效果,由于控制点是随便添加的,所以就是这样的鬼样子:
看到这里大家觉得没什么了不起的。大家可以发挥想象力。
1.坐标规划的够好,就可以画出各种各样的图案,画个汽车不成问题。
2.得到贝塞尔曲线的点集后,我们不一次性画出来,而是延时的画,那么就可以让线条动起来,那么就是动画了
3.得到贝塞尔曲线后,我们不划线,而是在这个路径上画图案,那么就可以实现,图案在这路径上飘动。就想直播里面点赞出现的动画一样。