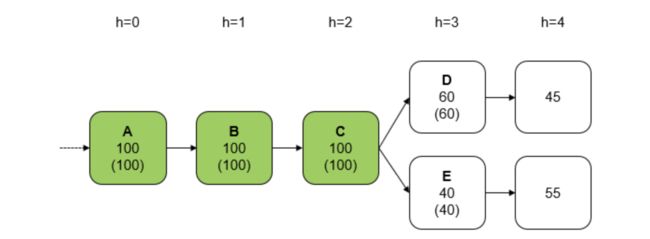
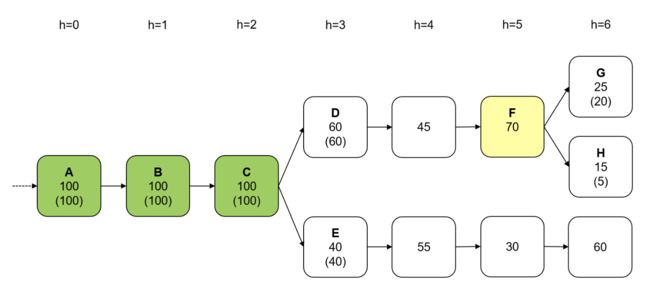
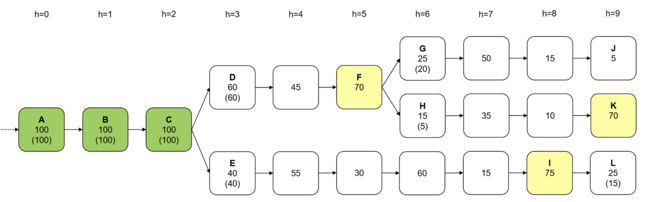
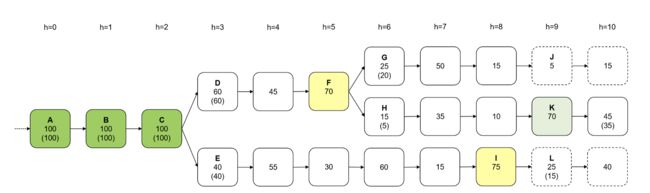
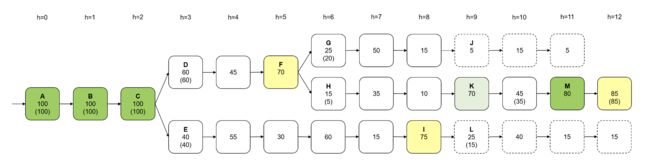
市面上有多个版本的Casper,文档分散,同时技术本身也在不断反占中。现在大家正在对分片版本进行拼接 - 即使这些不同的版本没有一个是对的,它也还是很重要。 但是如果你把证据放在一边,我认为它在操作中的样子 (至少它的本质 ) 非常直观。 这是我如何理解Casper工作的简化了的思路图。
(这里有各种重要的警告,我将在底部列出。它们归结为:其中一些可能是错误的; 我不是Casper的专家,旨在抛砖引玉。)
Casper的投票演练
通常情况下,在链上一次添加一个区块,所有人都投票支持它,此动作顺利完成,一切都很常规。
但是,偶尔会出现在相同高度竞争的区块会导致分叉,这可能由不同的原因导致的:比如网络延时,临时网络分区,受到攻击或者别的原因。
当发生分叉时,可能需要进行几轮投票才能收到达到提名要求的三分之二票数的最终确认。 即使一个区块获得了提名,它也可能无法在下一轮获得2/3的投票确认。 (选民可能会尝试在每一轮投票给一个区块,但包括最后的投票是可选的 - 也就是说可以有100票,但最终所有投的区块都没有被确认。)
然而,至关重要的是,即使失败的提名也会对其选民产生影响。 一位有权决定最终确定被提名人的选民不能投票支持另外一个有冲突的被提名人 (即:一个不是他们投票决定的提名者 ) 直到一个新提名者被其他选民提名。 一个违反这种规则的投票者会被取缔,即失去他们的投票权重!
最终,部分被提名人会获得超过1/3的最终选票。 这是一个至关重要的转折点,因为在此之后,没有冲突的分支可以赢得2/3提名而不会让一些对手被取缔。 因此,一旦一个区块超过1/3的最终投票,没有与该区块冲突的分支可能会被提名和最终被确定。
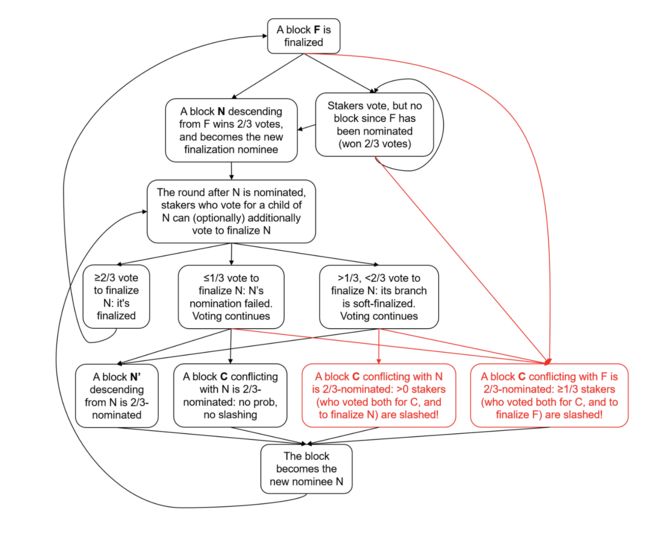
总体流程思路如下:
如果存在分叉,则每个投票者都会投票,直到N区获得2/3票并成为当前的被提名人。
在N获得2/3之后的回合中,投票者有(可选)机会通过投票来确定N。
这三个步骤是:
a)N得到≥2/ 3的最终投票:N被最终确定,并且链被重新统一。
b)N得到> 1/3,<2/3终结投票:未最终确定,但N的分支是软定型的 - 最终确定的块很可能是N的继任者。
c)N得到≤1/ 3的最终投票:未最终确定。 投票恢复,直到另一名被提名者获得2/3(并且可能与N互为冲突提名人)。
该状态转换图总结了该流程:
取缔条件
正如Casper FFG论文中所描述(并证明)的那样,条件是为了确保理想的性能:
“Accountable safety”:在选票≥1/ 3基本上,如果没有冲突块同时被确认的情况,就不会有区块被取缔。
“Plausible liveness”:最终确认的动作永远不会被“卡住”,因为系统只有在有人出局的情况下才能得出晋级结果。
但另一种看待取缔条件的方法是,它们强制执行上面提到的被提名人投票逻辑(在投票完成一个确认结果后没有投票给新的被提名人等),并且通过该逻辑确保这些属性。 特别是,虽然FFG论文的第一个出局条件是常识(你每轮只能投票一次),但第二个 (不跨越原则 ) 更令人困惑:“你的投票不能跨越另一个提名人。”
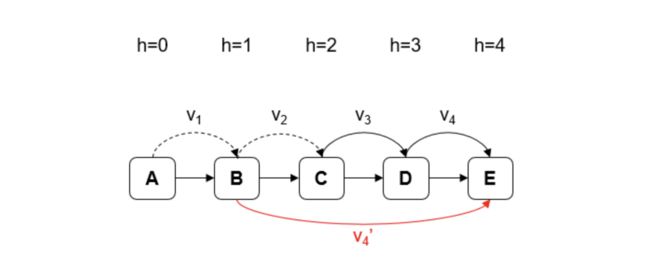
在Casper FFG中,每个投票都指定一个目标区块(您正在投票的区块)和一个源区块(先前获得2/3投票的目标的祖块)。 无跨越规则意味着,如果您对高度为7的目标区块(拥有高度为5的区块源)进行投票,则无法对高度≥8而区块源≤高度4的目标投下另一个投票: 第二次投票跨越第一次。
不跨越规则与我在上面的演练中引用的无规则并不完全相同(简而言之,“投票完成后,不能投票支持相互冲突的新候选人”):
无违反(No-reneging)规则:作为一个选民,如果出现以下情况,你会被出局:
1.你投票(在高度h)完成对A区块(高度为h-1)的确认; 以及
2.之后(即,在高度h + k),你投票给B区块,但是与A冲突; 以及
3. A和B之间没有B的共同祖先块(即,在高度≥h, 然而,事实证明,无跨越规则意味着无违反规则。 因此,由于Casper FFG强制实施无跨越规则,因此无违反规则也适用。 虽然这两条规则并不完全相同: 我认为“无违反规则”更直观,也更可取,因为它消除了投票中令人困惑的源参数。 然而,上述第三条关于无违反规者定义(“没有B的祖先块......”)可以说比没有跨越的规则更加笨拙。 实施第3条的一种方法是采用多步骤削减协议:我向你的选票发布一个挑战(最终确定A,投票给B); 你有一段时间(例如一个月)来回应一个A区块<高度 在任何情况下,无跨越规则或无违反规则都会推导出上面演练中描述的被提名者投票逻辑。 正如Patrick Dugan所指出的那样,这些规则,尤其是无违反规则,在先前的共识协议中有明确的先例,如Jae Kwon的Tendermint及他们的锁定规则:“一旦验证器预先提交了一个块,它就被锁定在该块上。 然后,1)它必须在它被锁定的块上出现 2)它只能解锁,并且如果在后一轮中有该块的Polka[2/3投票],则预先设置新块。“ 根据一般的要求,这里有证据表明,无违反规则确保了可靠的安全性和合理的活力,正如FFG的无跨越规则所做的那样。 安全性:我们想表明,如果两个冲突的块都已完成时,≥1/ 3的投票者会被取缔。 假设两个块在高度h处为A,在高度h + k处为B。另设B'在高度h + j是B(或B本身)的祖先,最低高度> h,得到2/3选票。 (由于B本身得到2/3选票票,所以总有至少一个这样的块:B)直接来自这个定义,A和B之间的B'的祖先没有2/3票,而且B'冲突。 因此,根据无违规规则,≥1/3的投票者投票支持A和B'的将会被取缔。 活跃度:我们希望展示一些新的更高高度的区块总是可以在没有任何人被取缔的情况下完成,只要新的区块不断被添加进来。 但这个证明很简单:现任被提名人的后代(即获得2/3票数的最高高度的块)可以随时投票,然后由100%的投票最终确定而不违反“无违反规则“。 (该规则仅阻止已经最终确定的投票,其曾经对提名冲突的被提名人进行投票行为:一旦获得2/3投票,就像现任被提名人一样,他们可以自由投票。) 没有跨越意味着没有违反:作为彩蛋,这里有一个证明,任何违反“无违反规则”的行为也违反了“无跨越规则”。 假设你违反了“无违反规则”,意思是:1)你在高度h投票以在h-1确认A;2)最后(即,在高度h + k)你投票给冲突区块B;以及3)在 获得2/3投票的A和B之间没有祖先块B’。 由于投票来源必须有2/3的投票,因此您投票给B的源必须是高度h-1-j:即低于A的高度。所以,您投票支持B(高度h + k ,源高度h-1-j)跨越您的投票以完成A(高度h,源高度h-1)。 1)此文档仅代表我的理解,可能包含错误 - 如果是,请告诉我们! 我不是Casper专家。 2)这是为了理清对Casper有了一定模糊认识的人一些理解程度。如果你是完全的菜鸟,你可能会发现这些有助于你对以下作品的延展阅读:以太坊证明的常见问题解答;Blockgeeks的Casper速成课程;jon choi的Casper 101和Casper FFG论文。 3)我故意简化了一些重要阐述。 例如:Casper FFG在检查点(checkpoints)上运行,而不是在每个区块上运行,因为如果通过投票来最终确定每个区块会产生大量开销而几乎没有任何利润。 但是没有概念上的理由说明算法不适用于每个块:检查点(checkpionts)实际上代表每100个块。 为了简单起见,我通过区块来进行前后说明。 4)我谈论“之前”和“之后”,例如,“在投票决定A之后,没有对新的冲突提名人B进行投票。”但在实践中,很难对时间进行强制执行:因为当我发现你在v2之前对v1进行投票,这并不意味着你按照那个顺序发送它们。 因此,当我在这篇文章中使用“之后”时,我的意思是它是“在更高的区块高度”的简写。 换句话说,我假设投票者是按照高度递增的顺序投票 - 诚信的投票者应该会这样做。 但“取缔规则”不能真正强制时间的先后,只能实现对高度进行处理。 5)我假设每一个投票者都在每一轮投票,这套投票者规则永远不会改变。 我不认为删除这些假设中的任何一个对上述的这些论点有严重的影响,但这会使它们变得更加混乱。 6)在演练的部分内容中,我几近假设投票者不会做出让自己被取缔的行为(投票)。 当然有恶意攻击者愿意接受被取缔的后果,但是这些攻击肯定是非常罕见的,我的主要目标是在“大部分时间”显示Casper的操作过程。 7)我已经使用了一些特殊的术语,我发现它更清晰或更简洁 - “被提名者”而不是“被证明者”,“投票者”而不是“验证者”等。如果对此引起的任何混淆表示抱歉。 这篇文章的大部分内容只是想在推特中发表的最新想法。 感谢Justin Drake,@ matthew_d_green,Dan Robinson,Danny Ryan和其他人和我进行的有益的讨论和更正。 还有Jane对Ritual de lo Habitual的永恒下半部分的执着,这帮助我完成了这项任务。证明
说明