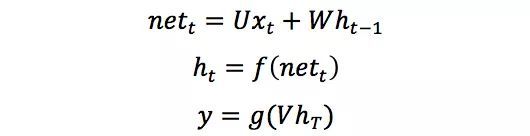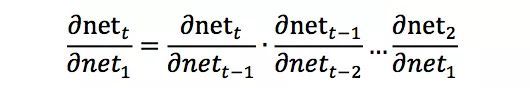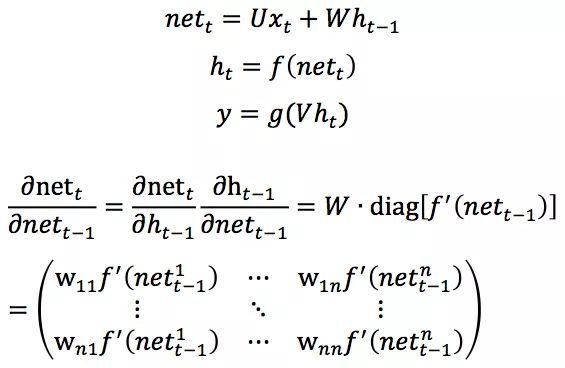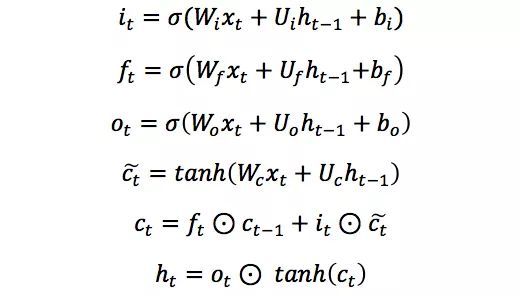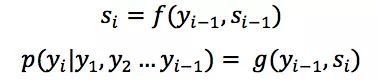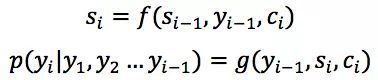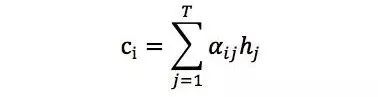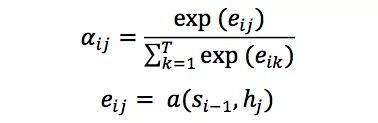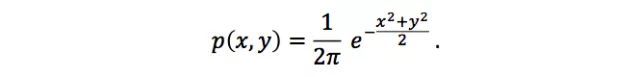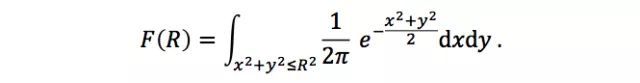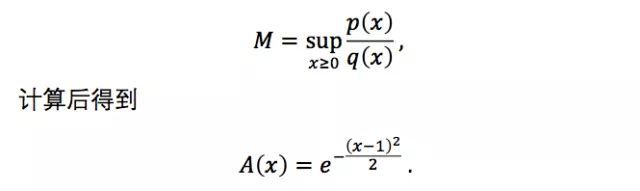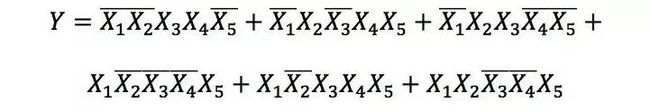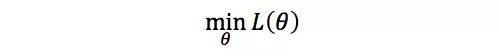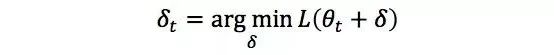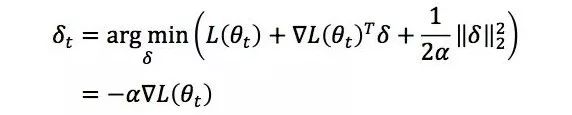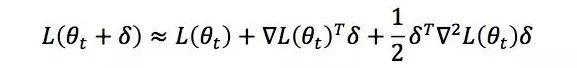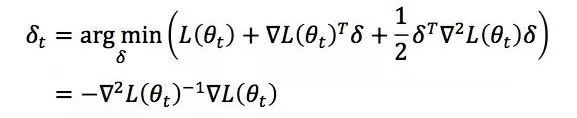9. 循环神经网络
场景描述
循环神经网络(Recurrent Neural Network)是一种主流的深度学习模型,最早在20世纪80年代被提出 ,目的是建模序列化的数据。我们知道,传统的前馈神经网络一般的输入都是一个定长的向量,无法处理变长的序列信息,即使通过一些方法把序列处理成定长的向量,模型也很难捕捉序列中的长距离依赖关系。而RNN通过将神经元串行起来处理序列化的数据,比如文本的词序列、音频流和视频流序列等。由于每个神经元能用它的内部变量保存之前输入的序列信息,使得整个序列可以被浓缩成抽象的表示,并可以据此进行分类或生成新的序列。近年来,得益于计算能力的大幅提升和网络设计的改进(LSTM、GRU、Attention机制等),RNN在很多领域取得了突破性的进展。比如机器翻译、序列标注、图像描述、视频推荐、智能聊天机器人、自动作词作曲等,给我们的日常生活带来了不少便利和乐趣。
问题描述
- 什么是循环神经网络?如何用它产生文本表示?
- RNN为什么会出现梯度的消失或爆炸?有什么样的改进方案?
解答与分析
1. 什么是循环神经网络?如何用它产生文本表示?
传统的前馈神经网络,包括卷积神经网络(Convolutional Neural Network, CNN)在内,一般都是接受一个定长的向量作为输入。比如在做文本分类时,我们可以将一篇文章所对应的TF-IDF(Term Frequency-Inverse Document Frequency)向量作为前馈神经网络的输入,其中TF-IDF向量的维度是词汇表的大小。显而易见,这样的表示实际上丢失了输入的文本序列中每个单词的顺序。在用卷积神经网络对文本进行建模时,我们可以输入变长的字符串或者单词串,然后通过滑动窗口+Pooling的方式将原先的输入转换成一个固定长度的向量表示;这样做可以捕捉到原文本中的一些局部特征,但是两个单词之间的长距离依赖关系还是很难被学习到。
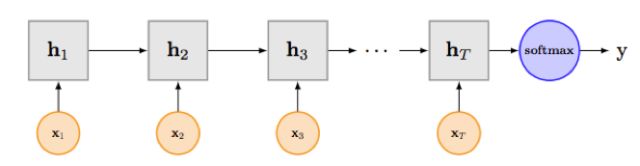
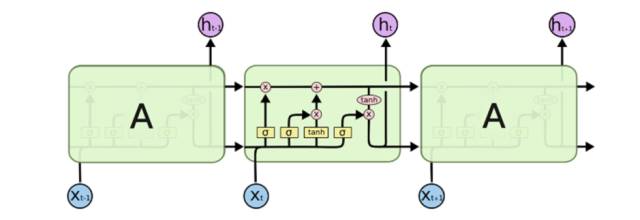
RNN(Recurrent Neural Network,循环神经网络)的目的便是处理像文本这样变长并且有序的输入序列。它模拟了人阅读一篇文章的顺序,从前到后阅读文章中的每一个单词,并且将前面阅读到的有用信息编码到状态变量中去,从而拥有了一定的记忆能力,可以更好地理解之后的文本。下图展示了一个典型RNN的网络结构[1]:
其中f和g为激活函数,U为输入层到隐含层的权重矩阵,W为隐含层从上一时刻到下一时刻状态转移的权重矩阵,在文本分类任务中(如上图),f可以选取Tanh或者ReLU函数,g可以采用Softmax函数,更多关于激活函数的细节可以参见[2]。
2. RNN为什么会出现梯度的消失或爆炸?有什么样的改进方案?
RNN模型的求解可以采用BPTT(Back Propagation Through Time)算法实现 ,实际上是反向传播(Back Propagation)算法的简单变种;如果将RNN按时间展开成T层的前馈神经网络来理解,就和普通的反向传播算法没有什么区别了。RNN的设计初衷之一就是能够捕获长距离输入之间的依赖。从结构上来看,RNN也绝对能够做到这一点。然而实践发现,使用BPTT算法学习的RNN并不能成功捕捉到长距离的依赖关系,这一现象可以用梯度消失来解释。传统的RNN梯度可以表示成连乘的形式:
其中
由于预测的误差是沿着神经网络的每一层反向传播的,因此当Jacobian矩阵的最大特征值大于1时,随着离输出越来越远,每层的梯度大小会呈指数增长,导致梯度爆炸(gradient explosion);反之,若Jacobian矩阵的最大特征值小于1,梯度的大小会呈指数缩小,即产生了梯度消失(gradient vanishing)。对于普通的前馈网络来说,梯度消失导致无法通过加深网络层次来改善神经网络的预测效果,因为无论如何加深网络,只有靠近输出的若干层才真正起到的学习的作用。对于RNN来说,这导致模型很难学习到输入序列中的长距离依赖关系。
梯度爆炸的问题可以通过梯度裁剪(Gradient Clipping)来缓解,也就是当梯度的范式大于某个给定值时,对梯度进行等比收缩;而梯度消失问题相对比较棘手,需要对模型本身进行改进。 ResNet[3]是对前馈神经网络的改进,通过残差学习的方式缓解了梯度消失的现象,从而使得我们能够学习到更深层的网络表示;而对于RNN来说,LSTM(Long short-term memory)[4]及其变种GRU(Gated recurrent unit)[5]等模型通过加入门控机制(Gate),很大程度上改善了梯度消失所带来的损失。关于ResNet和LSTM的细节会在其他章节介绍,敬请期待。
参考文献:
[1] Liu, Pengfei, Xipeng Qiu, and Xuanjing Huang. "Recurrent neural network for text classification with multi-task learning." arXiv preprint arXiv:1605.05101 (2016).
[2] https://en.wikipedia.org/wiki/Activation_function
[3] He, Kaiming, et al. "Deep residual learning for image recognition." Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.
[4] Hochreiter, Sepp, and Jürgen Schmidhuber. "Long short-term memory." Neural computation 9.8 (1997): 1735-1780.
[5] Chung, Junyoung, et al. "Empirical evaluation of gated recurrent neural networks on sequence modeling." arXiv preprint arXiv:1412.3555 (2014).
10.LSTM
场景描述
俗话说,前事不忘,后事之师,各种带有记忆功能的网络是近来深度学习研究和实践的一个重要领域。由于RNN有着梯度弥散(vanishing gradient)和梯度爆炸(explosion gradient)等问题,难以学习长期的依赖,在遇到重要的信息时,又难以清空之前的记忆,因此在实际任务中的效果往往并不理想。
LSTM是Long Short-Term Memory(长短期记忆网络)的简称。作为RNN的最知名和成功的扩展,LSTM可以对有价值的信息进行长期记忆,并在遇到新的重要信息时,及时遗忘过去的记忆,减小了RNN的学习难度。它在语音识别,语音建模,机器翻译,图像描述生成,命名实体识别等各类问题中,取得了巨大的成功。
问题描述
LSTM是如何实现长短期记忆功能的?
它的各模块分别使用了什么激活函数,可以使用别的激活函数么?
背景知识假设:基本的深度学习知识。
该类问题的被试者:对RNN有一定的使用经验,或在自然语言理解、序列建模等领域有一定的经历。
解答与分析
1. LSTM是如何实现长短期记忆功能的?
该问题需要被试者对LSTM的结构有清晰的了解,并理解其原理。在回答的过程中,应当结合其结构图或更新的计算公式进行讨论,LSTM的结构图示例如下:
图片来源:http://colah.github.io/posts/2015-08-Understanding-LSTMs/
与传统的RNN比较,LSTM仍然是基于xt和ht-1来计算ht,只不过对内部的结构进行了更加精心的设计,加入了三个阀门(输入门i, 遗忘门f,输出门o)和一个内部记忆单元c。输入门控制当前计算的新状态以多大程度更新到记忆单元中;遗忘门控制前一步记忆单元中的信息有多大程度被遗忘掉;输出门控制当前的输出有多大程度上取决于当前的记忆单元。
经典的LSTM中,第t步的更新计算公式如下:
其中输入门it是通过输入xt和上一步的隐含层输出ht-1进行线性变换,再经过Sigmoid激活函数得到。输入门的结果是向量,其中每个元素是0到1之间的实数,用于控制各维度流过阀门的信息量;Wi,Ui两个矩阵和向量bi为输入门的系数,是在训练过程中需要学习得到的。遗忘门ft和输出门ot的计算方式与输入门类似,它们有各自的系数W,U和b。与传统RNN不同的是,从上一个记忆单元的状态ct-1到当前的状态ct的转移不完全取决于由tanh激活函数计算得到状态,而是由输入门和遗忘门来共同控制。
在一个训练好的网络中,当输入的序列中没有重要信息时,LSTM的遗忘门的值接近于1,输入门的值接近于0,此时过去的记忆会被保存,从而实现了长期记忆功能;当输入的序列中出现了重要的信息时,LSTM应当把其存入记忆中,此时其输入门的值会接近于1;当输入的序列中出现了重要信息,且该信息意味着之前的记忆不再重要时,此时输入门的值接近1, 遗忘门的值接近于0,这样旧的记忆被遗忘,新的重要信息被记忆。经过这样的刻意设计,可以使得整个网络更容易学习到序列之间的长期依赖。
2. LSTM里各模块分别使用什么激活函数,可以使用别的激活函数么?
LSTM中,遗忘门、输入门和输出门使用Sigmoid函数作为激活函数;在生成候选记忆时,使用双曲正切函数tanh作为激活函数 。Sigmoid函数的输出在0~1之间,符合门控的物理定义,且当输入较大/较小时,其输出会非常接近1/0,从而保证该门开/关。在生成候选记忆时使用tanh函数,是因为其输出在-1~1之间,这与大多数场景下特征的分布是0中心的相吻合。此外,tanh函数在输入为0附近相比Sigmoid函数有更大的梯度,通常使模型收敛更快。
LSTM的激活函数也不是一成不变的。例如在原始的LSTM中[1],使用的激活函数是Sigmoid函数的变种,h(x)=2sigmoid(x)-1,g(x)=4sigmoid(x)-2,这两个函数的范围分别是[-1,1]和[-2,2]。并且在原始的LSTM中,只有输入门和输出门,没有遗忘门,其中输入x经过输入门后是直接与记忆相加的,所以输入门控g(x)的值是0中心的。后来经过大量的研究和实践,发现增加遗忘门对LSTM的性能有很大的提升[4],并且h(x)使用tanh比2*sigmoid(x)-1要好,所以现代的LSTM采用Sigmoid和tanh作为激活函数。事实上在门控中,使用Sigmoid函数是几乎所有现代神经网络模块的常见选择:例如在GRU[2]和注意力机制中,也广泛使用Sigmoid作为门控的激活函数。因为门控的结果要与被控制的信息流按元素相乘,所以门控的激活函数通常是会饱和的函数。
此外,在一些对计算能力有限制的情景,诸如可穿戴设备中。由于Sigmoid函数中求指数需要一定的计算, 此时会使用hard gate,让门控输出为0或1的离散值:即当输入小于阈值时,门控输出为0,大于阈值时,输出为1。从而在性能下降不显著的情况下,减小计算量。
总而言之,LSTM经历了20年的发展,其核心思想一脉相承,但各个组件都发生了很多演化。了解其发展历程和常见变种,可以让我们在实际工作和研究中,结合问题选择最佳的LSTM模块。灵活思考并知其所以然,而不是死背网络的结构和公式,也有助于在面试中取得更好的表现。
参考文献:
[1] Hochreiter, Sepp, and Jürgen Schmidhuber. "Long short-term memory." Neural computation 9.8 (1997): 1735-1780.
[2] Chung, Junyoung, et al. "Empirical evaluation of gated recurrent neural networks on sequence modeling." arXiv preprint arXiv:1412.3555 (2014).
[3] Gers, Felix A., and Jürgen Schmidhuber. "Recurrent nets that time and count." IJCNN 2000
[4] Gers, Felix A., Jürgen Schmidhuber, and Fred Cummins. "Learning to forget: Continual prediction with LSTM." (1999): 850-855.
11.Seq2Seq
场景描述
作为生物体,我们的视觉和听觉会不断地获得带有序列的声音和图像信号,并交由大脑理解;同时我们在说话、打字、开车等过程中,也在不断地输出序列的声音、文字、操作等信号。在互联网公司日常要处理的数据中,也有很多是以序列形式存在的,例如文本、语音、视频、点击流等等。因此如何更好的对序列进行建模,一向是研究的要点。
2013年来,随着深度学习的发展,Seq2Seq(sequence to sequence,序列到序列)框架在机器翻译领域被大量采用,随后迅速影响到了上述的各领域,应用在了各类序列数据上。
问题描述
1. Seq2Seq的框架是什么?有哪些优点?
2. Seq2Seq在解码时,有哪些常用的方法?
背景知识假设:基本的深度学习知识。
该类问题的被试者:对RNN有一定的使用经验,或在自然语言理解、序列建模等领域有一定的经历。
解答与分析
1. Seq2Seq的框架是什么?有哪些优点?可以结合具体的应用场景进行分析。
在Seq2Seq框架提出之前,深度神经网络在图像分类等问题上取得了非常好的效果。在其擅长解决的问题中,输入和输出通常都可以表示为固定长度的向量,如果长度稍有变化,会使用补零等操作。然而许多重要的问题,例如机器翻译、语音识别、自动对话等,表示成序列后,其长度事先并不知道。因此如何突破先前深度神经网络的局限,使其可以适应这些场景,成为了13年以来的研究热点,Seq2Seq框架应运而生[1][2]。
Seq2Seq框架的核心思想是:通过深度神经网络将一个作为输入的序列映射为一个作为输出的序列,这一过程由编码输入与解码输出两个环节构成。在经典的实现中,编码器和解码器分别由一个RNN构成,其选择有传统RNN、LSTM、GRU等,这两个RNN是共同训练的。
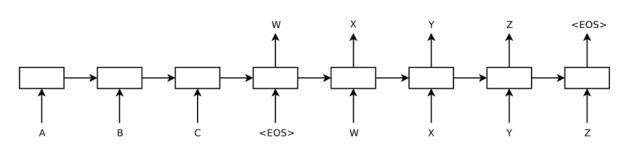
上图[3]是Seq2Seq应用于机器翻译时的例子,输入的序列是一个源语言的句子,有三个单词A、B、C,编码器依次读入A、B、C和结尾符
在文本摘要时,输入的序列是长句子或段落,输出的序列是摘要短句。在图像描述生成时,输入是图像经过视觉网络的特征,输出的序列是图像的描述短句。在语音识别时,输入的序列是音频信号,输出的序列是识别出的文本。这些场景中,编码器或解码器会依据场景有不同的设计,大家在面试时可以结合自己的项目经历展开探讨。
2. Seq2Seq在解码时,有哪些常用的方法?
Seq2Seq最核心的部分是其解码部分,大量的改进也是在解码环节衍生的,因此面试时也常常问到。Seq2Seq最基础的解码方法是贪心法,即选取一种度量标准后,每次都在当前状态下选择最佳的一个结果,直到结束。贪心法的计算代价低,适合作为基础实现(baseline),并与其他方法相比较。很显然贪心法获得的是一个局部最优解,由于实际问题的复杂性,该方法往往并不能取得最领先的效果。
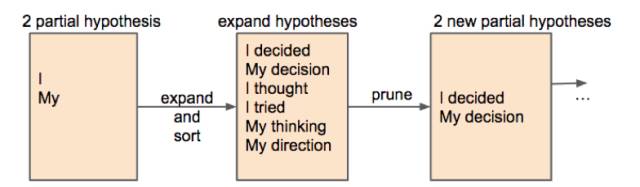
Beam search是常见的改进算法,它是一种启发式的算法。该方法会保存beam size(后面简写为b)个当前的较佳选择,然后解码时每一步根据保存的选择进行下一步扩展和排序,接着选择前b个保存,循环进行,直到结束时选择最佳的一个作为解码的结果。下图为b为2的示例:
在该例中,当前已经有解码得到的第一个词的两个选项:I和My。然后,将I和My输入到解码器,得到一系列候选的序列诸如I decided、My decision、 I thought等。最后,从后续序列中选择最优的两个,作为前两个词的两个选项。很显然,如果b取1,那么会退化为前述的贪心法。随着b的增大,其搜索的空间增大,获得的效果会提高,但需要的计算量也会增大。在实际的应用如机器翻译、文本摘要中,b往往会选择一个适中的范围如8~12。
解码时使用堆叠的RNN、增加dropout机制、与编码器之间建立残差连接等,也是常见的改进措施。大家在研究和工作中,可以依据使用场景,多查阅文献和技术文档,有针对的选择和实践。
在解码环节,另一个重要的改进是注意力机制[4],它的引入使得解码时,每一步可以有针对地关注与当前有关的编码结果,从而减小了编码器输出表示的学习难度,也更容易学到长期的依赖关系。注意力机制会在下一节做更加深入的探讨,敬请期待。此外,解码时还可以采用记忆网络(memory network)[5]等,从外界获取知识。
参考文献:
[1] Auli, Michael, et al. "Joint Language and Translation Modeling with Recurrent Neural Networks." EMNLP. 2013.
[2] Cho, Kyunghyun, et al. "Learning phrase representations using RNN encoder-decoder for statistical machine translation." EMNLP. 2014.
[3] Sutskever, Ilya, Oriol Vinyals, and Quoc V. Le. "Sequence to sequence learning with neural networks." NIPS. 2014.
[4] Bahdanau, Dzmitry, Kyunghyun Cho, and Yoshua Bengio. "Neural machine translation by jointly learning to align and translate." ICLR. 2015.
[5] Sukhbaatar, Sainbayar, Jason Weston, and Rob Fergus. "End-to-end memory networks." NIPS. 2015.
12.注意力机制
场景描述
作为生物体,我们的视觉和听觉会不断地获得带有序列的声音和图像信号,并交由大脑理解;同时我们在说话、打字、开车等过程中,也在不断地输出序列的声音、文字、操作等信号。在互联网公司日常要处理的数据中,也有很多是以序列形式存在的,例如文本、语音、视频、点击流等。因此如何更好的对序列进行建模,一向是研究的要点。
为了解决这些问题,注意力机制(attention mechanism)被引入Seq2Seq模型中。注意力机制模仿人在生成序列时的行为,当解码序列的某个输出时,重点关注输入序列中和当前位置的输出相关的部分,缓解了Seq2Seq模型的上述问题。作为一种通用的思想,注意力机制在包括Seq2Seq在内的多种场景中都得到了应用。
问题描述
RNN的Seq2Seq模型中引入了注意力机制(attention mechanism)是为了解决什么问题?在机器翻译的Seq2Seq模型中使用注意力机制建模时,为什么选用了双向的RNN模型?
背景知识假设:基本的深度学习知识。
该类问题的被试者:对RNN有一定的使用经验,或在自然语言理解、序列建模等领域有一定的经历。
解答与分析
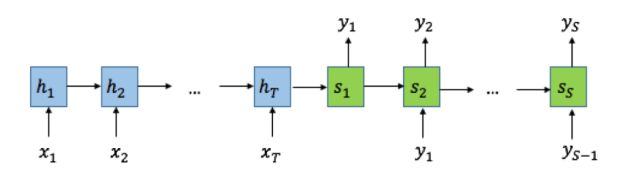
我们已经介绍了Seq2Seq模型以及LSTM。在实际任务,例如机器翻译中,使用Seq2Seq模型,通常会先使用一个RNN作为编码器,将输入序列(源语言句子的词向量序列)编码成为一个向量表示,然后再使用一个RNN模型作为解码器,从编码器得到的向量表示里解码得到输出序列(目标语言句子的词序列)。
Seq2Seq模型中, 当前隐状态以及上一个输出词决定了当前输出词,即:
其中f, g是非线性变换,通常是多层神经网络;yi是输出序列中的一个词,si是对应的隐状态。
Figure 1. Seq2Seq模型
在实际使用中,会发现随着输入序列的增长,模型的性能发生了显著下降。这是因为编码时将输入序列的全部信息压缩到一个向量表示中,随着序列增长,句子越前面的词的信息的丢失就越严重。试想翻译一个有100个词的句子,需要将整个句子全部词的语义信息编码在一个向量中,而在解码时,目标语言的第一个词大概率是和源语言的第一个词相对应的,这就意味着第一步的解码就需要考虑100步之前的信息。建模时的一个小技巧是将源语言句子逆序输入,或者将其重复两遍输入来训练模型,这可以得到一定的性能提升。使用LSTM能够在一定程度上缓解这个问题,但在实践中对于过长的序列仍然难以有很好的表现。
同时,Seq2Seq模型的输出序列中,常常会丢失或者重复部分输入序列的信息。这是因为在解码时,对当前词及对应的源语言词的上下文信息和位置信息也在编码解码过程中丢失了。
Seq2Seq模型中引入注意力机制就是为了解决这些问题。
在注意力机制中,仍然可以用普通的RNN对输入序列进行编码,得到隐状态h1, h2 ... hT,但是在解码时,每一个输出词都依赖于前一个隐状态以及输入序列每一个对应的隐状态:
其中语境向量ci是输入序列全部隐状态h1, h2 ... hT的一个加权和:
权重参数,即注意力权重αij并不是一个固定权重,而是由另一个神经网络计算得到:
神经网络α将上一个输出序列隐状态si-1和输入序列隐状态hj作为输入,计算出一个xj, yi对齐的值eij,再归一化得到权重αij。
Figure 2. 双向RNN的注意力机制模型
我们可以对此给出一个直观的理解:在生成一个输出词时,会考虑每一个输入词和当前输出词的对齐关系,对齐越好的词,会有越大的权重,对生成当前输出词的影响也就越大。下图给出了翻译时注意力机制的权重分布,在互为翻译的词上会有最大的权重。
Figure 3. 注意力机制的权重分布
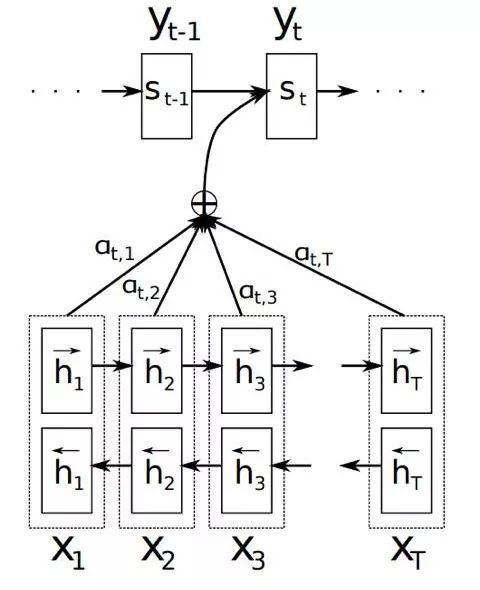
在机器翻译这样一个典型的序列到序列模型里,生成一个输出词yj时,会用到第i个输入词对应的隐状态hi以及对应的attention权重αij,如果只使用一个方向的RNN网络来计算隐状态,那么hi只包含了x0到xi的信息,相当于在αij这里丢失了xi后面的词的信息。而使用双向RNN进行建模,第i个输入词对应的隐状态包含了
前者编码了x0到xi的信息,后者编码了xi及之后所有词的信息,防止了前后文信息的丢失。
注意力机制是一种思想,可以有多种不同的实现方式,在Seq2Seq以外的场景也有不少应用,下图展示了在图像描述文本生成任务中的结果,可以看到在生成对应词时,图片上对应物体的部分有较大的注意力权重。
Figure 4. 注意力机制在图片描述文本生成中的应用
参考文献:
[1] Bahdanau, Dzmitry, Kyunghyun Cho, and Yoshua Bengio. "Neural machine translation by jointly learning to align and translate."
[2] Xu, Kelvin, et al. "Show, attend and tell: Neural image caption generation with visual attention."
[3] Rocktäschel, Tim, et al. "Reasoning about entailment with neural attention."
13.集成学习
场景描述
之前几篇中我们介绍了具体的机器学习模型和算法,集成学习(ensemble learning)更多的是一种组合策略,将多个机器学习模型结合起来,可以称为元算法(meta-algorithm)。
面对一个机器学习问题,通常有两种策略,一种是研发人员尝试各种模型,选择其中表现最好的模型做重点调参优化。这种策略类似于奥运会比赛,通过强强竞争来选拔最优的运动员,并逐步提高成绩。另一种重要的策略是集各家之长,如同贤明的君主广泛的听取众多谋臣的建议,然后综合考虑,得到最终决策。后一种策略的核心,是将多个分类器的结果集成为一个统一的决策。使用这类策略的机器学习方法统称为集成学习。其中的每个单独的分类器称为基分类器。
集成学习可以大致分为两类:
Boosting:这类方法训练基分类器时采用串行的方法,各个基分类器之间有依赖。它的基本思路是将基分类器层层叠加,每一层在训练的时候,对前一层基分类器分错的样本,给予更高的权重。测试时,根据各层分类器的结果的加权得到最终结果。
Bagging:这类方法基分类器之间无强依赖,可以并行。其中很著名的算法之一是基于决策树基分类器的随机森林(Random Forest)。为了让基分类器之间互相独立,将训练集分为若干子集(当训练样本数量较少时,子集之间可能有交叠)。
基分类器有时又称为弱分类器,因为基分类器的错误率要大于集成后的分类器。基分类器的错误,是偏差(Bias)和方差(Variance)两种错误之和。偏差主要是由于分类器的表达能力有限导致的系统性错误,表现在训练误差不能收敛到一个比较小的值。方差则是由于分类器对于样本分布过于敏感,导致在训练样本数较少时,产生过拟合。
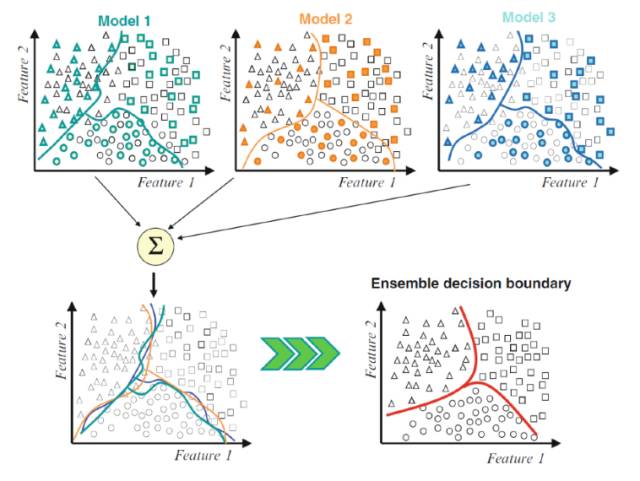
Boosting方法通过逐步聚焦于基分类器分错的样本,减小集成分类器的偏差。Bagging方法则是采取分而治之的策略,通过对训练样本多次采样,并分别训练出多个不同模型,然后做综合,来减小集成分类器的方差。假设每个基分类器出错的概率都是相互独立的,在某个测试样本上,用简单多数的投票方法来集成结果,超过半数基分类器都出错的概率会小于每个单独的基分类器的出错概率。一个Bagging的简单示例如下图:
问题描述
1. 集成学习有哪些基本步骤?
2. 常用的基分类器是什么?
解答与分析
1. 集成学习有哪些基本步骤?请举两个集成学习的例子。
集成学习一般可分为以下三个步骤:
1. 找到误差互相独立的基分类器;
2. 训练基分类器;
3. 合并基分类器的结果。
合并基分类器的方法有voting和stacking两种。前者是用投票的方式,将获得最多选票的结果作为最终的结果。后者是用串行的方式,把前一个基分类器的结果输出到下一个分类器,将所有基分类器的输出结果相加作为最终的输出。
以Adaboost为例,它基分类器的训练和合并的基本步骤如下:
训练基分类器:
合并基分类器:
另一个例子是GBDT(Gradient Boosted Decision Tree):
GBDT的基本思想是,每一棵树学的是之前所有树结论和的残差,这个残差就是一个加预测值后能得真实值的累加量。
我们以一个视频网站的用户为例,为了将广告匹配到指定年龄性别的用户,视频网站需要对每个用户的性别/年龄做出预测。在这个问题中,每个样本是一个已知性别/年龄的用户,而特征则包括这个人访问的时长、时段、观看的视频的类型等。
例如用户A的真实年龄是25岁,但第一棵决策树的预测年龄是22岁,差了3岁,即残差为3。那么在第二棵树里我们把A的年龄设为3岁去学习,如果第二棵树能把A分到3岁的叶子节点,那两棵树的结果相加就可以得到A的真实年龄;如果第二棵树的结论是5岁,则A仍然存在-2岁的残差,第三棵树里A的年龄就变成-2岁,继续学。这里使用残差继续学习,就是Gradient Boosting的意义。
2. 常用的基分类器是什么?可否将随机森林中的基分类器,由决策树替换为线性分类器或K-近邻?请解释为什么?
最常用的基分类器是决策树,这是因为:
1. 决策树可以较为方便的将样本的权重整合到训练过程中,而不需要使用过采样的方法来调整样本权重。
2. 决策树的表达能力和泛化能力,可以通过调节树的层数来做折中。
随机森林属于Bagging类的集成学习。Bagging的主要好处是集成后的分类器的方差,比基分类器的方差小。Bagging所采用的基分类器,最好是本身对样本分布较为敏感的(即所谓unstable分类器)。这样Bagging才能有用武之地。线性分类器或者K-近邻都是较为稳定的分类器,本身方差就不大,所以以它们为基分类器使用Bagging并不能在原有基分类器的基础上,获得更好的表现。甚至可能因为Bagging的采样,而导致他们在训练中更难收敛,而增大了集成分类器的偏差。
14.如何对高斯分布进行采样
场景描述
高斯分布,又称正态分布,是一个在数学、物理及工程领域都非常重要的概率分布。在实际应用中,我们经常需要对高斯分布进行采样。虽然在很多编程语言中,直接调用一个函数就可以生成高斯分布随机数,但了解其中的具体算法能够加深我们对相关概率统计知识的理解;此外,高斯分布的采样方法有多种,通过展示不同的采样方法在高斯分布上的具体操作以及性能对比,我们会对这些采样方法有更直观的印象。
问题描述
如果让你来实现一个高斯分布随机数生成器,你会怎么做?
背景知识:概率统计
解答与分析
首先,假设随机变量z服从标准正态分布N(0,1),令
x = σ·z + μ
则x服从均值为μ、方差为σ²的高斯分布N(μ, σ²)。因此,任意高斯分布都可以由标准正态分布通过拉伸和平移得到,所以这里我们只考虑标准正态分布的采样。另外,几乎所有的采样方法都是以均匀分布随机数作为基本操作,因此这里假设我们已经有均匀分布随机数生成器了。均匀分布随机数一般用线性同余法来生成(伪随机数),具体参见文献[1]。
常见的采样方法有逆变换法 (Inverse Transform Method)、拒绝采样法 (Rejection Sampling)、重要性采样及其重采样 (Importance Sampling, Sampling-Importance-Resampling)、马尔科夫蒙特卡洛采样法 (Markov Chain Monte Carlo) 等。具体到高斯分布,我们需要如何采样呢?
如果直接用逆变换法,基本操作如下:
上述逆变换法需要求解erf(x)的逆函数,这并不是一个初等函数,没有显式解,计算起来比较麻烦。为了避免这种非初等函数的求逆操作,Box-Muller算法采用如下解决方案:既然单个高斯分布的累计分布函数不好求逆,那么两个独立的高斯分布的联合分布呢?假设x,* y*是两个服从标准正态分布的独立随机变量,它们的联合概率密度为:
考虑(x,* y)在圆盘{(x, y) | x² + y*²≤ R²}上的概率:
通过极坐标变换将(x,* y)转化为(r, θ*),可以很容易求得上述二重积分:
这里F(R)可以看成是极坐标中r的累积分布函数。由于F(R)的计算公式比较简单,逆函数也很容易求得,所以可以利用逆变换法来对r进行采样;对于θ,在[0, 2π]上进行均匀采样即可。这样就得到了(r,θ),经过坐标变化即可得到符合标准正态分布的(x,* y*)。具体采样过程如下:
Box–Muller算法由于需要计算三角函数,相对来说还是比较耗时,而Marsaglia polar method则避开了三角函数的计算,因而更快,其具体采样操作如下:
除了逆变化法,我们还可以利用拒绝采样法,选择一个比较好计算累积分布逆函数的参考分布来覆盖当前正态分布(可以乘以一个常数倍),进而转化为对参考分布的采样以及对样本点的拒绝/接收操作。考虑到高斯分布的特性,这里可以用指数分布来作为参考分布。指数分布的累积分布及其逆函数都比较容易求解。由于指数分布的样本空间为x≥0,而标准正态分布的样本空间为(-∞, +∞),因此还需要利用正态分布的对称性来在半坐标轴和全坐标轴之间转化。具体来说,取λ=1的指数分布作为参考分布,
实际应用时,M需要尽可能小,这样每次的接受概率大,采样效率更高。因此,可以取
因此,具体的采样过程如下:
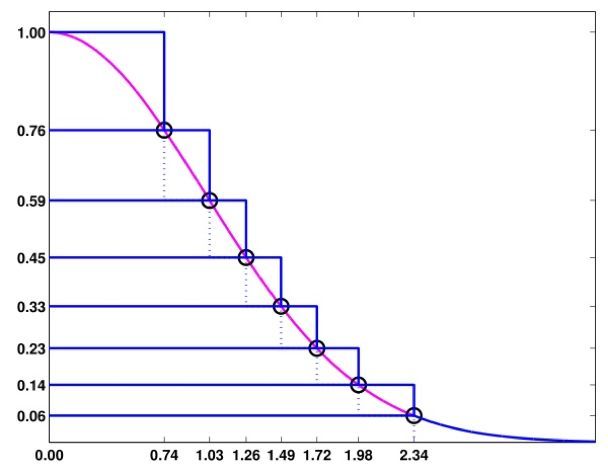
拒绝采样法的效率取决于接受概率的大小:参考分布与目标分布越接近,则采样效率越高。有没有更高效的拒绝采样算法呢?这就是Ziggurat算法,该算法本质也是拒绝采样,但采用多个阶梯矩形来逼近目标分布(如图1所示)。Ziggurat算法虽然看起来稍微繁琐,但实现起来并不复杂,操作也非常高效,其具体采样步骤可以参考文献[2]。
图1 Ziggurat算法
(图片来源于Numerical Computing with MATLAB第九章Random Numbers)
总结与扩展
高斯分布的采样方法还有很多,我们只列举了几种最常见的。具体面试时,候选人不需要回答所有的方法,知道其中一两种即可,面试官可以针对这一两种方法深入提问,如理论证明、优缺点、性能等。如果候选人没有思路,面试官可以引导其回忆那些通用的采样方法,如何将那些策略用到高斯分布这个具体案例上。另外,本题还可以适当扩展,把一般的高斯分布换成截尾高斯分布 (Truncated Gaussian Distribution) ,如何采样?如果是高维随机变量,拒绝采样法会存在什么问题?怎么解决呢?
参考文献:
[1] Linear congruential generator,
https://en.wikipedia.org/wiki/Linear_congruential_generator
[2] Ziggurat algorithm,
https://en.wikipedia.org/wiki/Ziggurat_algorithm
15. 多层感知机与布尔函数
场景描述
神经网络概念的诞生很大程度上受到了神经科学的启发。生物学研究表明,大脑皮层的感知与计算功能是通过分多层实现的,例如视觉图像,首先光信号进入大脑皮层的V1区,即初级视皮层,之后依次通过V2层,V4层,即纹外皮层,进入下颞叶参与物体识别。深度神经网络,除了其模拟人脑功能的多层结构,最大的优势在于能够以紧凑简洁的方式来表达比浅层网络更复杂的函数集合(这里的“简洁”可定义为隐层单元的数目与输入单元的数目呈多项式关系)我们的问题将从一个简单的例子引出,已知神经网络中每个节点都可以进行“逻辑与/或/非”的运算,如何构造一个多层感知机 (Multi-Layer Perceptron, MLP) 网络实现n个输入比特的奇偶校验码(任意布尔函数)?
问题描述
- 如何用多层感知机实现一个异或逻辑(仅考虑二元输入)?
- 如果只使用一个隐层,需要多少隐节点能够实现包含n元输入的任意布尔函数?
- 上面的问题中,由单隐层变为多隐层,需要多少节点?
- 合理配置后所需的最少网络层数是多少?
背景知识:数理逻辑、深度学习
解答与分析
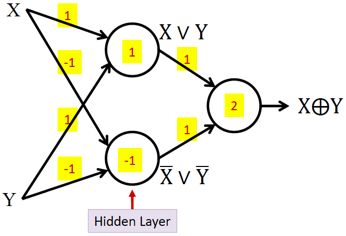
1. 如何用多层感知机实现一个异或逻辑(仅考虑二元输入)?
如下图所示(可有其他解法):
2. 如果只使用一个隐层,需要多少隐节点能够实现包含n元输入的任意布尔函数?
包含n元输入的任意布尔函数可以唯一表示为“析取范式 (Disjunctive Normal Form, DNF)”(由有限个简单合取式构成的析取式)的形式。先看一个简单的例子:
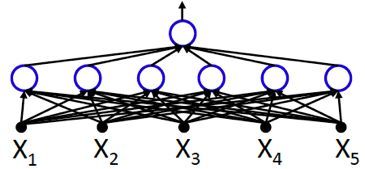
由于每个隐节点可以表示析取范式中的一个简单合取式,所以该函数可由包含六个隐节点的三层感知机实现,如下图:
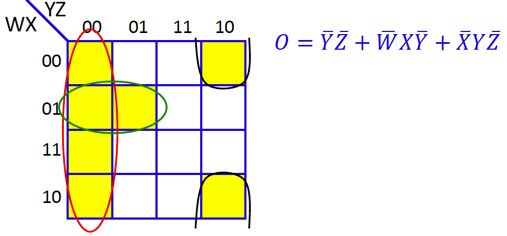
我们可以使用卡诺图表示析取式,即用网格表示真值表,当输入的合取式值为1时,则填充相应的网格。卡诺图中相邻的填色区域可以进行规约,以达到化简布尔函数的目的,如下图所示,七个填色网格最终可规约为三个合取式,故该函数可由包含三个隐节点的三层感知机实现:
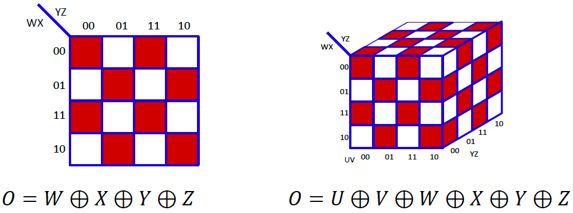
于是我们的问题可转化为,寻找“最大不可规约的”n元析取范式DNF,也等价于最大不可规约的卡诺图,直观上,我们只需间隔填充网格即可实现,其表示的布尔函数恰为n元输入的异或操作,如图:
因此,n元布尔函数的析取范式最多包含2(n-1)个合取式,对于单隐层的MLP,需要2(n-1)个隐节点可以实现。
3. 上面的问题中,由单隐层变为多隐层,构造一个n元异或函数需要多少节点?
考虑二元输入的情况,需要三个节点可完成一次异或操作;对于四元输入,包含三次异或操作,需要3×3=9个节点即可完成;而对于六元输入,包含五次异或操作,需要3×5=15个节点…依此类推,n元异或函数需要3(n-1)个节点(包括最终输出节点)。网络的构造方式可参考下图:
我们可以发现,多隐层结构可以将隐节点的数目从指数级O(2(n-1))直接减少至线性级O(3(n﹣1))!
4. 合理配置后所需的最少网络层数是多少?
根据二分思想,每层节点两两分组进行异或运算,需要两个隐层操作完成,故合理配置后需要的网络层数为2㏒2(N)。
16. 经典优化算法
场景描述
针对我们遇到的各类优化问题,研究者们提出了多种有各自适用场景的求解算法,并逐渐发展出了有严格理论支撑的研究领域——凸优化[1]。在这众多的算法中,有几种经典的优化算法是值得被牢记的,了解它们的适用场景有助于我们在面对新的优化问题时有求解思路。
问题描述
有一道无约束优化问题摆在你面前
其中目标函数 L(·) 是光滑的。请问求解该问题的优化算法有哪些?它们的适用场景是什么?
先验知识:微积分、线性代数、凸优化基本概念
解答与分析
经典的优化算法可以分为两大类:直接法和迭代法。
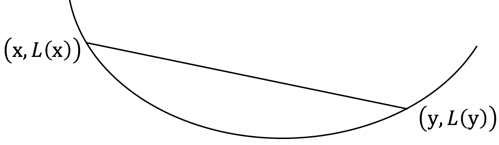
直接法,顾名思义,就是能够直接给出优化问题最优解的方法。这个方法听起来非常厉害的样子,但它不是万能的。直接法要求目标函数满足两个条件。第一个条件是,L(·)是凸函数。什么是凸函数呢?它的严格定义可以参见文献[1]的第3章:对任意x和y,任意0≤λ≤1,都成立
一个直观的解释是,任取函数曲面上的两点连接成线段,该线段的任意一点都不会处于函数曲面的下方,示意图如下
任取函数曲面上的两点连接成线段,
该线段的任意一点都不会处于函数曲面的下方
若 L(·) 是凸函数,则文献[1]第140页的一个结论是,θ是优化问题最优解的充分必要条件是 L(·) 在θ处的梯度为0,即
因此,为了能够直接求解出θ,第二个条件是,上式有闭式解。*同时满足这两个条件的经典例子是岭回归(ridge regression),其中目标函数为
稍加推导就能得到最优解为(要试着自己推导哟)
直接法的这两个要求限制了它的广泛应用,因此在很多实际问题中,我们会采用迭代法。这类方法迭代地修正对最优解的估计,即假设当前的估计为θt,我们希望求解优化问题
从而得到更好的估计θt+1=θt﹢δt。迭代法又可以分为两类,一阶法和二阶法。
一阶法对函数 L(θt﹢δ) 做一阶泰勒展开,得到近似式
由于该近似式仅在δ较小时才比较准确,我们可以求解带l2正则的近似优化问题
因此一阶法的迭代更新公式是
一阶法也称为梯度下减法,梯度是目标函数的一阶信息。
二阶法对函数 L(θt﹢δ) 做二阶泰勒展开,得到近似式
其中
是函数 L(·) 在θt处的Hessian矩阵。我们可以求解近似优化问题
从而得到二阶法的迭代更新公式
二阶法也称为牛顿法,Hessian矩阵是目标函数的二阶信息。二阶法的收敛速度一般要远快于一阶法,但是在高维情况下Hessian矩阵求逆的计算复杂度更大,而且当目标函数非凸时,二阶法有可能会收敛到鞍点(saddle point)。
扩展阅读
俄罗斯著名数学家Yurii Nesterov于1983年提出了对一阶法的加速算法[2],该算法的收敛速率能够达到一阶法收敛速率的理论界。针对二阶法矩阵求逆的计算复杂度过高的问题,Charles George Broyden,Roger Fletcher,Donald Goldfarb和David Shanno四人于1970年分别独立提出了后来被称为BFGS的伪牛顿算法[3-6],1989年扩展为低存储的L-BFGS算法[7]。
Charles George Broyden,Roger Fletcher,Donald Goldfarb和David Shanno的合影
参考文献:
[1] Boyd, Stephen, and Lieven Vandenberghe. Convex optimization. Cambridge university press, 2004.
[2] Nesterov, Yurii. "A method of solving a convex programming problem with convergence rate O (1/k2)." Soviet Mathematics Doklady. Vol. 27. No. 2. 1983.
[3] Broyden, Charles G. "The convergence of a class of double-rank minimization algorithms: 2. The new algorithm." IMA journal of applied mathematics 6.3 (1970): 222-231.
[4] Fletcher, Roger. "A new approach to variable metric algorithms." The computer journal 13.3 (1970): 317-322.
[5] Goldfarb, Donald. "A family of variable-metric methods derived by variational means." Mathematics of computation 24.109 (1970): 23-26.
[6] Shanno, David F. "Conditioning of quasi-Newton methods for function minimization." Mathematics of computation 24.111 (1970): 647-656.
[7] Liu, Dong C., and Jorge Nocedal. "On the limited memory BFGS method for large scale optimization." Mathematical programming 45.1 (1989): 503-528.