其他类型假设检验如何实现?
配对相关样本检验项目实战:如何验证统计学现象?
双独立样本检验项目实战:键盘布局A/B测试
(二)相关配对检验
斯特鲁普效应
斯特鲁普效应是当有与原有认知不同的情况出现时,人们的反应时间会较长。
实验设计
通过网上的stroop实验做测试人的反应时间(https://faculty.washington.edu/chudler/java/ready.html)。
每名参与者得到两组有颜色的文字,第一组数据是字体内容和字体颜色一致,第二组数据是字体内容和字体颜色不一致。
每名参与者对每组文字说出文字的颜色,并分别统计完成每组的时间。
此次实验共记录25组数据(样本量),并汇总到Excel表格中。
一、描述统计分析
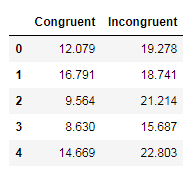
#导入包 import numpy as np import pandas as pd import matplotlib.pyplot as plt ''' 路径和文件名中不要用中文,不然会报错 encoding用于指定文件的编码,因为读取的csv中有中文,所以指定文件编码为中文编码“GBK” ''' data = pd.read_csv('斯特鲁普效应.csv') data.head()
观察数据结果:“一致”列是(第一组数据)字体内容和字体颜色一致情况下,实验者的反应时间(单位:秒)。
“不一致”列是(第二组数据)字体内容和字体颜色不一致情况下,实验者的反应时间。
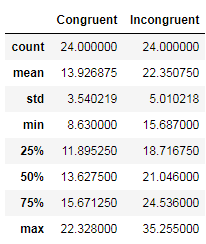
''' 第一组数据:字体内容和字体颜色一致情况下,实验者的反应时间 ''' #第一组数据均值 con1_mean = data['Congruent'].mean() # 第一组数据标准差 con1_std = data['Incongruent'].std() ''' 第一组数据:字体内容和字体颜色一致情况下,实验者的反应时间 ''' # 第二组数据均值 con2_mean = data['Incongruent'].mean() # 第二组数据标准差 con2_std = data['Incongruent'].std() #两个样本数据集对比 #画板 fg = plt.figure(figsize = (20,10)) #画纸 ax = fg.add_subplot(1,1,1) #绘制柱状图 data.plot(kind = 'bar',ax = ax) #显示图形 plt.show()
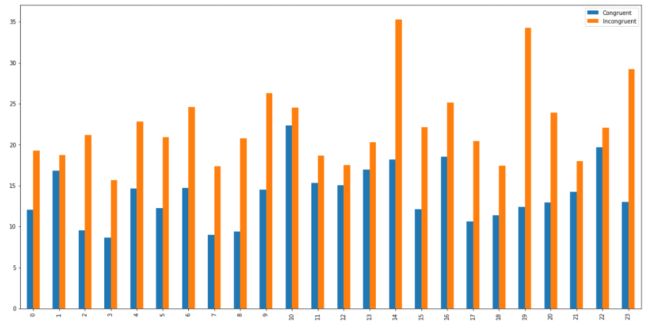
print('描述统计分析结果:') print('第一组数据:字体内容和字体颜色一致情况下,实验者的平均反应时间是:',con1_mean,'秒,标准差是',con1_std,'秒') print('第二组数据:字体内容和字体颜色不一致情况下,实验者的平均反应时间是:',con2_mean,'秒,标准差是',con2_std,'秒') print('“不一致”情况下所用时间均大于“一致”情况,也就是当字体内容和字体验证不一致时,实验者的平均反应时间变长')

二、推论统计分析
进行假设检验
1.问题是什么?
自变量是指原因。因变量是指结果,也就是自变量发生变化导致改变的值就是因变量。
自变量:我们有两组实验数据,第一组是字体内容和颜色一致。第二组数据值是字体内容和颜色不一致。所以自变量是实验数据的颜色和文字是否相同
因变量:实验者的反应时间
所以,我们要考察的是自变量(字体内容和颜色是否相同)两种情况下对因变量(反应时间)的影响。
零假设和备选假设
假设第一组“一致”的均值为 u1 ,第二组“不一致”的均值为 u2
零假设H0:人们的反应时间不会因为字体内容和字体颜色是否相同(u1 = u2 ,或者 u1-u2=0 )
备选假设H1:特鲁普效应确实存在。根据特鲁普效应的定义,颜色和文字不同的情况下,人们的完场测试的时间会变长( u1 < u2 )
检验类型
检验类型有很多种,因为该使用两组数据是相关样本,所以选择相关配对检验。
相关配对检验只关注每对相关数据的差值,从而避免得到的结论受到参与人员间正常反应时间独立性的影响。
在只关注差值集的情况下,样本集处理后只有一组(差值集)。下面我们对样本数据进行处理,从而得到差值集。
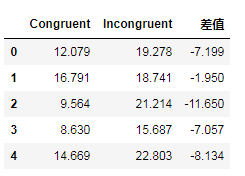
''' 获取差值数据集,也就是“一致”这一列数据,对应减去“不一致”这一列的数据 ''' #差值数据集 data['差值'] =data['Congruent'] -data['Incongruent'] data.head()
抽样分布类型
我们还要判断抽样分布是哪种?因为抽样分布的类型,决定了后面计算p值的不同。
在我们这个案例中,样本大小是25(小于30),属于小样本。那小样本的抽样分布是否满足t分布呢?
因为t分布还要求数据集近似正态分布,所以下面图片我们看下差值数据集的分布长什么样。
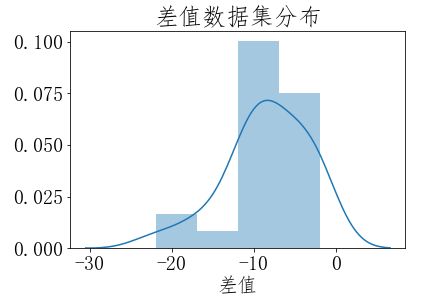
"""设置字体,用于显示中文""" plt.rcParams['font.sans-serif']=['FangSong'] """SimSun 宋体,Microsoft YaHei微软雅黑 YouYuan幼圆 FangSong仿宋""" plt.rcParams['font.size']=20 plt.rcParams['axes.unicode_minus']=False# 负号乱码 ''' 直方图能够粗略估计数据密度,如果想给数据一个更精确的拟合曲线(专业术语叫:核密度估计kernel density estimate (KDE)), Seaborn 可以很方便的画出直方图和拟合曲线。 查看数据集分布官网教程地址:https://seaborn.pydata.org/tutorial/distributions.html 安装绘图包seaborn: conda install seaborn ''' #导入绘图包 import seaborn as sns #查看数据集分布 sns.distplot(data['差值']) plt.title('差值数据集分布') plt.show()
通过观察上面差值数据集分布图,数据集近似正态分布,所以满足t分布的使用条件,我们可以使用相关样本t检验。
检验方向
单尾检验(左尾,右尾),还是双尾检验?
因为备选假设是:特鲁普效应确实存在,根据Stroop Effect的定义,颜色和文字不同的情况下,人们的完场测试的时间会变长( u1 < u2 )。
所以我们使用单尾检验中的左尾检验,显著水平为5%,t检验的自由度df=n-1=25-1=24
2.证据是什么?
在零假设成立前提下,得到样本平均值的概率p是多少?
''' 用python统计包scipy自动计算 用scipy计算出的是:双尾检验 单(1samp)样本t检验(ttest_1samp):https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_1samp.html 相关(related)配对t检验(ttest_rel):https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_rel.html 双独立(independent)样本t检验(ttest_ind):https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html ''' #导入统计模块(stats) from scipy import stats ''' ttest_rel:相关配对检验 返回的第1个值t是假设检验计算出的(t值), 第2个值p是双尾检验的p值 ''' t,p_twoTail = stats.ttest_rel(data['Congruent'],data['Incongruent']) print('t值=',t,'双尾检验的p值=',p_twoTail)
''' 因为scipy计算出的是双尾检验的t值和p值,但是我们这里是左尾检验。 根据对称性,双尾的p值是对应单尾p值的2倍 ''' #单尾检验的p值 p_oneTail=p_twoTail/2 print('单尾检验的p值=',p_oneTail)
3.判断标准是什么?
#显著水平使用alpha=5% alpha=0.05
4.做出结论
''' 因为scipy计算出的是双尾检验的t值和p值,但是我们这里是左尾检验。 根据对称性,双尾的p值是对应单尾p值的2倍 左尾判断条件:t < 0 and p/2 < alpha 右尾判断条件:t > 0 and p/2 < alpha ''' #单尾检验的p值 p_oneTail=p_twoTail/2 #显著水平 a=0.05 #决策 if(t<0 and p_oneTail< a): print('拒绝零假设,有统计显著') print('也就是接受备选假设:特鲁普效应存在') else: print('接受备选假设,没有统计显著,也就是特鲁普效应不存在')

假设检验报告:
相关配对检验t(24)=-8.35,p=7.32e-09 (α=5%),左尾检验
统计上存在显著差异,拒绝零假设,从而验证斯特鲁普效应存在。
5. 置信区间
''' 1)置信水平对应的t值(t_ci) 查t表格可以得到,95%的置信水平对应的t值=2.262 2)计算上下限 置信区间上限a=样本平均值 - t_ci ×标准误差 置信区间下限b=样本平均值 - t_ci ×标准误差 ''' ''' 95%的置信水平,自由度是n-1对应的t值 查找t表格获取, 也可以通过这个工具获取:https://www.graphpad.com/quickcalcs/statratio1/(利用这个工具获取t值,需要注意输入的概率值是1-95%=0.05) 注意:课程中这里对应的下面t_ci值有误,以下面的值为准 ''' t_ci=2.064 #差值数据集平均值 sample_mean=data['差值'].mean() #使用scipy计算标准误差 se=stats.sem(data['差值']) #置信区间上限 a=sample_mean - t_ci * se #置信区间下限 b=sample_mean + t_ci * se
6.效应量
''' 效应量:差异指标Cohen's d ''' #差值数据集对应的总体平均值是0 pop_mean=0 #差值数据集的标准差 sample_std=data['差值'].std() d=(sample_mean - pop_mean) / sample_std print('d=',d)
三、数据分析报告总结
1、描述统计分析
第一组样本数据:字体内容和字体颜色一致情况下,平均反应时间是: 13.89 秒,标准差是 3.47 秒
第二组样本数据:字体内容和字体颜色不一致情况下,平均反应时间是: 22.62 秒,标准差是 5.09 秒
“不一致”情况下所用时间均大于“一致”情况,也就是当字体内容和字体验证不一致时,实验者的平均反应时间变长
2、推论统计分析
1)假设检验
相关配对检验t(24)=-8.35,p=7.32e-09 (α=5%),左尾检验
统计上存在显著差异,拒绝零假设,从而验证斯特鲁普效应存在。
2)置信区间
两个平均值差值的置信区间,95%置信水平 CI=[-8.80,-8.67]
3)效应量
d= - 1.67