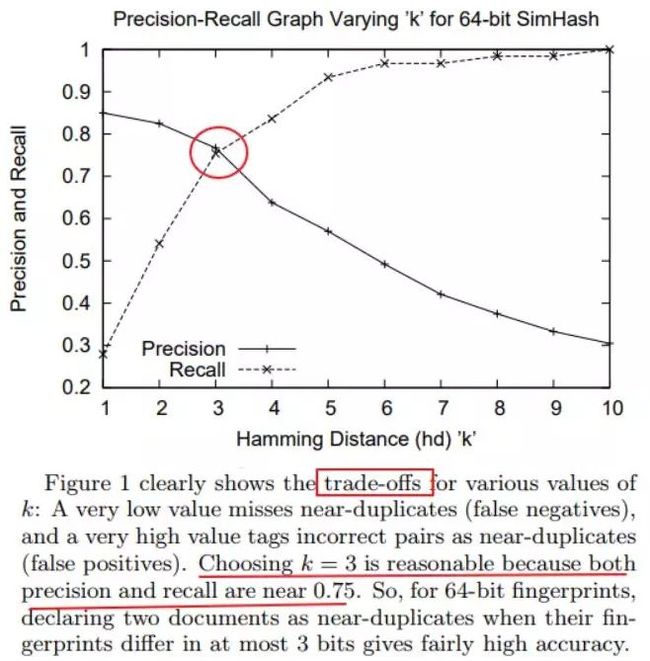
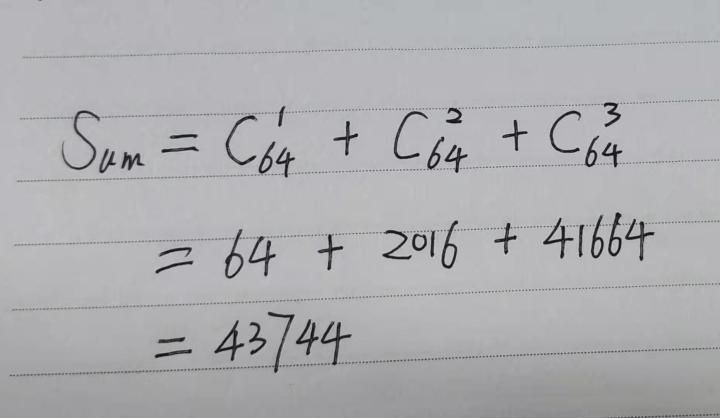题外话
最近更新文章的频率比较低，所以抓紧抽时间更新一波，要不然有人取关了，啊哈哈。
近日比较开心的一件事情是偶然的机会在开发者头条分享了一篇文章，然后这篇文章目前排在7日热度文章第二，看了下点赞近40、收藏数近200、阅读量近2w，所以更坚定了要写下去和大家一起分享学习的想法。
之前一直在系列输出Redis面试热点相关的文章，本来准备的部分还没看完无法成文，因此本次就暂且跳过了。
今天结合笔者日常工作和大家一起来学习一些偏工程的算法，都是大家很熟悉的场景，想必会有共鸣，开始今天的学习吧！
，通过本文你将了解到以下内容：
- 信息爆炸的日常生活
- 网页去重和局部敏感哈希算法
- simhash算法基本原理和过程分析
- 工程中的去重和聚类实现建议
信息爆炸
从2010年之后移动互联网如火如荼，笔者在2011年的时候还在用只能打电话发短信的那种手机，然而现在几乎每个人手机里的app起码有10-20款，以至于经常有种信息爆炸到头晕的感觉，回顾一下匆匆十年手机里的变化：
以笔者目前正在从事的信息流领域来说，有今日头条、百度App、搜狗搜索app、一点资讯、趣头条等feed软件。
很多时候都是自媒体作者会同时在多个平台发布相同的文章，然后会出现非常多的洗稿文章、抄袭文章等，我们无法杜绝和制止这种行为，但是很多时候需要我们使用技术手段来进行识别并处理，让用户看到最好的形式的文章和资讯。
信息爆炸时代，我们需要一个好的文本去重算法。
网页去重
前面是以信息流为例来说的，但是更早的文本去重场景是网页去重，像谷歌、百度、搜狗这种大型的搜索引擎，必须有一套高效的去重算法，要不然网络蜘蛛将做非常多的无用功，时效性等都无法得到保证，更重要的是用户体验也不好。
研究表明：互联网上近似重复的网页的数量占网页总数量的比例高达29%，完全相同的网页大约占网页总数量的22%。
实际中搜索引擎的去重和排序都非常复杂，本文本着简化的思路来阐述其中的一些要点，无法全面深入，对此表示歉意。
谷歌出品，必属精品，我们来看看地表最强搜索引擎是如果做网页去重呢？
这里就引出了今天要讲的主要内容simhash算法，本质上文本去重算法有很多种，每种算法都有各自的优劣势，本文并不做横向对比，而是直接引出simhash算法进行阐述，对于横向对比感兴趣的读者可以自行查阅相关资料。
局部性敏感哈希
说到hash可能我们第一个想到的是md5这种信息摘要算法，可能两篇文本只有一个标点符号的差距，但是两篇文本A和B的md5值差异就非常大，感兴趣的可以试验一下看看，Linux环境下直接md5sum即可计算。
有时候我们希望的是原本相同的文章做了微小改动之后的哈希值也是相似的，这种哈希算法称为局部敏感哈希LSH(Locality Sensitive Hashing)，这样我们就能从哈希值来推断相似的文章。
局部敏感哈希算法使得在原来空间相似的样本集合，进行相关运算映射到特定范围空间时仍然是相似的，这样还不够，还需要保证原来不相似的哈希之后仍然极大概率不相似，这种双向保证才让LSH的应用成为可能。
笔者个人认为LSH常用的用途是判重和聚类，其实这两个作用很相似，比如在信息流中我们在识别到文章相似之后无法拒绝入库，这时候就会做聚类，然后用一个id来串起来很多相似的id，从而实现相似文章的把控和管理。
simhash的基本过程
降维压缩映射
simhash算法可以将一个文本生成为一个64bit的二进制数，这里提一句simhash算法最初貌似并不是谷歌提出来的，而是谷歌应用推广的，所以本文出现的simhash相关的数据也都是基于工程中谷歌提出的simhash网页去重展开的。
谷歌2007年关于simhash的论文： https://www2007.org/papers/paper215.pdf
64bit文本容量
simhash值每个位可以是1或者0，这样就有2^64种可能了，这个有多大呢？
想必聪明的读者一定知道棋盘爆炸理论的故事：
传说西塔发明了国际象棋而使国王十分高兴，他决定要重赏西塔，西塔说：我不要你的重赏，陛下，只要你在我的棋盘上赏一些麦子就行了。
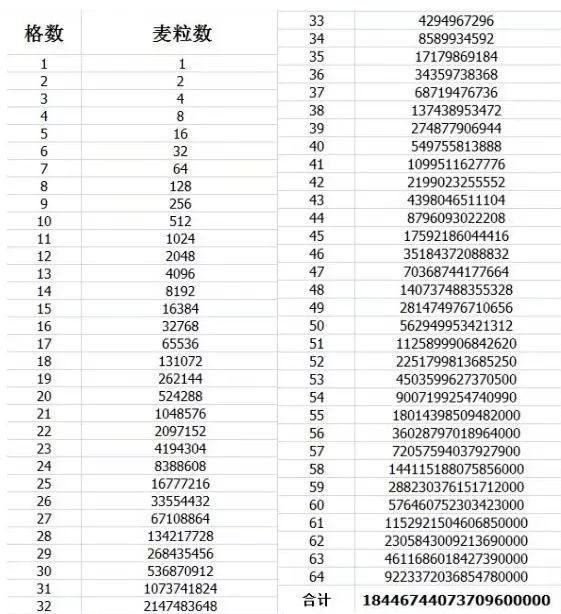
在棋盘的第1个格子里放1粒，在第2个格子里放2粒，在第3个格子里放4粒，在第4个格子里放8粒，依此类推，以后每一个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍，直到放满第64个格子就行了。
看似朴实但是如果真放满64格需要多少麦粒呢？
笔者在网上看了一些相关的资料和大家分享一下：
图片来自网络
总计需要1844.67亿亿颗麦粒，以每颗麦粒0.015g计算大约是2767亿吨，在当今粮食产量的水平下大约需要300多年才能种出来。
幂次爆炸的影响力绝非臆想所能企及的程度的，这个哥们后来不知道是不是被治了欺君之罪了，要是在我国古代那肯定悬了。
说这么多的目的是想表达simhash使用64bit的空间足够，不用有太多的担心。
哈希指纹生成过程分析
我们如何将一个文本转换为64bit数据呢？
主要步骤：在新拿到文本之后需要先进行分词，这是因为需要挑出TopN个词来表征这篇文本，并且分词的权重不一样，可以使用相应数据集的tf-idf值作为分词的权重，这样就分成了带权重的分词结果。
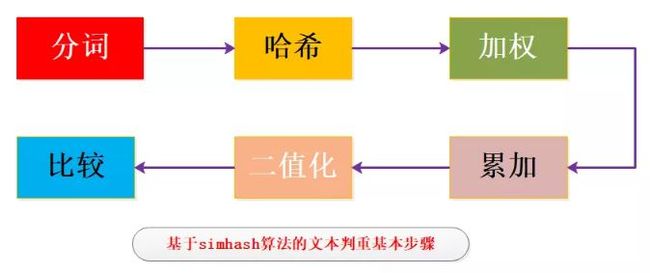
之后对所有分词进行哈希运算获取二值化的hash结果，再将权重与哈希值相乘，获得带权重的哈希值，最后进行累加以及二值化处理，先不要晕，看一张图来大致了解下：
接下来举例详细说明的判重过程，假如我们需要处理的短文本如下(本质上长文本也是一样的，相反长文本的判定比短文本更准确)：
12306出现服务器故障：车次加载失败、购买不了票或卡在候补订单支付界面等问题。官方给到消费者的建议是：卸载或重装APP，并切换网络耐心等待。
- 分词：
使用分词手段将文本分割成关键词的特征向量，分词方法有很多一般都是实词，也就是把停用词等都去掉之后的部分，使用者可以根据自己的需求选择，假设分割后的特征实词如下：
12306 服务器 故障 车次 加载失败 购买 候补订单 支付 官方 消费者 建议 卸载 重装 切换网络 耐心 等待
目前的词只是进行了分割，但是词与词含有的信息量是不一样的，比如12306 服务器 故障 这三个词就比 支付 卸载 重装更能表达文本的主旨含义，这也就是所谓信息熵的概念。
为此我们还需要设定特征词的权重，简单一点的可以使用绝对词频来表示，也就是某个关键词出现的次数，但是事实上出现次数少的所含有的信息量可能更多，这就是TF-IDF逆文档频率概念，来看下维基百科对tf-idf的解释：
tf-idf(term frequency–inverse document frequency)是一种用于信息检索与文本挖掘的常用加权技术。
tf-idf是一种统计方法，用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。
字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。
tf-idf加权的各种形式常被搜索引擎应用，作为文件与用户查询之间相关程度的度量或评级。
总之需要选择一种加权方法，否则效果会打折扣。
- 哈希计算和权重化
前面我们使用分词方法和权重分配将文本就分割成若干个带权重的实词，比如权重使用1-5的数字表示，1最低5最高，这样我们就把原文本处理成如下的样式：
12306(5) 服务器(4) 故障(4) 车次(4) 加载失败(3) 购买(2) 候补订单(4) 支付(2) 官方(2) 消费者(3) 建议(1) 卸载(3) 重装(3) 切换网络(2) 耐心(1) 等待(1)
我们对各个特征词进行二值化哈希值计算，为了简化问题这里设定哈希值长度为8bit 并非实践使用，举例如下：
12306 10011100
服务器 01110101
故障 00110011
车次 11001010
….
这样我们就把特征词都全部二值化为8bit，这里各个位的1代表+1，0代表-1，依次进行权重相乘，得到新的结果：
12306 10011100 --> 5 -5 -5 5 5 5 -5 -5
服务器 01110101 --> -4 4 4 4 -4 4 -4 4
故障 00110011 --> -4 -4 4 4 -4 -4 4 4
车次 11001010 --> 4 4 -4 -4 4 -4 4 -4
….
- 特征词带权重哈希值累加和二值化降维
经过前面的几步 我们已经将文本转换为带权重的哈希值了，接下来将所有的哈希值累加，最后将累加结果二值化，如下：
12306的带权重哈希值为5 -5 -5 5 5 5 -5 -5
服务器的带权重哈希值为-4 4 4 4 -4 4 -4 4
二者累加为 1 -1 -1 9 1 9 -9 -1
…
依次累加所有的带权重哈希值，假定最终结果为 18 9 -6 -9 22 -35 12 -5
再按照正数1负数0的规则将上述结果二值化为：11001010
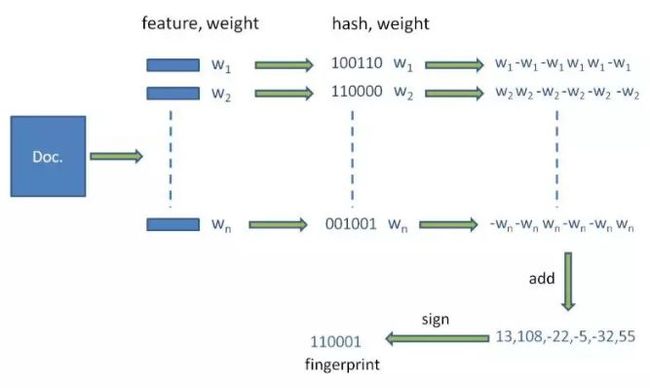
至此当收到一个新的文本时经过分词、哈希、加权、累加、二值化几个步骤就将一个文本映射到一定长度的二进制空间内，之后所有的判重和聚类操作都会基于这个降维数值进行，最后贴一张网上非常经典的图，展示一个文本进行simhash的主要步骤和细节，如图所示：
判重检索实现
前面讲述了如何生成一个文本的simhash值，接下来思考一个更重要的问题：如果对比确定相似呢？
别急，先来看看维基百科关于汉明距离的一些基础吧，后面要用到这个理论。
汉明距离
在信息论中，两个等长字符串之间的汉明距离（英语：Hamming distance）是两个字符串对应位置的不同字符的个数。换句话说，它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。
汉明重量是字符串相对于同样长度的零字符串的汉明距离，也就是说，它是字符串中非零的元素个数：对于二进制字符串来说，就是1的个数，所以11101的汉明重量是4。
对于二进制字符串a与b来说，它等于a 异或b后所得二进制字符串中“1”的个数。
汉明距离是以理查德·卫斯里·汉明的名字命名的，汉明在误差检测与校正码的基础性论文中首次引入这个概念。
在通信中累计定长二进制字中发生翻转的错误数据位，所以它也被称为信号距离。汉明重量分析在包括信息论、编码理论、密码学等领域都有应用。但是，如果要比较两个不同长度的字符串，不仅要进行替换，而且要进行插入与删除的运算，在这种场合下，通常使用更加复杂的编辑距离等算法。
理论发明者理查德·卫斯里·汉明简介
理查德·卫斯里·汉明（Richard Wesley Hamming，1915年2月11日－1998年1月7日），美国数学家，主要贡献在计算机科学和电讯。
1937年芝加哥大学学士学位毕业，1939年内布拉斯加大学硕士学位毕业，1942年伊利诺伊大学香槟分校博士学位毕业，博士论文为《一些线性微分方程边界值理论上的问题》。
二战期间在路易斯维尔大学当教授，1945年参加曼哈顿计划，负责编写计算机程序，计算物理学家所提供方程的解。该程式是判断引爆核弹会否燃烧大气层，结果是不会，于是核弹便开始试验。
1946至76年在贝尔实验室工作。他曾和约翰·怀尔德·杜奇、克劳德·艾尔伍德·香农合作。1956年他参与了IBM 650的编程语言发展工作。1976年7月23日起在美国海军研究院担当兼任教授，1997年为名誉教授。他是美国电脑协会ACM的创立人之一，曾任该组织的主席。
相关奖项和荣誉：1968年ACM图灵奖、1968年IEEE院士、1979年EmanuelR.Piore奖、1980年美国国家工程学院院士、1981年宾夕法尼亚大学Harold Pender奖、1988年IEEE理查·卫斯里·汉明奖
本文就不深究汉明距离的数学原理以及证明过程了，直接使用结论，谷歌经过工程验证认为当两个64bit的二值化simhash值的汉明距离超过3则认为不相似，所以判重问题就转换为求两个哈希值的汉明距离问题。
谷歌汉明距离的权衡
谷歌对于汉明距离的选取，笔者查询了相关论文后了解到，谷歌使用80亿的数据将汉明距离从1-10进行试验，我们可以知道当汉明距离越大意味着判重越不严格，汉明距离越小则判重更加严格，对此谷歌给出的是一个权衡值：
海量数据匹配问题
看到这里，我们又更近一步了，可以判断两个文本是否相似了，但是网页去重是面对海量数据的，我们如何对比所有数据确定相似呢？
假如库存10亿条数据的simhash值，每新来一个文本生成simhash值之后就要对库存10亿数据进行O(n)遍历吗？这个时间消耗有些大，为此我们需要进行一些工程加速，理论才能在工程中展示威力。
暴力破解思路
先看下暴力方法是如何实现的呢？
我们不知道3位以内的变化究竟会是哪些，所以这是个非精确匹配问题，计算机是无法像人一样去模糊思考的，从两个角度去分析暴力破解的情况：
- 生成64bit哈希值的3位以内的变化组合
这是个排列组合问题，相当于从64bit中挑选3bit及其以内数据作为突变点，此种情况生成组合总共有43744种组合，看个图：
- 存储时生成每个原始simhash值的所有3位内的变化组合
也就是说存储1个simhash要辅助存储43744个组合变化，空间大了4.37w倍，仿佛听到心在颤抖…
暴力破解就是典型的空间换时间，在数据量不大且不会持续增长时还好，对于海量数据无法接受，所以还得继续想办法！
一种算法优化：鸽巢原理
高中在做概率题目的时候经常有这种场景：问yyy事件的概率是多少？
一般对于这种问题正面求解的计算量会比较庞大，大的计算量也意味着出错，所以常用的套路是转换为其对立面xxx事件的概率，然后1-xxx事件的概率就是yyy的概率，然而xxx事件的概率比较好计算，采用对立迂回的战术同样解决了问题。
再看看我们的simhash相似判定的问题，之前一直关注于有至少有61位相同，现在转换为看最多有3位不同要怎么分布，或许有惊喜！
考虑一个问题：假如现在有3只鸽子，给你4个鸽子窝，每个鸽子窝可以有任意只鸽子，所以放鸽子的时候会出现什么情况呢？思考3分钟......
答案：无论怎么放最少会有1个鸽子窝是空的。
将鸽巢原理迁移到simhash相似度问题上来看，假如我们把64bit的哈希值均分为4份(鸽子窝)，那么两文本相似假如有3位不一样(3只鸽子)，那么也必然最少有一份16bit长度是完全一样的(最少有1个鸽子窝是空的)。
将鸽巢原理应用到simhash去重问题
我们在存储时将64bit哈希值平均分为4份每份16bit长，然后使用每一份作为key，value是64bit哈希值数组，原来是单个哈希值存储，彼此没有关系，现在每个哈希值都划分为4份，由整体存储转换为分散复用存储，复用的就是划分的key，从概率上来说超过2^16个数据集后必然存在key的相同数据，再贴一张笔者画的图：
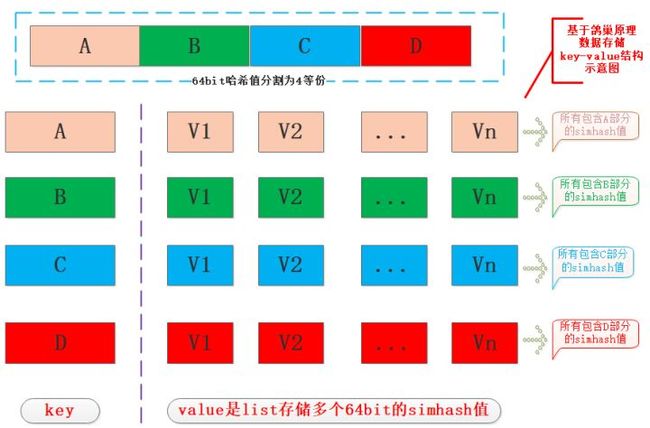注：value可以有其他形式，但是类型是个列表，因为会有很多数据的某16bit的key是一样的，对应的value中v1...vn就是其4等份中的某一份与当前key相同。
鸽巢原理应用详细说明
在图中对于一个64bit的哈希值S均分为16位长度四个部分ABCD，在存储时分别以ABCD为key进行存储，如果当前key已经存在，那么就将S追加到key对应的value列表中，也就是说value中存储的都是四等份中存在key的哈希值。
当新来一个文本生成哈希值S'之后，按照相同的规则生成abcd四部分，之后逐个进行哈希对比，这个时间复杂度是O(1)：
- 如果abcd四个作为key都不存在，那么可以认为S'没有相似的文本；
- 如果abcd四个key中有命中，那么就开始遍历对应key的value，查看是否满足<=3的汉明距离确定相似性；
- 如果上一个命中的key未找到相似文本，则继续遍历剩下的key，重复相同的过程，直至所有的key全部遍历完或者命中相似文本，则结束。
以库存10亿数据为例复杂度分析
10亿数据大约是2^30，key的长度为16bit，由于数据量比较大所以理论上key分布均匀，存储中约有2^16(65536)个key，肯定不会多于65536的。
每个key对应value的list长度最大是(2^14)*4=65546个，因为key在哈希值中的位置可能是1/2/3/4，这样理论上第1位是key的数量是2^30/2^16=2^14，同理第2/3/4位置上也是这样的，所以value最大长度是(2^14)*4。
最坏情况待匹配哈数值S'的四个key，ABCD均命中了但是依次遍历之后都相似度判断失败了，这种情况的理论最大匹配次数是4*65536=262144次。
犯嘀咕
写到这里笔者心里有点犯嘀咕，因为网上虽然有些介绍simhash的但是有的计算存和存储的思路也有一些差异，工程使用中设计方案也不同，因此上述的计算主要表达了从亿级降低到万级的优化思想。
水平所限笔者现在的思路可能存在问题或者不是最优解，如果有读者发现问题，可以私信我哈！
一些工程实践优化
前面重点阐述了simhash的原理和网页去重应用过程，结合笔者自身在做信息流文章判重和聚类的相关经验来看，很多新闻类文章的时效性区分比较明显，也就是2019年12月20号的文章跟2018年12月20号的文章相似的概率很低，这种场景下存储海量数据可能产生浪费，因为大部分数据都是不相似的，所以在实际使用中旨在理解simhash的核心思想，然后采用适合自己的判重和聚类算法。
一般来说进行判重和聚类离不开分词，在实践中笔者使用JieBa分词的C++版本封装了一个分词服务，支持批量和多种分词方式，不过结巴的词库貌似是使用人民日报的语料训练的tf-idf，并不适用所有场景，所以我们采用自己的数千万文章数据建立了自己的tf-idf表，实际效果比默认的tf-idf好一些。
没有万能的方法 只有万能的思想。
掌握核心要点就可以自己展开设计调整，效果不一定比网上那些成功范例差甚至更好，这也是学习和实践的乐趣吧！