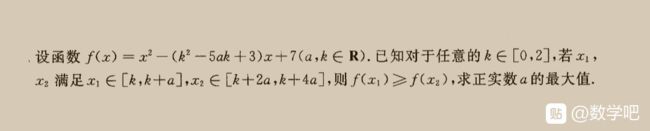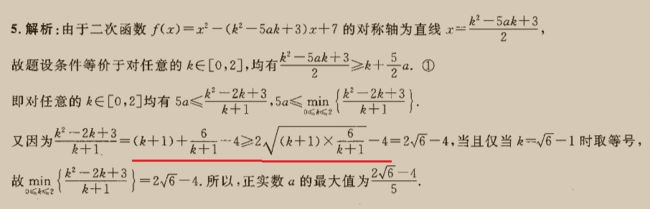有 网友 在 数学吧 里 发了一个 帖 《没什么思路,帮解答下,谢谢》 http://tieba.baidu.com/p/6463688651 ,
里面 提出了 一个 题,
以下 是 在 帖 里 的 回复 :
4 楼
可以先看一下 当 x1 >= x2 >= 0 时, f(x1) 和 f(x2 ) 的 大小关系,
可以知道, 当 x1 >= x2 >= 0 时,
f(x1) - f(x2) = e^x1 + x1² - (e^x2 + x2²) = e^x1 - e^x2 + x1² - x2² >= 0 ,
f(x1) >= f(x2)
再看一下 当 x1, x2 < 0 时, f(x1) 和 f(x2 ) 的 大小关系,
f(x1) - f(x2) = e^(-x1) + x1² - ( e^(-x2) + x2² ) = e^(-x1) - e^(-x2) + x1² - x2² ,
因为 x1, x2 < 0 ,可以知道, 若 x1 >= x2, f(x1) - f(x2) <= 0 , f(x1) <= f(x2)
所以, 当 x1, x2 >= 0 时, 若 x1 >= x2 , f(x1) >= f(x2) ,
当 x1 , x2 < 0 时, 若 x1 <= x2 , f(x1) >= f(x2) ,
我们再来看看 a 、k 能够 让 x1, x2 的 值 位于 什么大小范围 , 可以看出来, ABCD 4 个 答案选项 中 的 k 都会让 x1 存在 小于 0 的 情况, ABC 3 个选项 会让 x2 有 大于 0 的 情况, 只有 D 选项 使得 x1, x2 总是 小于 0, 且 x1 < x2, 此时 f(x1) >= f(x2) , 所以 D 选项 是 满足条件 的 选项, 选 D 。
花月弄碎乱蝶玉: 谢谢,但我想知道下k具体是怎么算取值的。
花月弄碎乱蝶玉: 在吗?
花月弄碎乱蝶玉: 我有一道相似的题目,但没看懂。你可以看看吗?在下面。
K歌之王: 回复 花月弄碎乱蝶玉 :比如 可以把 a = 根号 3 和 k = 4 代入,此时, a - k / a < 0 , 但是 a - k / 3a > 0 , 而 a - k / a , a 越小, k 越大, 越可能 负, a - k / 2a , a - k / 3a , a - k / 4a 亦然 。
K歌之王: 回复 花月弄碎乱蝶玉 :a - k / 2a 比 a - k / a < 0 更不容易负, a - k / 3a 比 a - k / 2a 更不容易负, a - k / 4a 比 a - k / 3a 更不容易负, 所以 要让 全部 都 负, 需要 k 比较 大, 只有 D 选项 满足 。
花月弄碎乱蝶玉: 我了解,我只是想单号解答题一样解出k的取值。
5 楼
花月弄碎乱蝶玉 :
第二步不知道怎么来的
MATHS40: 第二步可用单调性做
花月弄碎乱蝶玉: 如何得到>k+5/2a呢
花月弄碎乱蝶玉: 在吗
花月弄碎乱蝶玉: 会了,谢谢
6 楼
回复 4 楼 “想单号解答题一样解出k的取值” , 哦 ~~, 我分了 三个 情况来看, 就是
x1, x2 >= 0 , x1, x2 < 0 , x1, x2 有 大于 0 也有 小于 0 ,
如果 题目 可以 归到 x1, x2 >= 0 或者 x1, x2 < 0 , 就比较简单, 实际上 确实可以 归 到 x1, x2 < 0 , 所以 就 朝 这个 方向 来 看 。
如果 是 看 普遍 的 x1, x2 有 大于 0 也有 小于 0 的 情况 来 解出 k 的 范围, 因为是 分段函数, 可能 要 考虑 4 种 情况, 列 4 个 方程, 这些方程 里 含有 e^x 和 x² , 这种方程 似乎 不好解, 觉得 出题人 的 方向 应该 不是 这个 方向 吧 ,,, 哈哈 。
这种 情况 比较 复杂, 4 个 选项 中 大概 很难 有 满足 条件 的 。
7 楼
第二步 是指 红线 划 的 那个 不等式 吗?
那是一个 公式 a + b >= 2 根号 (a b) , a >= 0, b>= 0
可以由 平方和 公式 得到: ( 根号 a - 根号 b ) ² >= 0
a - 2 根号 ( a b ) + b >= 0
a + b >= 2 根号 ( a b )
花月弄碎乱蝶玉: 是第二行。
花月弄碎乱蝶玉: 是k+5/2a
花月弄碎乱蝶玉: 在吗,均值不等式我还是知道的。。。
花月弄碎乱蝶玉: 两题都想懂了,一样的,原题是偶函数,对称轴x=0,只要a≤3k/8a就行。这个是二次函数对称轴,k+5/2a≤对称轴就行。
K歌之王: 回复 花月弄碎乱蝶玉 :我前几天才知道 均值不等式, 就想那里去了 。。。
9 楼
J唐奈儿 :
求试卷
花月弄碎乱蝶玉: 2019浙江高考模拟三。如果要做的话,可以看看第17题,那个答案长轴比短轴短,感觉很奇怪,可能是我想错了。。