本文发布于游戏程序员刘宇的个人博客, 转载请注明来源https://www.cnblogs.com/xiaohutu/p/10950011.html
某天我在优化游戏的算法,在将一个个关键数据结构优化全部成位操作后,最终来到最后一座大山前,如何快速计算出这个数值的二进制表示中最后一位的1在哪一位?
首先,我们已知:
将二进制只保留最后一位1的算法:
v & -v 的原理
已知IEEE对有符号整数中负数的定义是所有数值位取反+1,首位填1,首位这样正负数加起来既可以为0。
例如:一个8位的整数
A = 0001 1000, 取反 0110 0111, 取反加1 0110 1000,首位填1得到 -A = 1110 1000
A + -A 正好加到最高一位进位后为 0000 0000
因为取反的时候加1,所以A最后一个为1的位取反后为0,下面我们称为第N位
取反后的第N位为0,后面全为1,再加1后的数值上第N位变成1,后面全为0
此时A和-A里,第N位之后的位全为0,第N位之前的位全为反
所以两个数进行与操作,只有第N位为1
即: 0001 1000 & 1110 1000 = 0000 1000
那么,如何将v&-v转换成N呢?
德布莱英序列
我看到了一段代码:
unsigned int v;
int r;
static const int MultiplyDeBruijnBitPosition[32] =
{
0, 1, 28, 2, 29, 14, 24, 3, 30, 22, 20, 15, 25, 17, 4, 8,
31, 27, 13, 23, 21, 19, 16, 7, 26, 12, 18, 6, 11, 5, 10, 9
};
r = MultiplyDeBruijnBitPosition[((uint32_t)((v & -v) * 0x077CB531U)) >> 27];
计算过程可以理解为:
将0x077CB531U的二进制:
00000111011111001011010100110001
乘以 v&-v,即左移N位,再右移27位,得到的常数在MultiplyDeBruijnBitPosition里查表,得到的结果即是N。
例如乘以 100 0000,(6个0,左移6位)
00000111011111001011010100110001
-> 11011111001011010100110001000000
再右移27位
-> 11011
得到的数字是27,在数组里是6
很神奇,不是吗?
仔细分析一下这个数字,可以发现,这个数字从每一位分别开始看,连续5位(到结尾循环),是所有5位的二进制数字的全集,而且左移28-31位时,结尾填0,正好序列开始的几个数字也是0。
那么不难理解,从这个数列的第X位任意取5位,都可以得到一个0-31的数字,并且根据查表取出这个数字对应是左移过几位。
为什么会存在这样的序列
把二进制依次写出,如果是两位,我们让每个两位数字的最后一位等于下一个两位数字的第一位, 00-01-11-10,写出 0011,长度为4。
三位,我们让每个三个数字的后两位等于下一个数字前两位,001-011-111-110-101-010-000,写出00111010,长度为8。
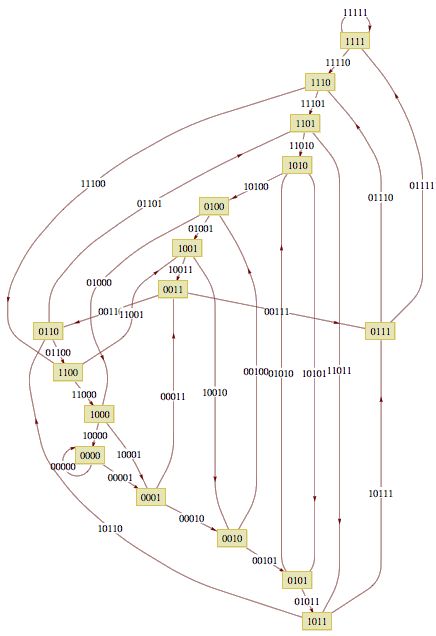
四位,见图:
依此类推,到第N位,我们可以让每个数的后N-1位等于下一个数字的前N-1位,得到长度为 2的N次方长度的2进制序列。
这就是德布莱英原理:一定存在长度为2的N次方长度的二进制串,循环来看,一位位移动,可以完整描述所有N位长度的二进制数字的集合。
链接1:https://en.wikipedia.org/wiki/De_Bruijn_sequence
链接2:https://baike.baidu.com/item/德布莱英序列/18898516?fr=aladdin
我们可以任意生成这样的序列吗
稍微经过研究可以发现,Debrujin序列是密码学中运用很广泛的序列,已知原理,可以编程来实现自动求序列的代码。
1. 暴力遍历
2. 递归法 https://blog.csdn.net/lusongno1/article/details/51104737
3. 本原多项式方法 https://blog.csdn.net/sea_sky_cloud/article/details/80932402