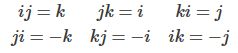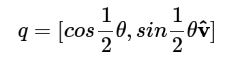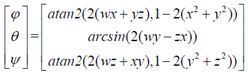本文发布于游戏程序员刘宇的个人博客,长期更新,转载请注明源地址https://www.cnblogs.com/xiaohutu/p/10979936.html
数学,是人类对客观世界中数量关系和空间形式本质特征进行研究的科学。对同样的某一特征或者关系,可以根据需求用不同的数学符号、定义和过程来表达。在游戏引擎中,我们也有很多这样的例子,比如本文说到的旋转。
欧拉角
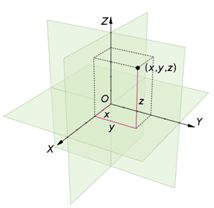
旋转是一个过程,一个物体围绕周或者点角度变化的过程。为了描述这个过程我们必须有参照物,于是我们先定义一个世界坐标系,笛卡尔坐标系。
欧拉角用(x, y, z) 分别来表示这个物体相对三个坐标系的夹角,这是由数学家欧拉首先提出而得名的。
然而仅仅有(x, y, z) 来表示旋转是不够的,还有两个因素:
首先是旋转顺序,从各个轴上进行角度旋转时xyz先后的不同会得到不同的结果。我们称这个顺序定义为顺规,下面一段是维基百科的定义:
在经典力学里,时常用zxz顺规来设定欧拉角;照着第二个转动轴的轴名,简称为x顺规。另外,还有别的欧拉角组。合法的欧拉角组中,唯一的限制是,任何两个连续的旋转,必须绕着不同的转动轴旋转。因此,一共有12种顺规。例如,y顺规,第二个转动轴是y-轴,时常用在量子力学、核子物理学、粒子物理学。另外,还有一种顺规,xyz顺规,是用在航空航天工程学;
按(z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)轴序列旋转,即第一个旋转轴和最后一个旋转轴相同,我们称之为经典欧拉角(Proper Euler Angle)。
按(x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z)轴序列旋转,即三个不同的轴,我们称之为泰特布莱恩角(Tait–Bryan angles)。
其次是旋转的参照坐标系,欧拉角按旋转的坐标系分为:
内旋(intrinsic rotation)即按照物体本身的坐标系进行旋转,坐标系会跟随旋转与世界坐标系产生偏移。
外旋(extrinsic rotation)即根据世界坐标系进行旋转。
这是我们看看Unity3d中Transform的Rotate,最后一个参数即坐标系:
public void Rotate(Vector3 eulerAngles, Space relativeTo = Space.Self);
注意:Unity3d使用的是zxy的顺规,且进行一次欧拉旋转的zxy依次执行过程中,相对轴始终是运算开始之前的轴向。
万向节死锁(Gimbal Lock)
注意我们前面提到的旋转的规则 [ 进行一次欧拉旋转的zxy依次执行过程中,相对轴始终是运算开始之前的轴向 ]
在这个规则下,zxy顺规时,如果x的旋转为90度,那么任意的(z,90,y)都与(z-y,90,0)得到的结果都是相同的,此时我们称z轴失去了自由度,并称这种情况为万向节死锁。之所以叫Gimbal Lock,是因为这种情况正好和Gimbal,即陀螺仪的情况是完美匹配的,死锁情况也相同。具体情况这篇文章写的很好,大家可以看一下:https://blog.csdn.net/andrewfan/article/details/60981437
这种情况下,物体的某一个旋转,会有多个欧拉角数值与其多对一的对应,那么对欧拉角进行插值是没有意义的。如果只旋转一个轴,其他轴不动,那么直接设置欧拉角的数值倒是没有什么问题。
同时我们也不难得出死锁的原因并不是由顺规决定的,而是由于欧拉角的原理和计算方式,一个轴的旋转必然带来另外轴的旋转所导致的。
轴向角
这时候,又有了一个思路,我们可以使用基于一个单位矢量来表示方向,再用一个标量来定义绕这个矢量来旋转多少角度theta。
即[x,y,z,theta],前面的xyz表示这个矢量,最后一个表示角度。这个表示方法很简洁明了,容易理解。
缺点有两个:
1.不同的轴角之间不能进行简单的插值。
2.不好基于一个矢量加上一个轴角形式的旋转来进行运算。
为了解决这些缺点,先人们又发明了使用四元数和矩阵来表达旋转。
四元数
这里先说一下基本原理:
参考链接:https://www.3dgep.com/understanding-quaternions/
译文:https://blog.csdn.net/lhs322/article/details/80066960
四元数的概念是由爱尔兰数学家汉密尔顿发明的,他当时正和老婆一起前往爱尔兰皇家研究院,一边走一边想,路过一座桥时,他顿悟了公式,并立刻把它刻在桥上的石头上:
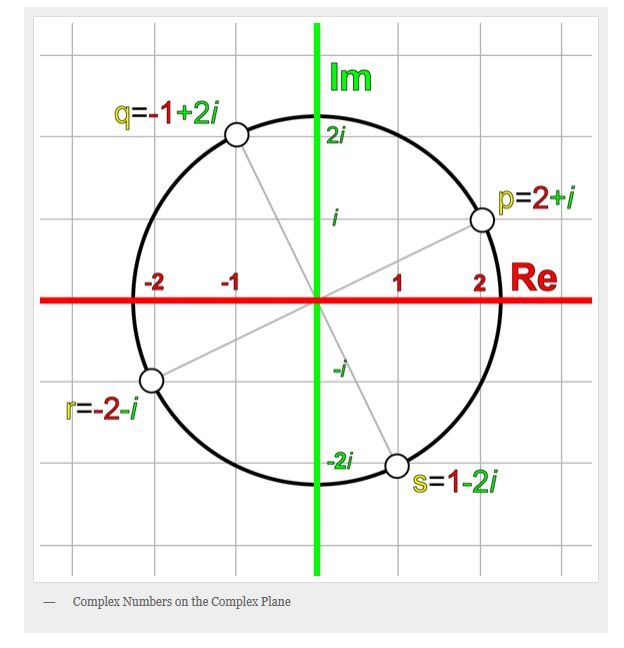
那么,为什么四元数能表示三维空间的旋转呢?首先学过高数我们都知道复数的定义以及几何意义,复数可以映射到复数平面上,并且对这复数乘以i,得到的复数就相当于复数空间里旋转了90度。
例如下图,p = 2 + i,乘以i后: q = pi = (2+i)*i = 2i + i*i = 2i - 1 = -1 + 2i。可以看出q逆时针旋转了90度。同理乘以-i即为正时针旋转90度。
此时将复数的虚部扩展为三个,并根据汉密尔顿的著名表达式以及推论
![]()
四元数的定义可以用来表达笛卡尔坐标系的旋转,其中i,j,k分别代表笛卡尔坐标系里xyz三个轴的单位向量。这些表达式里 ij = k 是不是很眼熟?两个互相垂直的单位向量的叉乘等于垂直于两个向量的单位向量。
经过一系列的推导和运算(略),大家感兴趣可以看上面的链接,假设一个旋转的基准向量![]() 是(A,B,C),角度是 θ (theta),那么表达这个旋转过程的四元数如下:
是(A,B,C),角度是 θ (theta),那么表达这个旋转过程的四元数如下:
注意ABC本质上就是基准向量![]() 在3个笛卡尔轴上的分量,用来准确描述向量
在3个笛卡尔轴上的分量,用来准确描述向量![]() ,上面的公式也就是
,上面的公式也就是
四元数 q = [cos(θ/2), sin(θ/2)* v‘];
即:
w = cos(θ/2) x = A * sin(θ/2) y = B * sin(θ/2) z = C * sin(θ/2)
假设有一个向量v要进行旋转,这个旋转描述为q,那么结果是 v' = qvq-1, 如果要进行多次旋转,则表示为:
![]()
四元数的乘法是:
q1 * q2 =
(w1*w2 - x1*x2 - y1*y2 - z1*z2) +
(w1*x2 + x1*w2 + y1*z2 - z1*y2) i +
(w1*y2 - x1*z2 + y1*w2 + z1*x2) j +
(w1*z2 + x1*y2 - y1*x2 + z1*w2) k
可以看到,通过一系列的数学推导和定义,可以只用4个浮点数就来表达一个旋转过程,并且可以方便简单的快速计算旋转的叠加。这对于游戏引擎来说是非常有意义的,可以加快运算速度。
四元数还有很多具体的特性,计算规则等,感兴趣的可以去研究,本文主要讨论旋转,这里不再赘诉。
【球形插值】
四元数还可以实现球形插值,制定两个旋转qa到qb,时间间隔为t,那么此刻的旋转插值为:
![]()
其中θ为两个旋转之间的夹角:
![]()
球面插值可以在游戏里实现很平滑的转向和球面运动。
四元数与欧拉角之间的转换
已知欧拉角,求四元数:
已知四元素,求欧拉角
用矩阵来计算旋转
学过矩阵乘法我们都知道,如果把向量看成一个列矩阵,那么与向量维度相同的列数的矩阵乘以它,得到的结果也是一个列矩阵,即:
所以可以充分利用左边矩阵的内容,对右边的向量进行各种变换(包括平移,缩放,旋转等等),这里我们只讨论旋转。
具体推导过程参考这里:https://www.cnblogs.com/xpvincent/archive/2013/02/15/2912836.html
假设一个向量V(Vx,Vy, Vz) 绕另外一个轴角(nx, ny, nz, θ)进行旋转,那么旋转结果V'是:
这个公式我们称之为罗德里格旋转公式(Rodrigues' rotation formula),用矩阵计算旋转在游戏图形渲染里非常普遍,不过引擎里一般为了兼容更多的向量变换,都使用了其次矩阵,即多一个维度的矩阵,本文不表。
小结
总结完这几种在常见的表达旋转的数学方式,可以看到游戏引擎里也都使用到这些表达方法,感觉收益匪浅,后面准备讨论一下齐次矩阵和矩阵变换的原理。