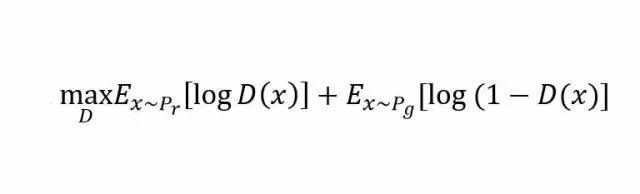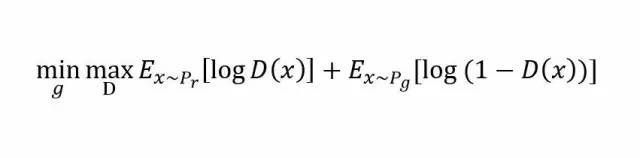GAN生成对抗网络从入门到实践——入门级

自2014年Ian Goodfellow提出生成对抗网络(GAN)的概念后,生成对抗网络变成为了学术界的一个火热的研究热点，Yann LeCun更是称之为”过去十年间机器学习领域最让人激动的点子”.

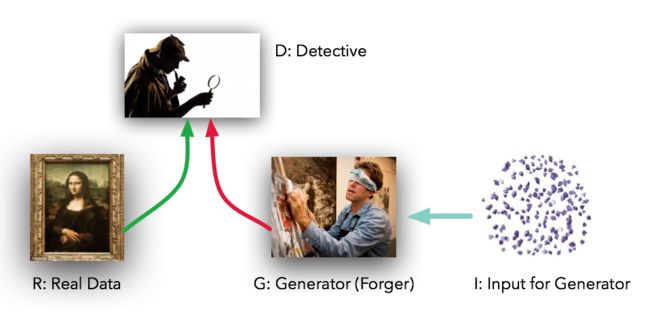
生成对抗网络包括一个生成器(Generator,简称G)生成数据，一个鉴别器(Discriminator,简称D)来鉴别真实数据和生成数据,两者同时训练,直到达到一个纳什均衡，生成器生成的数据与真实样本无差别，鉴别器也无法正确的区分生成数据和真实数据.

0.入门姿势——生成模型

生成模型故名思议就是已知模型，用来生成适应该模型的数据，那么它有什么应用场景呢？

主要的应用场景有两种：

1. 当我们拥有大量的数据，例如图像、语音、文本等，如果生成模型可以帮助我们模拟这些高维数据的分布，那么对很多应用将大有裨益。

2. 针对数据量缺乏的场景，生成模型则可以帮助生成数据，提高数据数量，从而利用半监督学习提升学习效率。语言模型（language model）是生成模型被广泛使用的例子之一，通过合理建模，语言模型不仅可以帮助生成语言通顺的句子，还在机器翻译、聊天对话等研究领域有着广泛的辅助应用。

那么，如果有数据集S={x1，…xn}，如何建立一个关于这个类型数据的生成模型呢？

最简单的方法就是：假设这些数据的分布P{X}服从g(x;θ)，在观测数据上通过最大化似然函数得到θ的值，即最大似然法。

例如，我们知道一一些文本中有若干单词，我们就可以用单词出现的频率作为这些数据的分布（如单词“text”的概率0.3，“today”的概率为0.1），以这些概率来生成新的文档。

GAN也是一种生成模型，不过是一种以于半监督学习方式训练的模型，基于神经网络，经常被用在图像处理和半监督学习领域。

1.基本原理

GAN有一个生成器(Generator,简称G)生成数据，一个鉴别器(Discriminator,简称D)鉴别数据是否与真实数据相似。

生成模型

鉴别器的作用G：尽最大努力区分生成器生成的数据和真实数据

生成器作用D：生成和真实数据几乎没有差距的数据

上述的博弈过程就基本上是GAN的原理了。

那么GAN的数学形式是怎样的呢？

假设我们的生成模型是g(z)，其中z是一个随机噪声，而g将这个随机噪声转化为数据类型x，仍拿图片问题举例，这里g的输出就是一张图片。D是一个判别模型，对任何输入x，D(x)的输出是0-1范围内的一个实数，用来判断这个图片是一个真实图片的概率是多大。令Pr和Pg分别代表真实图像的分布与生成图像的分布.

鉴别器的作用效果：

鉴别器D

生成器的作用效果：

生成器G

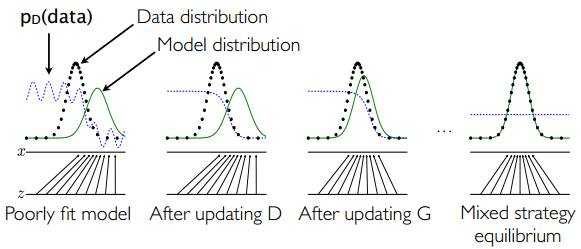
整体效果大概是下面这样：

迭代过程

图中黑色虚线是真实数据的高斯分布，绿色的线是生成网络学习到的伪造分布，蓝色的线是判别网络判定为真实图片的概率，标x的横线代表服从高斯分布x的采样空间，标z的横线代表服从均匀分布z的采样空间。可以看出G就是学习了从z的空间到x的空间的映射关系。

2.GAN优缺点及改进

2.1GAN的优劣势

优势

• GANs是一种以半监督方式训练分类器的方法,可以参考我们的NIPS paper和相应代码.在你没有很多带标签的训练集的时候,你可以不做任何修改的直接使用我们的代码,通常这是因为你没有太多标记样本.我最近也成功的使用这份代码与谷歌大脑部门在深度学习的隐私方面合写了一篇论文
• GANs可以比完全明显的信念网络(NADE,PixelRNN,WaveNet等)更快的产生样本,因为它不需要在采样序列生成不同的数据.
• GANs不需要蒙特卡洛估计来训练网络,人们经常抱怨GANs训练不稳定,很难训练,但是他们比训练依赖于蒙特卡洛估计和对数配分函数的玻尔兹曼机简单多了.因为蒙特卡洛方法在高维空间中效果不好,玻尔兹曼机从来没有拓展到像ImgeNet任务中.GANs起码在ImageNet上训练后可以学习去画一些以假乱真的狗
• 相比于变分自编码器, GANs没有引入任何决定性偏置( deterministic bias),变分方法引入决定性偏置,因为他们优化对数似然的下界,而不是似然度本身,这看起来导致了VAEs生成的实例比GANs更模糊.
• 相比非线性ICA(NICE, Real NVE等,),GANs不要求生成器输入的潜在变量有任何特定的维度或者要求生成器是可逆的.
• 相比玻尔兹曼机和GSNs,GANs生成实例的过程只需要模型运行一次,而不是以马尔科夫链的形式迭代很多次.

劣势

• 训练GAN需要达到纳什均衡,有时候可以用梯度下降法做到,有时候做不到.我们还没有找到很好的达到纳什均衡的方法,所以训练GAN相比VAE或者PixelRNN是不稳定的,但我认为在实践中它还是比训练玻尔兹曼机稳定的多.
• 它很难去学习生成离散的数据,就像文本
• 相比玻尔兹曼机,GANs很难根据一个像素值去猜测另外一个像素值,GANs天生就是做一件事的,那就是一次产生所有像素, 你可以用BiGAN来修正这个特性,它能让你像使用玻尔兹曼机一样去使用Gibbs采样来猜测缺失值,

以上是GAN的发明者者回答网友问

2.2 GAN的改进

常见的改进深度卷积的对抗生成网络（DC-GAN），在图像中有着很重要的应用

在图像生成过程中，如何设计生成模型和判别模型呢？深度学习里，对图像分类建模，刻画图像不同层次，抽象信息表达的最有效的模型是：CNN （convolutional neural network，卷积神经网络）。

在CSDN上看到一个例子，会发现DC-GAN的优化效果会好很多

DC-GAN优化

3.实践

我们需要准备以下的东西：

1. R：原始的真实数据
   我们使用一个贝尔分布作为真实的数据，贝尔分布需要提供一个均值和标准差，代码中选择均值和标准差分别为0.4和1.25

# ##### DATA: Target data and generator input data

def get_distribution_sampler(mu, sigma):
    return lambda n: torch.Tensor(np.random.normal(mu, sigma, (1, n)))  # Gaussian

2. I：一个原始的噪声，为生成器提供数据的来源
   对生成器的输入也是随机的，这是要使我们的工作变得困难一点，让我们使用一个连续型均匀分布，而不是一个正态分布。这意味着我们的模型 G 不能简单地转移/缩放输入数据来达到 R的效果，必须以非线性的方式重新调整数据。

def get_generator_input_sampler():
    return lambda m, n: torch.rand(m, n)  # Uniform-dist data into generator, _NOT_ Gaussian

3. G：生成器——努力让数据模仿真实数据

# ##### MODELS: Generator model and discriminator model

class Generator(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Generator, self).__init__()
        self.map1 = nn.Linear(input_size, hidden_size)
        self.map2 = nn.Linear(hidden_size, hidden_size)
        self.map3 = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        x = F.elu(self.map1(x))
        x = F.sigmoid(self.map2(x))
        return self.map3(x)

4. D：判别器——努力区分真实数据和生成的数据

class Discriminator(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Discriminator, self).__init__()
        self.map1 = nn.Linear(input_size, hidden_size)
        self.map2 = nn.Linear(hidden_size, hidden_size)
        self.map3 = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        x = F.elu(self.map1(x))
        x = F.elu(self.map2(x))
        return F.sigmoid(self.map3(x))

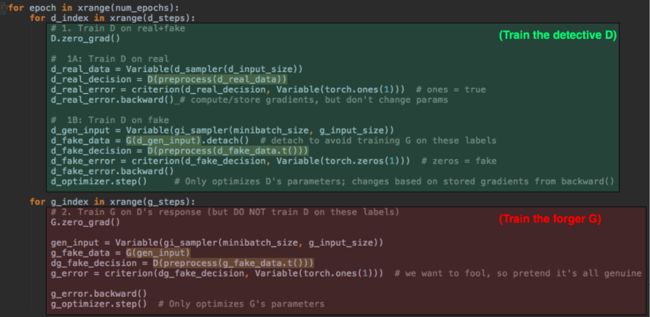
5. 一个用来训练的循环——让G和D对抗

   
   
   

   训练网络

完整代码

# Generative Adversarial Networks (GAN) example in PyTorch.
# See related blog post at https://medium.com/@devnag/generative-adversarial-networks-gans-in-50-lines-of-code-pytorch-e81b79659e3f#.sch4xgsa9
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.autograd import Variable

# Data params
data_mean = 4
data_stddev = 1.25

# Model params
g_input_size = 1     # Random noise dimension coming into generator, per output vector
g_hidden_size = 50   # Generator complexity
g_output_size = 1    # size of generated output vector
d_input_size = 100   # Minibatch size - cardinality of distributions
d_hidden_size = 50   # Discriminator complexity
d_output_size = 1    # Single dimension for 'real' vs. 'fake'
minibatch_size = d_input_size

d_learning_rate = 2e-4  # 2e-4
g_learning_rate = 2e-4
optim_betas = (0.9, 0.999)
num_epochs = 30000
print_interval = 200
d_steps = 1  # 'k' steps in the original GAN paper. Can put the discriminator on higher training freq than generator
g_steps = 1

# ### Uncomment only one of these
#(name, preprocess, d_input_func) = ("Raw data", lambda data: data, lambda x: x)
(name, preprocess, d_input_func) = ("Data and variances", lambda data: decorate_with_diffs(data, 2.0), lambda x: x * 2)

print("Using data [%s]" % (name))

# ##### DATA: Target data and generator input data

def get_distribution_sampler(mu, sigma):
    return lambda n: torch.Tensor(np.random.normal(mu, sigma, (1, n)))  # Gaussian

def get_generator_input_sampler():
    return lambda m, n: torch.rand(m, n)  # Uniform-dist data into generator, _NOT_ Gaussian
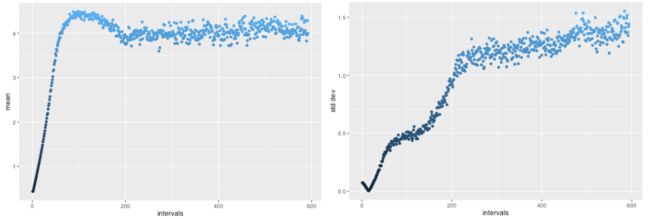
超过2万训练回合, 平均 G 的输出过度 4.0, 但然后回来在一个相当稳定, 正确的范围 (左)。同样, 标准偏差最初下落在错误方向, 但然后上升到期望1.25 范围 (正确), 匹配 R。
# ##### MODELS: Generator model and discriminator model

class Generator(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Generator, self).__init__()
        self.map1 = nn.Linear(input_size, hidden_size)
        self.map2 = nn.Linear(hidden_size, hidden_size)
        self.map3 = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        x = F.elu(self.map1(x))
        x = F.sigmoid(self.map2(x))
        return self.map3(x)

class Discriminator(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Discriminator, self).__init__()
        self.map1 = nn.Linear(input_size, hidden_size)
        self.map2 = nn.Linear(hidden_size, hidden_size)
        self.map3 = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        x = F.elu(self.map1(x))
        x = F.elu(self.map2(x))
        return F.sigmoid(self.map3(x))

def extract(v):
    return v.data.storage().tolist()

def stats(d):
    return [np.mean(d), np.std(d)]

def decorate_with_diffs(data, exponent):
    mean = torch.mean(data.data, 1, keepdim=True)
    mean_broadcast = torch.mul(torch.ones(data.size()), mean.tolist()[0][0])
    diffs = torch.pow(data - Variable(mean_broadcast), exponent)
    return torch.cat([data, diffs], 1)

d_sampler = get_distribution_sampler(data_mean, data_stddev)
gi_sampler = get_generator_input_sampler()
G = Generator(input_size=g_input_size, hidden_size=g_hidden_size, output_size=g_output_size)
D = Discriminator(input_size=d_input_func(d_input_size), hidden_size=d_hidden_size, output_size=d_output_size)
criterion = nn.BCELoss()  # Binary cross entropy: http://pytorch.org/docs/nn.html#bceloss
d_optimizer = optim.Adam(D.parameters(), lr=d_learning_rate, betas=optim_betas)
g_optimizer = optim.Adam(G.parameters(), lr=g_learning_rate, betas=optim_betas)

for epoch in range(num_epochs):
    for d_index in range(d_steps):
        # 1. Train D on real+fake
        D.zero_grad()

        #  1A: Train D on real
        d_real_data = Variable(d_sampler(d_input_size))
        d_real_decision = D(preprocess(d_real_data))
        d_real_error = criterion(d_real_decision, Variable(torch.ones(1)))  # ones = true
        d_real_error.backward() # compute/store gradients, but don't change params

        #  1B: Train D on fake
        d_gen_input = Variable(gi_sampler(minibatch_size, g_input_size))
        d_fake_data = G(d_gen_input).detach()  # detach to avoid training G on these labels
        d_fake_decision = D(preprocess(d_fake_data.t()))
        d_fake_error = criterion(d_fake_decision, Variable(torch.zeros(1)))  # zeros = fake
        d_fake_error.backward()
        d_optimizer.step()     # Only optimizes D's parameters; changes based on stored gradients from backward()

    for g_index in range(g_steps):
        # 2. Train G on D's response (but DO NOT train D on these labels)
        G.zero_grad()

        gen_input = Variable(gi_sampler(minibatch_size, g_input_size))
        g_fake_data = G(gen_input)
        dg_fake_decision = D(preprocess(g_fake_data.t()))
        g_error = criterion(dg_fake_decision, Variable(torch.ones(1)))  # we want to fool, so pretend it's all genuine

        g_error.backward()
        g_optimizer.step()  # Only optimizes G's parameters

    if epoch % print_interval == 0:
        print("%s: D: %s/%s G: %s (Real: %s, Fake: %s) " % (epoch,
                                                            extract(d_real_error)[0],
                                                            extract(d_fake_error)[0],
                                                            extract(g_error)[0],
                                                            stats(extract(d_real_data)),
                                                            stats(extract(d_fake_data))))

训练结果

经过2万训练回合, 平均 G 的输出过度 4.0, 但然后回来在一个相当稳定, 正确的范围 (左)。同样, 标准偏差最初下落在错误方向, 但然后上升到期望1.25 范围 (正确), 匹配 R。

图片.png

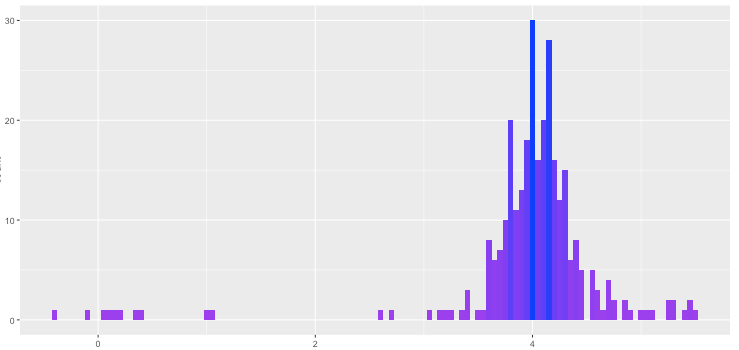
由 G自动生成的最终分配

参考链接
到底什么是生成式对抗网络
火热的生成对抗网络(GAN),你究竟好在哪里
Generative Adversarial Networks (GANs) in 50 lines of code (PyTorch)