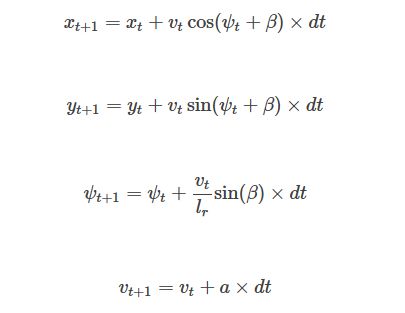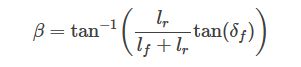- 将PID控制应用于无人车的问题
PID作为一种反馈控制方法,因其简单易实现被大量应用。但是在实际的车辆控制中,车辆往往不能立刻执行我们所下的指令,这其中存在一定的延迟,也就是说,我们的控制指令会在“未来的车辆状态”被执行,但是,由于PID是一种反馈控制,控制的指令使用当前车辆所处的状态决定的,然而当制动的指令被执行的时候,由于存在一定的延迟,车辆已经处于“未来的状态“了,在这个”未来的状态”使用这个指令去制动就会有一定的危险性。这是在无人车控制中使用PID算法的最大问题。
- 什么是模型预测控制
模型预测控制(MPC)是一种致力于将更长时间跨度、甚至于无穷时间的最优化控制问题,分解为若干个更短时间跨度,或者有限时间跨度的最优化控制问题,并且在一定程度上仍然追求最优解。模型预测控制由如下三个要素组成:
预测模型:预测模型能够在短时间内很好地预测系统状态的变化
在线滚动优化:通过某种最优化算法来优化未来一段短时间的控制输入,使得在这种控制输入下预测模型的输出与参考值的差距最小
反馈校正:到下一个时间点根据新的状态重新进行预测和优化
下面我们分别从这三个方面来讨论模型预测控制理论。
- 预测模型
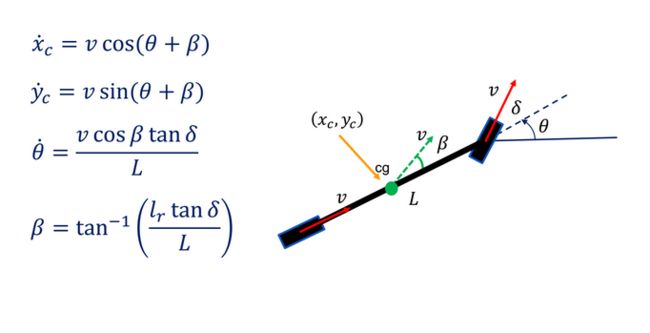
在本文中,我们使用运动学自行车模型作为预测模型,它的形式如下:
那么各个状态量的更新公式如下:
基于以上的公式,在给定一个控制指令的情况下,我们的这个预测模型能够根据运动学的规律计算出 dt时间以后车辆的状态 (x,y,ψ,v),这个预测模型(自行车模型)本身是建立在一定的假设前提的,所以计算出来的状态只是理论上车辆的可能状态。
我们从下图的情况出发进行讨论,下图是一条弯道,图中的实线是我们的参考线,我们控制的目标是让车辆尽量沿着参考线行驶: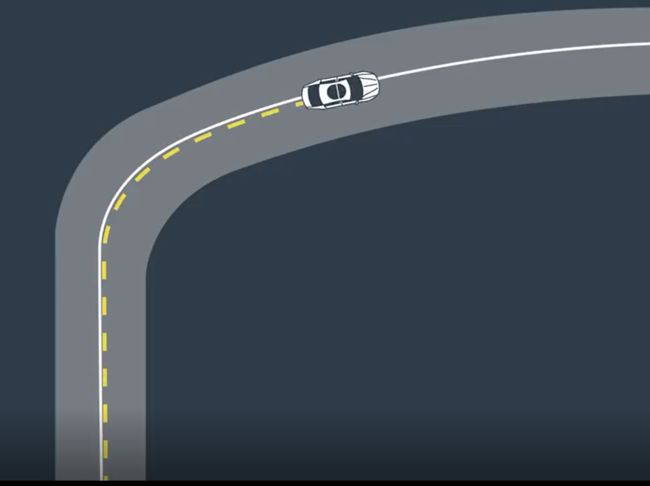
我们选取10个 dt,假设 dt=0.05s ,那么根据预测模型,在已知一组控制输入的前提下,我们可以计算出车辆在未来 0.5s的状态(本质上是一些离散的状态),如下图中的虚线所示:
- 在线滚动优化
那么现在问题就变成了一个最优化的问题,参照我们在神经网络优化中的经验,首先我们需要定义损失函数(Loss function),在本问题中,我们首先想到的一个损失函数就是我们的模型预测的轨迹和参考线之间的“差距”, 即 CTE(Cross Track Error),我们优化的目标就是找出一组控制量(即 (a,δf)油门刹车系数和方向盘转角),使得我们的Loss function最小化。
上文中我们只考量未来10个时间间隔内的模型预测,所以i的取值范围是 (1,10)![]() 是预测点到实际参考线的距离。为了完善我们的控制,我们可以给我们的损失函数添加更多的项,比如说我们不仅仅想控制车辆按照参考线行驶,还想控制车辆在这个短时间范围内在每个点上的速度,那么就可以在损失函数添加一项速度的平方差:
是预测点到实际参考线的距离。为了完善我们的控制,我们可以给我们的损失函数添加更多的项,比如说我们不仅仅想控制车辆按照参考线行驶,还想控制车辆在这个短时间范围内在每个点上的速度,那么就可以在损失函数添加一项速度的平方差: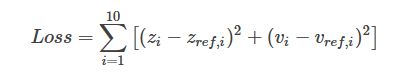
再进一步,损失函数还可添加许多项使控制变得更加平滑,比如我们希望油门系数不要突变(即缓慢的才油门和刹车,这样乘客的体验会更加舒适),那么我们就可以将前后两个油门系数的差值的平方作为一项加入到损失函数中: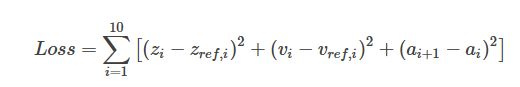
以此类推,损失函数还可以更加完善,损失函数设计得越合理,模型预测控制的输出也就也符合人的需求。当然,除了损失函数意外,我们的这个最优化问题中的变量还是 带约束的 ,比如说车辆的前轮转角 δf
的取值范围,车辆油门系数 a的取值范围(通常我们取值为-1到1,-1意味着满刹车,1意味着满油门)。 PID控制中遇到的制动延迟问题也可以通过添加约束来解决 ,具体来说:
假设我们车辆的制动延迟是 100ms, 本文中模型采用10步预测,每步间隔为 50ms ,即模型预测的前两步实际上是制动延迟的时间内,即实际上这两步中车辆仍然在执行上一个状态的制动指令,那么为了让模型更加贴近实际,我们就约束这2步的制动指令,即 (a,delta_f)为上一状态的指令,这样,我们的模型预测控制就将制动延迟考虑了进来。
- 反馈矫正
如图所示是MPC的简化示意图,可以看出,MPC本质上还是一种反馈控制,当我们通过最优化方法得到一组控制输出以后(本例中就是未来10步的控制输出),车辆执行控制指令,并且继续以一定的频率反馈当前车辆的状态 zt。这个状态会被同时输入到路径规划模块以及MPC控制模块,路径规划模块会依据新的车辆状态,结合感知模块的信息以及地图信息重新做出规划。MPC则根据新的参考路径和车辆当前状态进行新一轮的预测控制。需要注意的是,车辆真实状态的反馈并不是一个预测时间段的控制执行完以后才反馈的,反馈的时间间隔往往小于一个预测时间段(在本文的例子中,预测时间段长度为 0.05×10=0.5s)。
- 小结
通过使用不同的预测模型和损失函数,可以构造出各种模型预测控制器,但是,总的来说,模型预测控制往往可以分解成如下几步:
1. 从 t时刻开始,预测未来 a 步系统的输出信号
2. 基于模型的控制信号以及相应的输出信号,构造损失函数,并且通过调整控制信号最优化损失函数
3. 将控制信号输入到系统
4. 等到下一个时间点,在新的状态重复步骤