每天一篇系列:
强化知识体系,查漏补缺。
欢迎指正,共同学习!
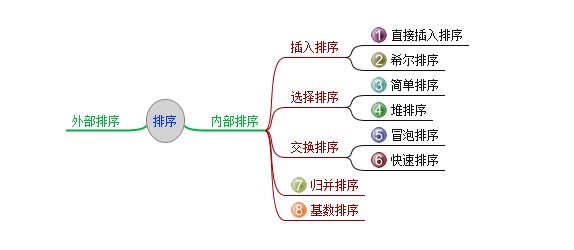
数据结构中的八种排序方法:
1.直接插入排序法
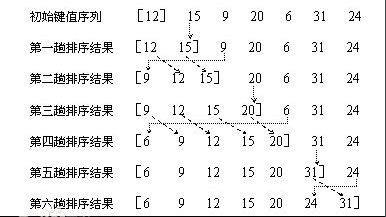
按个人理解就是从左至右把队列中的每一项与其前面已经排序好的项作比较,小则如同插入的方式交换位置,时间复杂度是O(N2)
/**
* 插入排序
*/
public static class InsertSort {
public static void test() {
int[] src = { 12, 15, 9, 20, 6, 31, 24 };
insertSort(src);
}
public static void insertSort(int[] sort) {
print(sort);
int j;
//外层循环的每一项可以看作对比因子
for (int i = 1; i < sort.length; i++) {
//把这个对比项提前保存起来,防止替换时被覆盖了
int item = sort[i];
//这里的循环可以理解为每次重新整理从左至右已经排列好的队列,可以理解为搬凳子
for (j = i; j > 0 && (item < sort[j - 1]); j--) {
sort[j] = sort[j - 1];// 相当于把位置挪出一个来
}
sort[j] = item;// 注意 这里是j--后的处理 所以是把值小的放到了挪出来的位置上
System.out.print(i + " round: ");
print(sort);
}
}
}
12 15 9 20 6 31 24
1 round: 12 15 9 20 6 31 24
2 round: 9 12 15 20 6 31 24
3 round: 9 12 15 20 6 31 24
4 round: 6 9 12 15 20 31 24
5 round: 6 9 12 15 20 31 24
6 round: 6 9 12 15 20 24 31
2.希尔排序法
希尔排序又叫缩小增量排序,是基于插入排序的一种算法,从队列中间开始把后半部分的项与前半部分的对应项(差值就是增量)作比较,小则交换位置,排序完后相对位置上就是左小右大,再从之前的位置的二分之一位置(差值也就减小了),实质上就是先按n的增量排序一次,让后然n/2再排序一次,直到增量为1最后再排序一次。时间复杂度是O(N2)
/**
* 希尔排序
*/
public static class ShellSort {
public static void test() {
int[] src = { 49,38,65,97,76,13,27,49,55,4 };
shellSort(src);
}
public static void shellSort(int[] sort) {
print(sort);
int round = 0;
for (int i = sort.length / 2; i > 0; i /= 2) {
for (int j = i; j < sort.length; j++) {
int item = sort[j];
int k;
boolean switched = false;
for (k = j; k >= i; k -= i) {
if (item < sort[k - i]) {
switched = true;
sort[k] = sort[k - i];
} else {
break;
}
}
sort[k] = item;
if (switched) {
print(sort);
}
}
System.out.print(round++ + " round: ");
print(sort);
}
}
}
49 38 65 97 76 13 27 49 55 4
13 38 65 97 76 49 27 49 55 4
13 27 65 97 76 49 38 49 55 4
13 27 49 97 76 49 38 65 55 4
13 27 49 55 76 49 38 65 97 4
13 27 49 55 4 49 38 65 97 76
0 round: 13 27 49 55 4 49 38 65 97 76
4 27 13 55 49 49 38 65 97 76
4 27 13 49 49 55 38 65 97 76
4 27 13 49 38 55 49 65 97 76
1 round: 4 27 13 49 38 55 49 65 97 76
4 13 27 49 38 55 49 65 97 76
4 13 27 38 49 55 49 65 97 76
4 13 27 38 49 49 55 65 97 76
4 13 27 38 49 49 55 65 76 97
2 round: 4 13 27 38 49 49 55 65 76 97
3.简单排序法(或者叫做选择排序)
按个人理解就是从待排序序列中,找到最小的元素,与对比元素交换位置。
/**
* 简单排序
*/
public static class SimpleSort {
public static void test() {
int[] src = { 12, 15, 9, 20, 6, 31, 24 };
simpleSort(src);
}
public static void simpleSort(int[] sort) {
print(sort);
int j;
for (int i = 0; i < sort.length - 1; i++) {
int min = i;
//找到最小一项的位置
for (j = i; j < sort.length; j++) {
if (sort[j] <= sort[min]) {
min = j;
}
}
// 找到了更小的值 交换位置
if (min != i) {
int tmp = sort[i];
sort[i] = sort[min];
sort[min] = tmp;
}
System.out.print(i + " round: ");
print(sort);
}
}
}
12 15 9 20 6 31 24
0 round: 6 15 9 20 12 31 24
1 round: 6 9 15 20 12 31 24
2 round: 6 9 12 20 15 31 24
3 round: 6 9 12 15 20 31 24
4 round: 6 9 12 15 20 31 24
5 round: 6 9 12 15 20 24 31
4.堆排序法
堆排序是指利用堆积树的数据结构特点所设计的一种排序算法。用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
注:如果父节点的下标是i,那么左子节点的下标就是2i+1,右节点的下标就是2i+2.
个人的理解是首先将需要排序的序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。然后将其(最大值)与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,也就是按堆序列的方式来处理一个n-1的序列,反复执行后,就能得到一个有序序列。
public static class HeapSort {
public static void test() {
int[] src = new int[] { 1, 0, 10, 20, 3, 5, 6, 4, 9, 8, 12, 17, 34, 11 };
buildMaxHeapify(src);
heapSort(src);
}
/**
* 左子节点position注意括号,加法优先级更高
*
* @paramcurrent
* @return
*/
private static int getChildLeftIndex(int current) {
return (current*2) + 1;
}
/**
* 右子节点position
*
* @paramcurrent
* @return
*/
private static int getChildRightIndex(int current) {
return (current*2) + 2;
}
/**
* 排序,最大值放在末尾,data虽然是最大堆,在排序后就成了递增的
*
* @paramdata
*/
private static void heapSort(int[] data) {
//末尾与头交换,交换后末尾就是最大值,然后对剩下未处理的序列再进行堆排序处理
for (int i = data.length - 1; i > 0; i--) {
int temp = data[0];
data[0] = data[i];
data[i] = temp;
maxHeapify(data, i, 0);
print(data);
}
}
/**
* 创建最大堆
*
* @paramdata
* @paramheapSize需要创建最大堆的大小,一般在sort的时候用到,因为最多值放在末尾,末尾就不再归入最大堆了
* @paramindex当前需要创建最大堆的位置
*/
private static void maxHeapify(int[] data, int heapSize, int index) {
// 当前点与左右子节点比较
int left = getChildLeftIndex(index);
int right = getChildRightIndex(index);
int largest = index;
// 如果左子节点比父节点大,则需要和父节点交换
if (left < heapSize && data[index] < data[left]) {
largest = left;
}
// 如果右子节点比父节点大,则需要和父节点交换
if (right < heapSize && data[largest] < data[right]) {
largest = right;
}
// 得到最大值后可能需要交换,如果交换了,其子节点可能就不是最大堆了,需要重新调整
if (largest != index) {
int temp = data[index];
data[index] = data[largest];
data[largest] = temp;
// 继续调整最大位置,直到找到节点最大值
maxHeapify(data, heapSize, largest);
}
}
private static void buildMaxHeapify(int[] data) {
// 从第一个非叶子结点从下至上,从右至左调整结构
int startIndex = data.length/2 - 1;
// 从尾端开始创建最大堆,每次都是正确的堆
for (int i = startIndex; i >= 0; i--) {
maxHeapify(data, data.length, i);
}
}
}
调整后的输出如下:
20 12 17 9 8 10 11 4 0 6 3 1 5 34
17 12 11 9 8 10 5 4 0 6 3 1 20 34
12 9 11 4 8 10 5 1 0 6 3 17 20 34
11 9 10 4 8 3 5 1 0 6 12 17 20 34
10 9 6 4 8 3 5 1 0 11 12 17 20 34
9 8 6 4 0 3 5 1 10 11 12 17 20 34
8 4 6 1 0 3 5 9 10 11 12 17 20 34
6 4 5 1 0 3 8 9 10 11 12 17 20 34
5 4 3 1 0 6 8 9 10 11 12 17 20 34
4 1 3 0 5 6 8 9 10 11 12 17 20 34
3 1 0 4 5 6 8 9 10 11 12 17 20 34
1 0 3 4 5 6 8 9 10 11 12 17 20 34
0 1 3 4 5 6 8 9 10 11 12 17 20 34
5.冒泡排序法
学习算法时的入门算法,原理很简单,大的往下"沉",小的往上"浮",每次对比后,保证左边的元素小于右边的元素,所以称之为冒泡。
/**
* 冒泡排序
*/
public static class BubbleSort {
public static void test() {
int[] src = { 12, 15, 9, 20, 6, 31, 24 };
bubbleSort(src);
}
public static void bubbleSort(int[] sort) {
print(sort);
int j;
//只需要sort.length - 1次对比
for (int i = 0; i < sort.length - 1; i++) {
//每次对比后右边序列已经是最大值就不需要继续比较了
//这里也是冒泡算法的优化之一,这里甚至还可以判断是否已经是排序好了,否则这里每次都是最坏情况全遍历
for (j = 0; j < sort.length - i - 1; j++) {
if (sort[j+1] < sort[j]) {
int tmp = sort[j];
sort[j] = sort[j + 1];
sort[j + 1] = tmp;
}
}
System.out.print(i + " round: ");
print(sort);
}
}
}
12 15 9 20 6 31 24
0 round: 12 9 15 6 20 24 31
1 round: 9 12 6 15 20 24 31
2 round: 9 6 12 15 20 24 31
3 round: 6 9 12 15 20 24 31
4 round: 6 9 12 15 20 24 31
5 round: 6 9 12 15 20 24 31
从输出可以看到是可以继续优化的,为了提高效率,已经是排序好后的序列后,最后多出来的几次轮询是可以省掉的。
6.快速排序法
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序。
三数取中法:选取开始,中间,结束位置的三个数作为比较值,然后进行排序。原则就是从左到右寻找比比较值大的,从右到左寻找比比较值小的,经过排序后左小右大的序列。
public static class QuickSort extends Sort {
public static String getTAG() {
return QuickSort.class.getSimpleName();
}
public static void test() {
int[] data = new int[MAX_DATA_SIZE];
copyData(src, data);
long cur = System.currentTimeMillis();
quickSort(data, 0, data.length - 1);
long cost = System.currentTimeMillis() - cur;
log.info(getTAG() + " costtime:" + cost + "\n");
testResult(getTAG(), data);
}
public static void quickSort(int[] src, int left, int right) {
if(left >= right){
return;
}
int index_item = (left + right) / 2;
int item = src[index_item];
if (src[right] < src[left]) {
swapData(src,left,right);
}
if (item < src[left]) {
swapData(src,left,index_item);
}
if (item > src[right]) {
swapData(src,index_item,right);
}
//排在倒数第二个
swapData(src,index_item,right-1);
int bucket = src[right-1];
int p_left = left + 1;
int p_right = right - 1 - 1;
while(true){
while(p_left < right && src[p_left] < bucket){
p_left++;
}
while(p_right > left && src[p_right] > bucket){
p_right--;
}
if(p_left < p_right){
swapData(src, p_left, p_right);
}else {
break;
}
}
if(p_left < right){
swapData(src,p_left,right-1);
}
quickSort(src, left, p_left-1);
quickSort(src, p_left+1, right);
}
public static void swapData(int[] src,int index1,int index2){
int tmp = src[index1];
src[index1] = src[index2];
src[index2] = tmp;
}
}
7.归并排序
个人理解就是先把序列从中间开始各自排序为一个有序序列,然后再操作两个有序序列,逐次对比两个序列元素大小,放置到新的序列中。这种排序利用完全二叉树特性,平均时间复杂度均为O(nlogn)。
/**
* 归并排序
*/
public static class MergeSort extends Sort {
public static String getTAG() {
return MergeSort.class.getSimpleName();
}
public static void test() {
int[] data = new int[MAX_DATA_SIZE];
copyData(src, data);
int[] tmp = new int[data.length];
long cur = System.currentTimeMillis();
sort(data, 0, data.length - 1, tmp);
long cost = System.currentTimeMillis() - cur;
log.info(getTAG() + " costtime:" + cost + "\n");
testResult(getTAG(), data);
}
public static void sort(int[] src, int left, int right, int[] dst) {
if (left < right) {
int mid_index = (left + right) / 2;
sort(src, left, mid_index, dst);
sort(src, mid_index + 1, right, dst);
mergeSort(src, left, mid_index, right, dst);
}
}
public static void mergeSort(int[] src, int left, int mid, int right,
int[] dst) {
int i = left;
int j = mid + 1;
int t = 0;
for (; i <= mid && j <= right;) {
//把左边区域放置小元素,右边区域放置大元素
if (src[i] <= src[j]) {
dst[t++] = src[i++];
} else {
dst[t++] = src[j++];
}
}
while (i <= mid) {
dst[t++] = src[i++];
}
while (j <= right) {
dst[t++] = src[j++];
}
t = 0;
while (left <= right) {
src[left++] = dst[t++];
}
}
}
orignal data:[ 111 43 108 86 5 31 4 7 36 82 88 114 ]
MergeSort costtime:0
MergeSort sort result:4 5 7 31 36 43 82 86 88 108 111 114
8.基数排序
可以理解为分别按个、十、百、千、万来做关键词分别入桶。即首先根据每个数据个位数的数值,在遍历数据时将它们各自分配到编号0至9的桶,入桶的数据序列然后按数据十位数的数值重新入桶,依此类推直到把最高位分配完就完成了排序。
private static void radixSort(int[] array) {
// 找到数组中的最大值
int max = array[0];
for (int i = 0; i < array.length; i++) { // 找到数组中的最大值
if (array[i] > max) {
max = array[i];
}
}
int keysNum = 0; // 关键字的个数,我们使用个位、十位、百位...当做关键字,所以关键字的个数就是最大值的位数
while (max > 0) {
max /= 10;
keysNum++;
}
List> buckets = new ArrayList>();
for (int i = 0; i < 10; i++) { // 每位可能的数字为0~9,所以设置10个桶
buckets.add(new ArrayList()); // 桶由ArrayList构成
}
for (int i = 0; i < keysNum; i++) { // 由最次关键字开始,依次按照关键字进行分配
for (int j = 0; j < array.length; j++) { // 扫描所有数组元素,将元素分配到对应的桶中
// 取出该元素对应第i+1位上的数字,比如258,现在要取出十位上的数字,258%100=58,58/10=5
int key = array[j] % (int) Math.pow(10, i + 1)
/ (int) Math.pow(10, i);
buckets.get(key).add(array[j]); // 将该元素放入关键字为key的桶中
}
// 分配完之后,将桶中的元素依次复制回数组
int counter = 0; // 元素计数器
for (int j = 0; j < 10; j++) {
ArrayList bucket = buckets.get(j); // 关键字为j的桶
while (bucket.size() > 0) {
array[counter++] = bucket.remove(0); // 将桶中的第一个元素复制到数组,并移除
}
}
}
}
把以上8种排序思想介绍了一遍,下面来看看各种排序执行效率的情况分析:
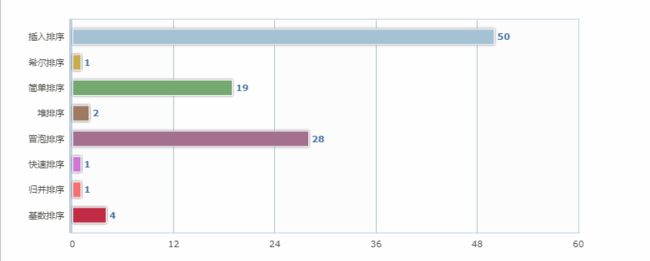
1K数据排序效率对比:
InsertSort costtime:50
ShellSort costtime:1
SimpleSort costtime:19
HeapSort costtime:2
BubbleSort costtime:28
QuickSort:1
MergeSort costtime:1
RadixSort costtime:4
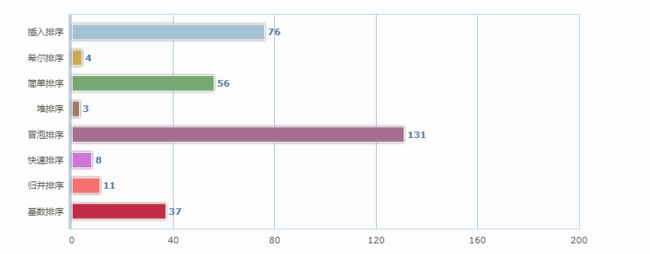
1W数据排序效率对比:
InsertSort costtime:76
ShellSort costtime:4
SimpleSort costtime:56
HeapSort costtime:3
BubbleSort costtime:131
QuickSort:8
MergeSort costtime:11
RadixSort costtime:37
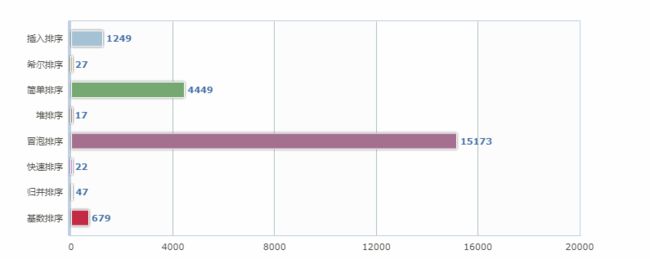
10W数据排序效率对比:
InsertSort costtime:1249
ShellSort costtime:27
SimpleSort costtime:4449
HeapSort costtime:17
BubbleSort costtime:15173
QuickSort:22
MergeSort costtime:47
RadixSort costtime:679
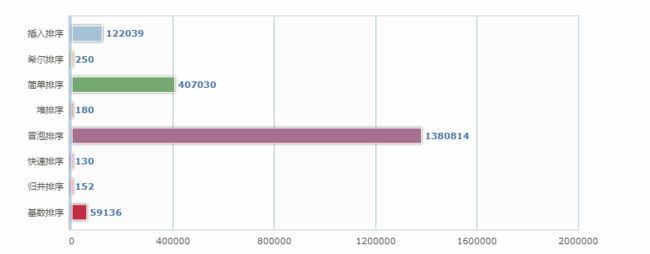
100W数据排序效率对比:
InsertSort costtime:122039
ShellSort costtime:250
SimpleSort costtime:407030
HeapSort costtime:180
BubbleSort costtime:1380814
MergeSort costtime:130
QuickSort costtime::152
RadixSort costtime:59136
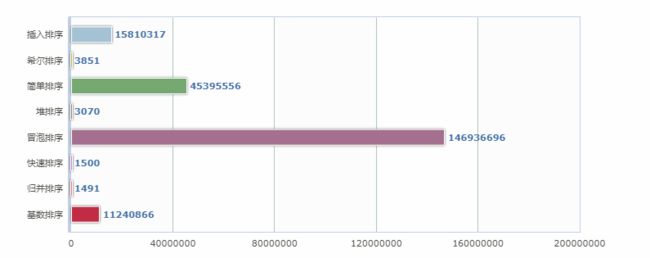
1000W数据排序效率对比:
InsertSort costtime:15810317
ShellSort costtime:3851
SimpleSort costtime:45395556
HeapSort costtime:3070
BubbleSort costtime:146936696
MergeSort costtime:1500
QuickSort costtime::1491
RadixSort costtime:11240866
可以看到堆排序、归并排序、基数排序在数据批量小的时候并没有很明显的体现出效率优势,而在数据批量大时体现出的效率非常高。
时间复杂度:
在直接插入排序,简单排序,冒泡排序中,问题规模为n,又需要比较n次,所以平均时间复杂度为O(n²)。
在希尔排序、堆排序、快速排序、归并排序的排序中,问题规模通过分治法消减为logN次,所以平均时间复杂度为O(nlogn)。
基数排序的时间复杂度为O(N*M),其中N为数据个数,M为数据位数。
稳定性定义:
在排序序列中有2个或以上的相同数值在排序前后,排序序列中的前后位置如果发生变化就是不稳定,如果前后位置没有发生变化则是稳定的。而稳定的算法包括直接插入排序法、冒泡排序法、归并排序法和基数排序法。