概念
递归特点:调用自身,有结束条件。
注意区分下面两种递归:
def func(x):
if x > 0:
print(x)
func(x - 1)
func(5)输出 5 4 3 2 1
def func2(x):
if x > 0:
func2(x - 1)
print(x)
func(5)输出 1 2 3 4 5
时间复杂度
是一个单位,也是一个估计值,这也就表示下面的代码:
print(x)
print(x)
print(x)
不是O(3) 而是 O(1)
for i in range(n):
print(x)
for j in range(n):
print(x)
不是O(N^2 + N) 而是 O(N^2)
for i in range(n):
for j in range(i):
print(x)
不是O(N^2 / 2)而是 O(N^2)
而这段代码:
while i > 0:
print(i)
i = i // 2
他的时间复杂度为O(logN),假设输入64 则输出 64 32 16 8 4 2 ,即 6 次,则2的6次方为64,即log2 64 = 6(以2为底64的对数)
如何一眼粗略的看出复杂度?
- 是否有循环减半操作,减半就logN
- 几层循环就N的几次方
空间复杂度,用来评估算法内存占用大小的一个式子。
用几个变量的时候就是O(1),用一个列表的时候就是O(N)。
列表查找分为,
- 顺序查找
- 二分查找
tips:不要在一个递归函数上加装饰器,如果想加装饰器,则需要新开一个函数,加上装饰器,然后返回递归函数
tips:尾递归(return 递归函数)的运行速度跟正常函数一样。
tips:切片为什么慢?因为它要重新再创建一个列表或字符串来保存切好的。
二分查找
二分查的前提条件:有序列表,然后设立两个指针 low 和 high,得到他们的中间值 mid ,通过对待查找的值与候选区中间值的比较,可以使候选区减少一半。
def binary_search(li, target):
low = 0
high = len(li) - 1
while low <= high:
mid = (low + high) // 2
if li[mid] == target:
return mid
elif li[mid] > target:
high = mid - 1
elif li[mid] < target:
low = mid + 1
return
排序:
首先看 LowB 三人组,冒泡,选择,插入。
冒泡排序
按升序排时,列表每两个相邻的数,如果前边的比后边的大,则交换着两个数。
一些名词:
一趟:表示的是当交换到最后,把最大的数交换上去的过程。趟数从0开始。
有序区,已经有序的区域,
无序区,还无序的区域。
冒泡的趟数为 N - 1,N 是数组长度,要减一的原因是当冒泡排到最后一个时,数组的最后一个也自然的有序了(肯定是最小的),而趟数就是最外层的循环。
趟数里的操作次数,假设趟数为 i ,则趟数操作次数为 N - i - 1,因为每完成一趟,则需要操作的数就减少一个,而交换时,不用交换有序区(因为交换是两个数的操作),所以减一。而趟数里的操作就是内层循环。
def bubble_sort(li):
# 这里长度不用减一的原因是,range操作取不到最后,就相当于帮我们减一了。
n = len(li)
for i in range(n - 1):
for j in range(n - i - 1):
if li[j] > li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
因为有两层循环,所以时间复杂度为O(N^2)
优化:如果冒泡排序中执行一趟而没有发生交换,则表明列表已经是有序的了,可以直接结束算法。可以通过设置一个 flag,通过 flag 来判断是否发生了交换。
def bubble_sort(li):
for i in range(len(li) - 1):
flag = False
for j in range(len(li) - i - 1):
if li[j] > li[j + 1]:
li[j], li[j + 1] = li[j + 1], li[j]
flag = True
if not flag:
break
但是时间复杂度还是O(N^2),因为还是两层循环,不过当遇到最好情况(已经排序好),时间复杂度是O(1)
选择排序
一趟遍历选出最小的数,放第一个位置,再一趟遍历选出剩余列表最小的,周而复始。
def select_sort(li):
n = len(li)
for i in range(n - 1):
# 最开始假定下标为i 的元素是最小的
min_loc = i
# 因为设定 i 为最小的,所以range时从 i + 1 开始,就不用重复判断i 是否是最小的
for j in range(i + 1, n - 1):
if li[j] < li[min_loc]:
min_loc = j
# 当一趟执行完后,找到最小的元素的下标,然后和下标为 i 的进行交换
li[i], li[min_loc] = li[min_loc], li[i]
复杂度 O(N^2)
插入排序
列表被分为有序区和无序区,最初有序区只有一个元素,每次从无序区选择一个元素,插入到有序区的位置,直到无序区变空。(可以想象打牌时抓牌的场景)。
def insert_sort(li):
n = len(li)
# 最初有序区有一个元素,所以从 1 开始, i 代表第几次来排序,也表示排的第几个元素,因为每次就排好一个元素
for i in range(1, n):
tmp = li[i]
# 这个需要排序的来和他前面位置的比较大小
j = i - 1
while j >= 0 and li[j] > tmp:
# 右移过程
li[j + 1] = li[j]
j -= 1
# 因为右移过程会伴随的 j - 1 的操作,所以这里想将tmp存到合适位置j要 j + 1
li[j + 1] = tmp
复杂度O(N^2)
快速排序
取一个元素p(一般是第一个),使元素p归位(到他应该的位置),并使列表分为两部分,左边都比p小,右边都比p大。然后递归完成排序。
def quick_sort(li, left, right):
# 递归终止条件,不等于的原因是有两个元素才需要进行排序
if left < right:
# 使元素归位,mid 是放置好的元素的下标
mid = partition(li, left, right)
quick_sort(li, left, mid - 1)
quick_sort(li, mid + 1, right)
def partition(li, left, right):
刚开始将最左边的数存起来,这样最左边就出现空位了,然后准备动右边的指针
tmp = li[left]
while left < right:
# 当右边的数比这个存起来的左边数大,继续动右边指针,因为我们最终目的是想要右边的数大,左边数小
while left < right and li[right] >= tmp:
right -= 1
# 当出现右边数比左边数小的情况,则交换这两个数,然后交换后,右边出现空位,开始动左边指针
li[left] = li[right]
while left < right and li[left] <= tmp:
left += 1
li[right] = li[left]
# 运行到这里,left 已经等于 right 了,而且还剩一个空位,就是tmp的应该到的位置
li[left] = tmp
return left
复杂度,NlogN,复杂度原因,不严谨的假设有64个元素,
64
第一遍分为了 32 32
32
第二遍分为了 16 16
16
第三遍分为了 8 8
8
第四遍分为了 4 4
4
第五遍分为了 2 2
2
第六遍分为了 1 1
所以就有6次partition(logN),然后一次partition其实数组被遍历了一遍,所以为NlogN
tips:Python系统内置的sort,非常快,但是其实时间复杂度跟快排是一个数量级(NlogN),那他快在哪?
因为它是用C写的,所以比我们手写的快排快。所以还是老老实实的用系统自带的sort吧。
快排的问题:
- 最差情况
| 类型 | 最好情况 | 一般情况 | 最差情况 |
|---|---|---|---|
| 快排 | O(NlogN) | O(NlogN) | O(N^2)[倒序的时候,每次partition都只减少了一次而不是分成两半] |
| 冒泡 | O(N) | O(N^2) | O(N^2) |
- 递归最大深度限制
当递归次数超过一定范围,程序就挂了,所以需要设置递归最大深度
import sys
sys.setrecursionlimit(N) # N 为设置的最大深度
堆排序
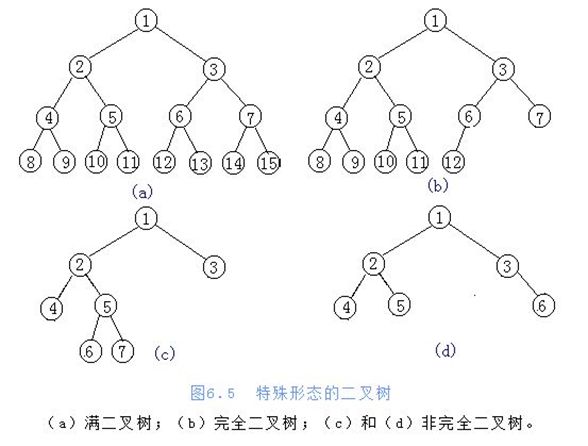
进化流程:树 -> 二叉树(度不超过2的树) -> 完全二叉树 -> 大根堆 / 小根堆
概念
- 根节点,叶子节点
- 树的深度(高度)[层数]
- 树的度[最大的节点的分叉数]
- 孩子节点 / 父节点
-
子树
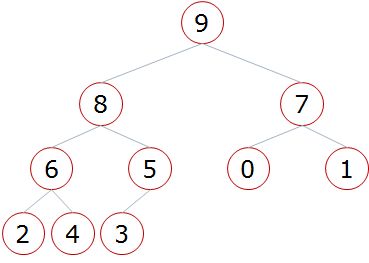
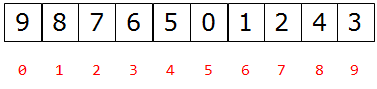
二叉树存储方式:
- 链式存储方式
- 顺序存储方式(列表)[我们下面用的]
父节点和左孩子节点的编号下标有什么关系?
i ~ 2i + 1 当父节点为i 时,左孩子节点为2i + 1
父节点和右孩子节点的编号下标有什么关系?
i ~ 2i + 2
所以,可以通过以上规律从父亲找到孩子或者从孩子找到父亲
堆,一颗特殊的完全二叉树,分为大根堆和小根堆
大根堆:满足任一节点都比其孩子节点大
小根堆:满足任一节点都比其孩子节点小
当根节点的左右子树都是堆,但自身不是堆的时候,可以通过一次向下的调整来将其变换成一个堆。
堆排序过程:
- 建立堆
- 得到堆顶元素,为最大元素(这里用的大根堆)
- 去掉堆顶,将堆的最后一个元素放到堆顶,此时可通过一次调整重新使堆有序
- 堆顶元素为第二大元素
- 重复步骤3,直到堆变空
一次调整的.
# low ~ high 范围的小堆,low 是堆顶
def shif(li, low, high):
# i 永远指向的是根节点
i = low
j = 2 * i + 1
tmp = li[i]
while j <= high:
# 如果有右孩子(j tmp:
li[i] = li[j]
i = j
j = 2 * i + 1
# 当当前范围的根节点是最大时,跳出循环
else:
break
# 最后将存储的tmp 放到调整完后的节点位置。
li[i] = tmp
堆排序.
def heap_sort(li):
n = len(li)
# 最后一个有孩子的父亲的下标,数学证明出来的,记住即可
last_father_index = n // 2 - 1
# 循环顺序是从最后一个有孩子的父亲 -> 堆顶,倒着循环的。第二个参数为 -1 是因为range顾头不顾尾,想要取到堆顶,也就是index为0的位置,就要把他设为 -1
# 注意这里不要被这个循环迷惑,这个循环作用就是找到根节点,以便下面的调整操作
for i in range(last_father_index, -1, -1):
# 这里可以永远写 n - 1(堆的最后一个)
sift(li, i, n - 1)
############# 这样一个堆就建立好了 #############
for i in range(n - 1, -1, -1):
li[0], li[i] = li[i], li[0]
sift(li, 0, i - 1)
############# 以上操作就是去掉堆顶,将堆的最后一个元素放到堆顶,
# 只是这里为了节省新开列表的空间,将要出来的堆顶存到了原来最后一个元素的位置,然后在调整时,通过改变high的范围来减小堆的范围,而且,由于他将最大的存在最后面,所以最后排出的列表是升序的。########
li_new = []
for i in range(n - 1, -1, -1):
li_new.append(li[0])
li[0] = li[i]
sift(li, 0, n - 1)
return li_new
############ 这是第二种写法,比较好理解,就是新开一个列表,来存通过依次出数处理的堆顶元素,
# 但是要注意的是他对原列表不会排序,而是返回一个已经排序好的新列表。 ##########
复杂度为O(NlogN)
归并排序
归并:将两段有序的列表合成为一个有序列表的过程。
一次归并.
# low: 第一段有序列表的开头
# mid: 第一段有序列表的结尾,所以mid + 1 就为第二段有序列表的开头
# high: 第二段有序列表的结尾
def merge(li, low, mid, high):
i = low
j = mid + 1
ltmp = []
# 两边都必须有数,这样才能比较两边数的大小
while i <= mid and j <= high:
if li[i] < li[j]:
ltmp.append(li[i])
i += 1
else:
ltmp.append(li[j])
j += 1
# 比到最后,肯定有一段列表有剩余,则将剩余全部添加进新列表
while i <= mid:
ltmp.append(li[i])
i += 1
while j <= mid:
ltmp.append(li[j])
j += 1
# 这里用切片不会减慢速度。因为它在等号左边。
li[low:high + 1] = ltmp
归并排序.
# 因为这里是先调用merge_sort递归,再进行merge操作,
# 所以就会将列表越分越小,直至分成一个元素,而一个元素时就是有序的。
# 这样merge操作的条件就满足了。然后通过merge将他们合并。
# 总结下来就是先分解,后合并。
def merge_sort(li, low, high):
if low < high:
mid = (low + high) // 2
merge_sort(li, low, mid)
merge_sort(li, mid + 1, high)
merge(li, low, mid, high)
时间复杂度:O(nlogn)
空间复杂度:O(n)
快速排序、堆排序、归并排序-小结
三种排序算法的时间复杂度都是O(nlogn)
一般情况下,就运行时间而言:
快速排序 < 归并排序 < 堆排序
三种排序算法的缺点:
- 快速排序:极端情况下排序效率低
- 归并排序:需要额外的内存开销
- 堆排序:在快的排序算法中相对较慢
希尔排序
希尔排序是一种分组插入排序算法
希尔排序每趟并不使得某些元素有序,而是使整体数据越来越接近有序,最后一趟使得所有数据有序。
def shell_sort(li):
# gap表示分组的间隔
gap = len(li) // 2
while gap >= 1:
for i in range(gap, len(li)):
tmp = li[i]
# j表示每组的前一张牌,因为每组都是间隔为gap
j = i - gap
while j >= 0 and tmp < li[j]:
li[j+gap] = li[j]
j -= gap
li[i-gap] = tmp
gap /= 2
时间复杂度: O((1+τ)n) τ:tuo , 0 < τ < 1
一般认为是O(1.3n),比O(NlogN)慢