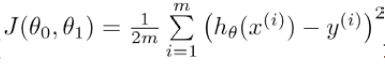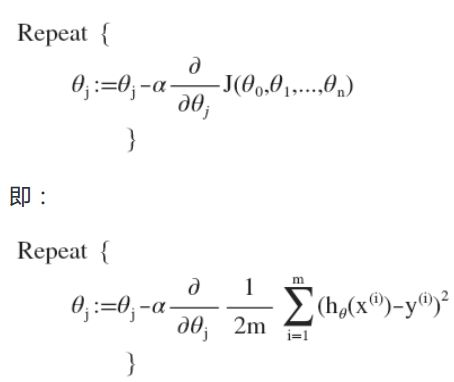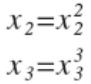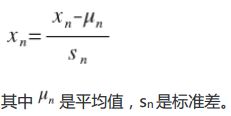自从选了《机器学习》这门课之后,感觉被杜老师拉入了神坑。课上接受着英语翻译的洗礼,课下还自虐的找可了份英语听力的挑战。我对机器学习还是比较有感的,虽然是坑,但是还是想努力填满这个坑。
课上老师指定的教材是英文版的《机器学习》,课下我跟着吴恩达老师学习网上课程《机器学习》,感兴趣的可以跟我一起去cousera上看吴恩达老师的视频(免费的哦)~我做个知识点的解释和总结~有兴趣的可以看看哟~
什么是机器学习
1.简介:
机器学习是一门多领域交叉学科,涉及到的学科有概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。机器学习并没有一致认同的定义,一个较为古老的定义如下:“机器学习研究的是如何赋予计算机在没有明确编程的情况下仍然能够学习的能力”;机器学习一个比较现代并且形式化的定义由Tom Mitchell在1998年给出的:“对于某个任务T和性能的衡量P,当计算机程序在任务T上的性能,经过P的衡量随着经验E的增长而增长,我们便称计算机程序能通过经验E学习该任务(翻译的太烂了,看英文吧:computer program is said to learn from experience E with respect to some task T and some performance measure P,if its performance on T,as measured by P,improves with experience E.在跳棋游戏的例子中,任务T就是玩跳棋游戏,P就是游戏的输赢,E则是一局又一局的游戏)”
2.应用
关于机器学习的应用例子也有很多:
a.数据库挖掘、
b.一些无法通过手动编程来编写的应用(如自然语言处理、计算机视觉)
c.一些自助式的程序(如推荐系统)
d.理解人类是如何学习的
3.机器学习的分类
机器学习分成两类:监督学习、非监督学习。(也有分成三类的:监督、半监督和非监督)下面的定义可以稍微看一下,后续的讲解中会说明什么是监督学习,什么是非监督学习。
(1)监督学习:对具有概念标记(分类)的训练样本进行学习,以尽可能对训练样本集外的数据进行标记(分类)预测。这里,所有的标记(分类)是已知的。
(2)无监督学习:对没有概念标记(分类)的训练样本进行学习,以发现训练样本几种的结构性知识。这里,所有的标记(分类)是未知的。
总而言之,机器学习就是机器学习人类思维的一个过程。人类的意识是一种非常奇妙的东西,假设1给你一顿图片让你去识别哪些图片中是王源,那些图片中是王俊凯,那些图片中既有王源又有王俊凯;假设2给你一顿图片让你去识别,没有任何别的提示,只是让你去识别。这两个假设都是机器学习中的分类问题,不同的是假设1的分类是已知的,所以是监督学习,假设2中的分类是未知的,所以是无监督学习。
接下来我们从浅入深去了解机器学习中的大小算法,没有顺序,大家一起学习吧~我学懂了哪个就和大家分享哪个~
线性回归算法
线性回归算法可以理解成,为N维空间中的一堆点找一条拟合的线的一个过程,而在找这条线的过程中用到了一种方法叫做——梯度下降算法,当然咱们潜意识应该认为可以用线性代数的方法,解方程就好了,当然当变量很少的时候我们解方程很简单,可是当变量太多的时候这会成为一件很麻烦的事情,因此有了梯度下降方法。梯度下降方法又依赖一个很重要的定义——损失函数。所以这一小节我们讲述:线性回归、损失函数、梯度下降三个部分。
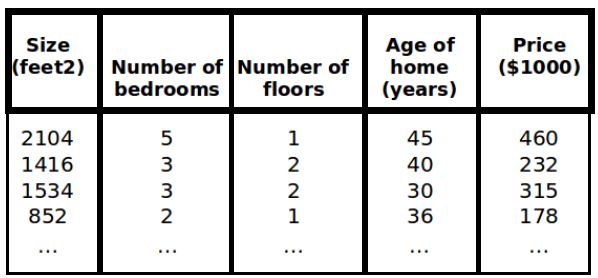
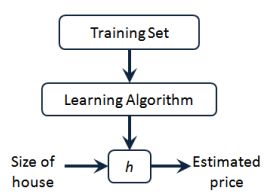
1.我们用吴恩达老师视频中房屋交易的例子去理解这个算法。假设某市房子的房价和对应房屋特征整理出训练集如下表1所示,房子的特征包括大小,卧室数目,楼层,年龄等。利用该例子构建一个模型,模型特征为(x1,x2,...,xn)。
对于这个回归问题,我们定义一些标记:
m代表训练集中实例的数目。
n表示特征的数量。
x代表特征/输入变量。
x(i)((i)是上角标)代表第i个训练实例,是特征矩阵中的第i行,是一个向量。
x(i)j((i)是上角标,j是下角标)代表特征矩阵第i行第j个特征,也就是第i个训练实例中 的第j个特征。
y代表目标变量/输出变量。
(x,y)代表训练集中的实例。
(x(i),y(i))((i)是上角标)代表第i个观察实例。
h代表学习算法的解决方案或者函数,也称为假设,可以表示为:hθ(x)=θ0+θ1x1+θ2x2+...+θnxn,公式(1)所示。此时,模型中的参数是一个n+1维的向量,任何一个训练视力也是n+1维的向量,特征矩阵X的维度是m*(n+1),因此可以简化成hθ(x)=θTX,如公式(2)所示。倘若只有一个特征,那么,hθ(x)=θ0+θ1x,如公式(3)所示。
2.损失函数
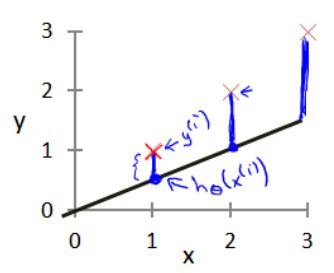
损失函数也称为代价函数,其实也可以理解为代价误差,对于线性回归的学习算法,参数θ的选择决定了我们得到的线相对于训练集的准确程度,模型预测值与训练集中实际值之间的差距(下图2中的蓝线所指)就是建模误差,因此得到代价函数,公式(4)所示。
代价函数越小,那么我们给出的学习算法将与训练集越契合,所以我们要做的是让代价函数最小。
3.梯度下降算法
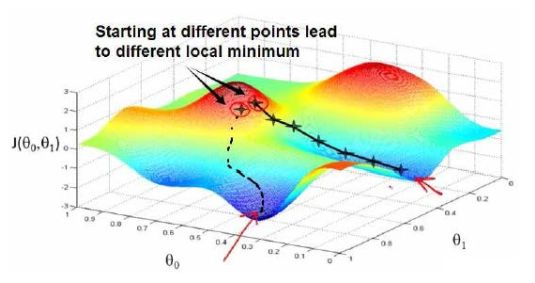
梯度下降是一个用来求函数最小值的算法,我们用来求出代价函数的最小值。梯度下降背后的思想是:开始时我们随机选择一个参数集合,计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数集合。我们持续这么做直到一个局部最小值,因为我们并没有尝试完所有的参数集合,所以不能确定是否得到了全局最小值,选择不同的初始参数集合,可能会找到不同的局部最小值。
接下来我们看一张图,这里是两个寻找损失函数最小值的过程。
批量梯度下降算法的公式为:
这个式子可以结合图去理解,对于一个关于θ的函数,怎么减小它呢,可以对它求导。求导之后可以知道当前关于θ的斜率,它决定了行走的方向往哪儿走是下降的。其中α是学习率,他决定了行走的步长。
对线性回归运用梯度下降法之后,关键在于求出代价函数的导数,算法可以改写成:
我们在最开始,选择一些列的参数值,计算所有的预测结果后,再给参数一个新值,如此循环直到收敛。
关于多项式回归,有时候线性回归并不能满足所有数据,因此有时候会用到多项式回归,我们可能会用到二次项模型或者三次项模型,如公式(6)和公式(7)所示,不用担心,我们可以令x2=x的平方,x3=x的三次方,即图4所示,从而将模型转换成线性回归模型。当然我们也可以直接采用多项式回归模型。
特征缩放
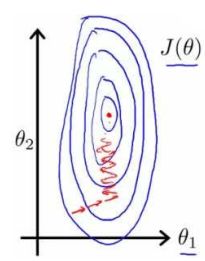
特征缩放可以简化梯度下降求线性回归函数最优解的过程。以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的直为 0-2000 平方英尺,而房间数量的直则是 0-5,以两个参数分别为横纵坐标,绘制代价函数的等高线图能看出图像会显得很扁,如图5所示,梯度下降算法需要非常多次的迭代才能收敛。我们应保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。
最简单的方法如下图6所示:
学习率
梯度下降算法迭代所少次才能收敛,可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。也可以用一些自动测试是否收敛的方法,例如将代价函数的变化直与某个阀值(例如 0.001)进行比较,但通常图表表达效果更好一些。梯度下降算法的每次迭代受到学习率的影响,如果学习率α过小,则达到收敛所需的迭代次数会非常高;如果学习率α过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
通常可以考虑尝试这些学习率:α=0.01,0.3,0.1,0.3,1,3,10
这周就到这里了,下周可能会更新逻辑回归算法~p.s.上面一直在讲梯度下降算法,其实作为高材生的你们肯定想到~求导为零解出来参数值就可以啦,可以的哦~先尝试正规方程的方法,求导为零去求解,如参数太多了再来尝试梯度下降算法吧。