按挑战程序设计竞赛介绍的顺序记录一遍学习DP的过程。
1. 01背包问题
问题如下:
有N个物品,每个物品(N[i])都有一定的体积(W[i]),和一定的价值(V[i])
现在给定一个背包,背包的容量为VBag
如何选择装进背包的物品,使背包中的物品价值总和最大?
动态规划的思想就是将一个大问题分解为易于解决的小问题,找到大问题对于小问题的递推关系,从而解决大问题。
对于01背包而言,多个物品如何选择很明显是一个不可解的问题
把题目中给的条件做一下变换,假设只有1个物品,就很好解了,如果背包能装下,就装。
再假设有两个物品,这时就要考虑一下背包的容量问题了。
1. 背包两个物品都能装下,最大价值就是两者之和
2. 如果只能装下其中之一,总的最大价值就是那个价值最大的
3. 如果只能装下一个物品,最大价值只能是装下的物品的价值
4. 如果两个都装不下,最大价值就是0
不难发现01背包问题的答案是由背包的大小以及物品的种类多少决定的
那么如何找到递推关系呢?
还是看上面,如果找到了从一个物品递推到第二个物品的关系,就可以以此类推了。
第二个物品只有装和不装两种情况
如果不装,那么就是只有一个物品的情况
如果装了,那么那么这个背包的空间就减少了,同时总的价值也变高了。
那既然装了第二个物品,第一个物品又会怎么样呢?
如果剩余的空间还足够第一个物品装下,那么第一个物品就可以装进背包
如果不够,那么就只能不装了。
比较这两种情况,选择总的价值最大的,这就是答案
现在设函数F(x,y)=最大价值,x为物品种类,y为背包大小
现在有一个物品
1. 如果W[i]>y,无论如何都没办法装下,F(x,y)=F(x-1,y)(这个物品就不考虑了)
2. 如果w[i]<=y,比较装或不装两种情况,选择较大的那种
F(x,y) = max (F(x-1,y),F(x-1,y-w[i])+v[i]),这就是01背包的递归方程
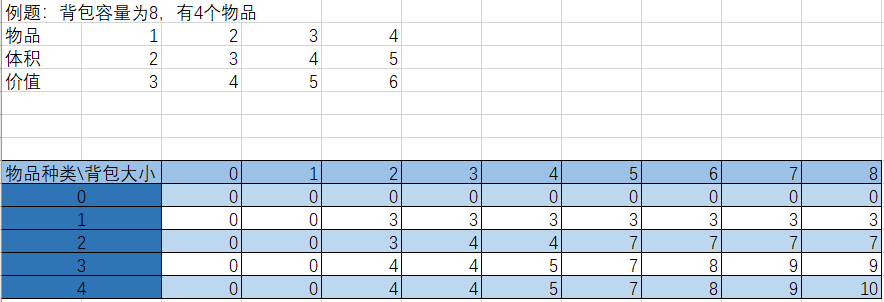
找到了递推方程后,按照递推方程填表,01背包答案就在最后一行最后一列
2. 最长公共子序列问题
给定两个字符串,Sn和Tn
求出这两个字符串最长的公共子序列长度
(子序列:按照从小到大的顺序从原序列中抽出新的元素组成的序列)