作者:龙飞([email protected])
第一部分:兰彻斯特方程
兰彻斯特(Frederick William Lanchester 1868~1946)是英国工程师,流体力学家和运筹学家,也是英国汽车与航空工程先驱者,他于1896年制成英国第一辆汽车。1915年,他在《战斗中的飞机》一文中,首先提出用常微分方程组描述敌对双方兵力消灭过程,定性地说明了集中兵力的原理。这个原理,就是“兰彻斯特方程”(“兰彻斯特”也常被译成“兰切斯特”)。兰彻斯特方程提出两个非常理想化的数学模型:兰彻斯特线性律和兰彻斯特平方律。
1-1:兰彻斯特线性律
兰彻斯特线性律分为第一线性律和第二线性律。
1-1-1:兰彻斯特第一线性律
维基百科对于第一线性律的核心表述是“一个战士每次只能与另外一个敌人战斗。每次只能击杀一个敌人,或者被一个敌人击杀。在作战双方武器相同条件下,战斗结束时剩下的部队数量就简单的是双方部队的数量差——多方多余少方的数量。”
只能有一对一的战斗,换句话说,同一时间,双方只能有相同数量兵力参与战斗。在这种情况下,战损率(战斗损失的兵力数量的变化速度)与双方的兵力数量都没有关系。
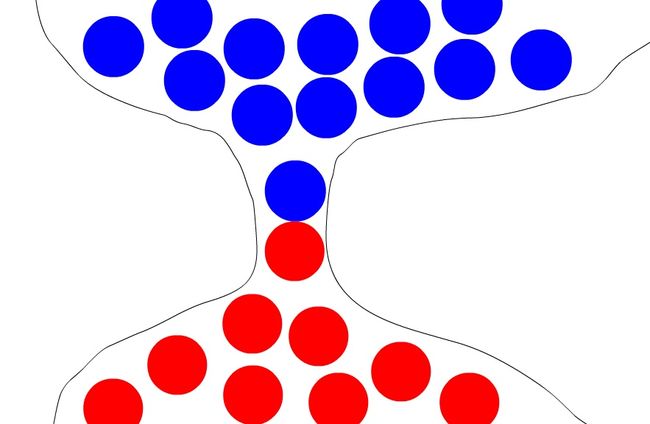
符合第一线性律的真实场景中,“狭路相逢”是最常见的一种:两支部队在有限宽度的路口短兵相接。其中,最简单的一个场景是这个路口只能一对一的战斗,双方都是近战,除了对战的两个单位,其他单位不能参与到战斗中【图01】。两支对战的部队A和B,我们用x表示A随着时间变化的部队数量,y表示B随着时间变化的部队数量;a表示A每个单位的瞬时伤害率(对敌人造成伤害的效率), b表示B每个单位的瞬时伤害率。那么,A的战损率和B的战损率满足以下微分方程:【方程组a】
= -b
= -a
这个方程组通过积分可以得到线性率的“状态方程”
a(- x)=b(- y)【线性率平衡方程】
其中表示A的初始兵力数量,表示B的初始兵力数量。
如果我们说A和B实力相当,那就是说,当A兵力为零的时候B也兵力为零,此时x=y=0,于是:a=b;
这是一个与时间t无关的方程,所以不仅仅在初始兵力下成立,在任何一个瞬间,只要满足:ax=by【兰彻斯特线性律】,我们就可以说A和B战力相等。即,在满足线性律的条件下,部队实力与己方部队数量成正比。
事实上,除了“一对一”的战斗,如果双方参与战斗的兵力数量都是n,n不大于A的兵力总数量x,也不大于B的兵力总数量y,那么描述战损的方程就是:【方程组b】(n≤x, n≤y)
= -bn
= -an
这个方程组依然可以得到线性率的ax=by。
从方程可见,第一线性律所描述的战损率只跟敌方的伤害输出有关,而与己方的伤害输出无关。所以,对于第一线性率更加精确的描述是:如果作战双方总是完全承受相同数量的敌人部队所造成的伤害,那么部队实力与己方部队数量成正比。
维基百科的描述“古代战斗中,在由长矛兵组成的密集阵型之间”的条件,就是在有限宽度路口,或者说是在有限“接触面”情况下的第一线性率【图02】。在这种情况下,只有“第一排”的战士参与到战斗中,后排战士无法输出伤害,直到前排战士被击杀之后补位到第一排。
符合第一线性率的另外一种情况是双方陷入混战,兵力足够分散从而无法相互支援:战斗发生在“捉对厮杀”的两个单位之间【图03】。这种情况可能是短暂的状态,但是在实际条件下,每个单位的移动速度不是足够快,射程也不是足够远——我们说,在有限“协作性”的情况下,战场局面的很多瞬间都是这样的情形。
1-1-2:兰彻斯特第二线性律
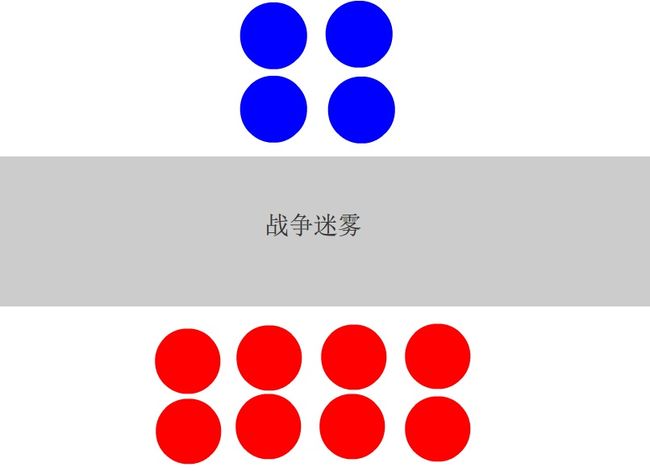
兰彻斯特第二线性率描述了与第一线性率完全不同的场景模型:双方部队在不能精确瞄准的情况下往对方的大概方向的随机位置射击,在双方队列密度和武器都相同的情况下,“人数较多的一方被击中的概率与其击中人数较少一方的次数相平衡”。也就是说,虽然人多的一方单位时间内有更大的伤害输出,但是因为承受伤害的面积更大,所以被击中的概率也更大【图04】。
第二线性率的方程组:【方程组c】
= -byx
= -axy
依然可以推出兰彻斯特线性率的ax=by。(本文所讨论的内容,如果没有特别指出,“兰彻斯特线性率”一般均指“兰彻斯特第一线性率”。)
1-2:兰彻斯特平方律
维基百科对于平方律条件的核心描述是:“部队可以攻击多个目标并受到来自各个方向的伤害”。描述平方律战损的方程组:【方程组d】
= -by
= -ax
如果从方程组看,平方律条件更准确的描述应该是:作战双方总是完全承受所有敌人部队造成的伤害。
积分求得平方律平衡方程:
a(-) = b(-) 【平方率平衡方程】
与线性率一样,最后可以推导出双方战力相等的时候应该有:
=【兰彻斯特平方律】即,在满足平方律的条件下,部队实力与己方部队数量的平方成正比。
符合平方律的经典场景是两只部队彼此进入了对方的有效射程,双方的所有部队都可以攻击到对方。
1-3:兰彻斯特指数
在实际的战斗中,因为每个单位都会占用一定的空间,他们的速度不是足够快,射程也没有足够长。大部分时候,一个单位不仅仅可以攻击到另外一个单位,也不仅仅只能被另外一个单位所攻击;同时也不能攻击到任意敌人单位,且不能被敌人任意单位同时攻击到。在这种情况下,这些单位组成的部队战斗力介于线性率和平方率之间。维基百科中写道,“在现代战争中,常常需要考虑到线性律和平方律在某种程度上同时起作用,通常使用1.5的指数”。本文中把这个指数叫做兰彻斯特指数。
第二部分:攻击先后和临界生命值
兰彻斯特方程的前提假设是:持续输出伤害并且持续受到伤害。在实际的战斗中,如果一个单位因为受到伤害被击杀,那么这个单位就无法再提供伤害输出。如果一个单位受到下一次攻击后就会被击杀,不能做出反击,我们就说这个单位处于临界生命值。
我们考虑线性律中最简单的场景:一对一的战斗。
用A1表示A队的第一个单位,A2表示A队第二个单位,以此类推;A1(1)表示A1的可以承受1次攻击,A1(2)表示A1可以承受2此攻击,以此类推;用A1(1):B1(1)表示可以承受1次攻击的单位A1对抗可以承受1次攻击的单位B1。
最简单的情况A1(1):B1(1),A1和B1都有50%的概率击杀对方,也有50%的概率被对方击杀——取决于谁先发出攻击;而且因为都只能承受1次攻击,所以受到攻击后无法反击。所以结果要么是A1(1):B2(1)(A1先手,B1被击杀后B2顶上),要么是A2(1):B1(1),都有50%的概率。
如果A的每个单位都可以承受2次攻击,那么A1(2):B1(1)的情况就需要逐步分析【图05】。可以看出,完全满足线性律结果的,即2个B单位与1个A单位战力相同的概率只有25%。甚至有极小的概率,1个A单位可以对抗许多B单位(例如,1个A单位对抗6个B单位的概率有3.125%)。
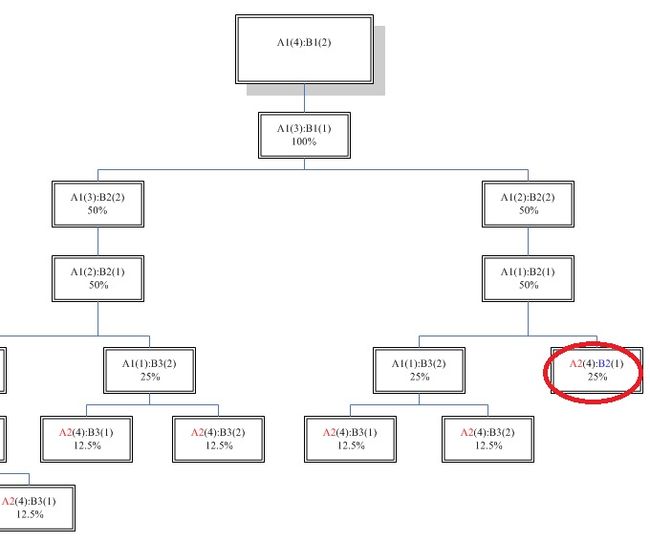
同样,分析A1(4):B1(2)的情况【图06】(A单位质量是B的2倍),满足线性律的概率也只有25%(即);
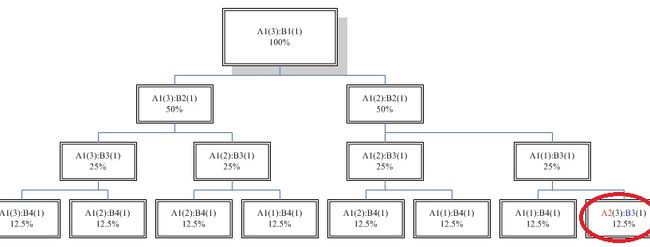
分析A1(3):B1(1)的情况【图07】(A单位质量是B的3倍),满足线性律的概率只有12.5%(即)。
出现这个现象的原因,是因为在受到相同的攻击次数下,质量越高的单位达到临界生命值的比率更小,我们把这种现象叫做质量优势放大。如果考虑到质量优势放大的效应,那么在一些极端情况下会出现比线性律指数更低的情况,也就是说,指数可能介于0到1之间。我们把低于线性律1的兰彻斯特指数(且大于0),叫做次线性指数。
第三部分:先手概率
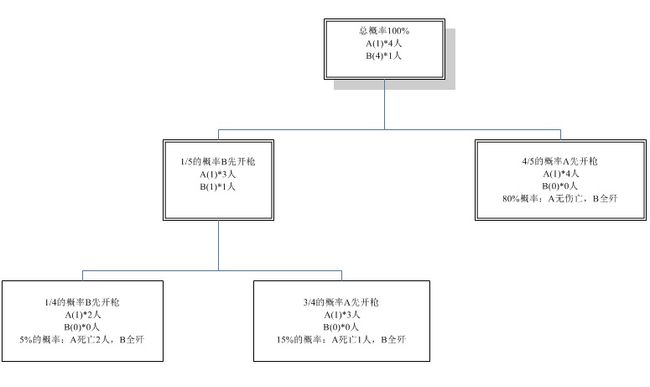
在考虑到攻击先后和临界生命值的基础上,我们再分析一个平方律下的场景:A队有4个单位,每个单位可以承受1次伤害;B队有一个单位,这个单位可以承受4次伤害。分析图【图08】如下:
可见,单位数量多的一方,会有很大的概率(图中是80%的概率)在无伤亡的情况下全歼敌人。这是因为考虑到攻击先后又考虑到被击杀的单位无法反击,那么只有先出手攻击的单位可以造成伤害;而数量越多的一方,先出手攻击的单位数量也多一些。
也就是说,平方律本身就是对数量优势的放大,如果考虑到先手概率,数量优势会被放大得更多,在极端情况下甚至会高于平方律的2。我们把高于平方律2的兰彻斯特指数,叫做超平方指数。
第四部分:韧性与协作性
我们把一个单位承受伤害的能力叫做韧性,把单位能够及时参与输出伤害的能力叫做协作性。通过我们之前的分析,可以得出,兰彻斯特指数介于次线性指数和超平方指数之间,并且有这样的两个结论:
4-1:韧性与协作性都会造成兵力优势放大
韧性会放大单位的质量优势,协作性会放大部队的数量优势。这两种放大效应会叠加在一起,形成部队的兵力优势放大。
4-2:协作性可提升兰彻斯特指数
协作性原本只是让更多的单位及时参与到战斗中,也就是说让战场上更多的单位满足平方律的条件。但是因为有超平方指数的存在,协作性对于兵力数量优势的放大效应会更加明显。这个结论会让战斗场面出现一个有趣且违背直觉的现象:即使兵力接近的两支部队,甚至可能因为随机因素导致一方先减员的,会让这一方完败。协作性越强,这种事件出现的概率越大。
第五部分:战略游戏中的兰彻斯特方程
兵力接近的两支部队发生战斗,结果随机性的一方以非常少的损失全歼了对方——这个“有趣且违背直觉的现象”是游戏中最不愿意看到的情况之一。即便不是这样的极端情况,双方兵力有微小的差距,这种差距也会被兰彻斯特指数放大,表现出来的结果就是,辛辛苦苦发展十几分钟,见面一战就定胜负了:兵力优势放大会让胜利的一方损失很小,而战败的一方几乎全灭。这种情况被玩家戏称为“一波争霸”。
5-1:战棋和回合制
说“违背直觉”,是因为战略游戏并不是从一开始就是这样一战定胜负的。最初的战略游戏,兵力优势放大效应并不明显,这些游戏的兰彻斯特指数较小,偏线性律。
人们自古就对战略游戏有需求,一方面是娱乐的需求,但是更加重要的是,战略游戏在很多元素上模拟了真实的战争——战略游戏以较小的代价(时间成本)在某种程度上满足了人们积累战争博弈经验的需求(而无须真实战争的代价)。在没有电脑和互联网的时候,棋类游戏就是最初的战略游戏。比如说象棋,我们可以把一个回合理解成一个瞬间的“同一时间”:在这个回合中有可能吃掉对方一个棋子也可能没有。如果在n个回合中,A有i次吃子,B有j次吃子,那么A的战力相当于在线性率的基础上乘以,B则乘以,而兰彻斯特指数始终还是1。
电脑上的回合制战棋游戏,一个回合是双方所有单位行动一次的周期。在一个回合中,如果某一方的所有单位都能输出伤害,那么这一个回合之中,这一方的战力满足平方律。实际上,一个回合之中,不一定所有单位都能参与输出;某一方参与输出单位的数量也不一定与另外一方参与输出单位的数量相等。所以,双方的兰彻斯特指数高于线性律的1,而且不一定相等。
由此可见,其实兵力优势放大在回合制战棋类游戏中已经有所体现,但是由于回合制的限制,兵力优势扩大效应并不是在短时间内完成的,而是需要经历多个回合。例如,A1与B1,A2与B2原本在相互捉对厮杀。第一回合中A1击杀了B1,那么A1在回合制的规则下,至少需要到第二回合才能协助A2参与到对B2的攻击中。
5-2:第一代即时战略游戏
在即时战略游戏中,如果A1击杀了B1,在足够速度和足够射程的条件下,A1可以“马上”参与到对A2的协助中。换句话说,A1对于B1的击杀导致B队的减员。在回合制下,在下几个回合之前(A1能协助到A2需要的回合次数),A1和B1都无法参与输出,即A队和B队的兰彻斯特指数都降低了;但是在即时制下,A1可以马上参与到对A2的协助中,B队的兰彻斯特指数因为减员而降低,但是A队并没有降低。所以相对于回合制,即时制的兵力优势放大更加明显。
战棋游戏中每个单位每个回合的行动,都是玩家操作和控制的;而在即时战略游戏中,在时间压力下,如果每个单位都等待玩家具体的操作再做出反应是会让人感觉很古怪的。所以即时战略游戏中,通常每个单位都有一个叫做“警戒范围”的属性,如果有敌人进入这个范围,即便玩家没有发出指令,单位也会去自动攻击。另外,在一场战斗中,如何调整阵型,选择最有效的攻击目标,除了玩家的操作,更多需要AI的计算配合玩家发出的指令来完成。
我们看看在星际1里面被玩家戏称为bug一般的龙骑士寻路AI,甚至在重制版里面为了保持“原汁原味”被保留了下来。当两队在狭窄路口相遇,龙骑士作为射程单位,在敌人刚进入射程的时候就会停止移动开始射击。但在这个时候,敌人并没有进入后排龙骑士的射程。最理想的状态是玩家微操作前排的单位往前再移动一点距离,但是在大部分情况下,普通玩家的手速有限,可能顾及不过来。于是,后排的龙骑士有了奇怪的举动:他们开始往后走,试图“绕”到前面去——即便地图上可能根本无路可绕。
在早期的即时战略游戏中,因为电脑性能限制,以及AI算法的局限性,在没有玩家直接参与微操作的情况下,每个单位的行为显得非常的不智能。这种“笨”可能表现为绕路,也可能表现为发呆,还可能是折线寻路,围杀留口等等,总之,就是每个单位应有的协作性没法完全表现出来。因此,这样的早期战略游戏(我们也称为第一代即时战略游戏),它们相对于战棋游戏有更高的兰彻斯特指数,但是因为手速和AI的限制,很难达到平方律甚至超平方律,这样的游戏对战时兵力消耗较为缓慢和平稳,玩家容易及时止损,比较容易避免出现“一波争霸”的局面。
5-3:第二代即时战略游戏
随着技术与算法的进步,也随着游戏设计经验的积累,即时战略游戏中的AI越来越聪明。以星际争霸2为代表的第二代即时战略游戏中,AI正变得越来越智能和合理。以刚才龙骑士的例子来说,虽然把前排单位前移属于微操作范畴,AI不应该越俎代庖,但是让后排的单位不要乱跑,等待前排单位被击杀后补位却是AI份内的事情。再比如说,把一个单位从密集阵型的部队的一边调动到另外一边,第一代即时战略游戏中那么让这个单位绕路,要么只有手动微操作让挡了路的友军挪动开。而在第二代即时战略游戏中,即便没有微操作,友军也会自动给这个单位让路。
因为AI的进步,让游戏中每个单位协作性可以完全发挥出来,第二代即时战略游戏中的兰彻斯特指数大大提升,可以接近平方律甚至超平方律。我们回顾一下平方律的条件,如果从单方面战力来看,可以表述为:自己所有单位都能参与到战斗的伤害输出。在单位移动速度和射程有限的情况下,最理想的状态莫过于所有单位聚集到一个点上;如果考虑到单位需要占用一定的体积(战场面积),那么能最大化己方战力的方案就是尽量的紧密的阵型,即我们常说的团聚机制。
团聚机制是一把双刃剑:一方面最大化了己方的战力,另外一方面也导致敌人的AOE伤害(Area of Effect,范围伤害)会变得异常强大。当然完全禁止AOE伤害也是不明知的,如果没有AOE伤害的制衡,那么较高的兰彻斯特指数会让所有战斗靠无悬念的胜者损失极小而败者全灭。所以,第二代即时战略游戏除了削弱AOE伤害,还需要更多的机制来制衡高兰彻斯特指数造成的兵力优势放大的影响。
5-4:战略游戏的需求
一场势均力敌的比赛才是精彩的比赛。如果比赛刚开始不久就可以断定胜负,或者在比赛之中呈现出一边倒的局面,这不仅让观看者毫无悬念,还会让劣势方带着无望的挫败感消极比赛,甚至让优势方缺少乐趣和成就感。
传统的战略游戏往往模拟了一个发展的过程:玩家的兵力从无到有,从少到多。玩家历经十几分钟甚至几十分钟的发展(一般竞技游戏会控制一场游戏的总时间,而单机PvE的游戏可能需要更长的发展周期),终于组织起一支足够强大的部队,结果双方部队遭遇,在几分钟甚至几十秒内就胜负已定,而且在兰彻斯特指数兵力优势放大的影响下,往往获胜方以大优势取胜。这样,一场战斗失败的一方,几乎没有翻盘的可能。这不是玩家希望看到的局面,也不是游戏设计者希望看到的局面。
我们希望在战略游戏中,对抗的双方优势和劣势都是慢慢积累起来的,而且因为决策或者操作,优势可以失去,劣势也可以挽回。我们希望每一场战斗都是势均力敌的,而且希望能多有几场战斗——毕竟对于大部分玩家来说,相对于发展,激烈的正面交锋显得更加有趣。于是在正面战场上,有了兵种相克和范围伤害(AOE)等设计来制衡兰彻斯特指数兵力优势放大。增加了防守的优势如狭窄地形(降低兰彻斯特指数),斜坡(视野与命中率),炮台(比兵种单位性价比更高)等。在发展策略上,制定了针对性的数学模型从资源和经济上来制衡。
比如,在星际1中,因为兰彻斯特指数不高,每个种族可以根据自身特色制定出不同的经济发展模型;而在星际2中,因为兰彻斯特指数的提升,三个种族的经济模型都非常接近——在满人口的时候都是70左右的农民,资源收益速度都差不多。因为即使相当实力的兵力对战也充满着极大的不确定性,星际2的经济模型让一场战斗的损失可以尽快弥补回来——只要经济足够好。而在魔兽争霸3中,总人口的限制和维护费的限制,让即便是5个农民的人口占用也显得捉襟见肘。魔兽3的经济模型试图让对战双方的人口都控制在战力接近的水平上,经济也控制在差不多收入的水平上,以此让玩家把更多的精力和操作放在正面战场上。
总之,兰彻斯特指数兵力优势放大是战略游戏需要考虑到的一个基本原理。低兰彻斯特指数的战略游戏有着自己的乐趣和魅力,就像象棋和国际象棋依然吸引着许多爱好者。但是随着技术和算法的进步,高兰彻斯特指数的即时战略类游戏更加符合人们对于真实战斗模拟的预期——特别是即时战略游戏主要表现的局部正面战场。当我们抱怨像星际2这样的游戏中,往往双方兵力抱团游走,谁也不敢轻易出手,一旦交火似乎操作无用,甚至“双手离开键盘”效果更佳的时候,只有多思考,更加深入的去分析背后的原理,才能找到去适应技术进步的合理和科学的设计方案。