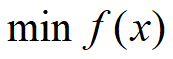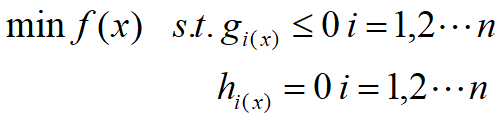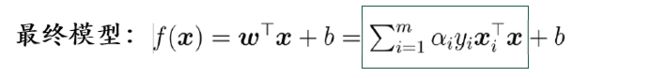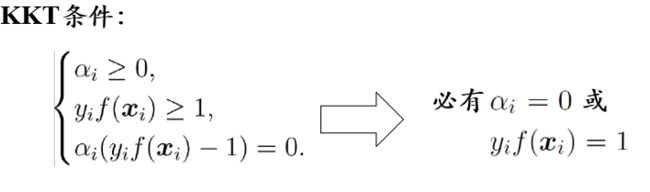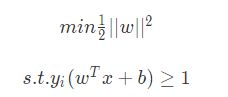二、对偶问题
1、优化问题的类型
(1)无约束优化问题:
求解方法:求取函数f(x)的导数,然后令其为零,可以求得候选最优值,再在这些候选值中验证;如果是凸函数,可以保证是最优解。
(2)有等式约束的优化问题:
即把等式约束hi(x)用一个系数与f(x)写为一个式子,称为拉格朗日函数,而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导,令其为零,可以求得候选值集合,然后验证求得最优值。
(3)有不等式约束的优化问题:
把所有的等式约束、不等式约束与f(x)写成一个式子,这个式子也叫拉格朗日函数,系数也称为拉格朗日乘子。
通过一些条件,可以求出最优值的必要条件,这个条件就称为 KKT条件。
2、对偶问题
对SVM基本型使用拉格朗日乘子可得其“对偶问题”(dual problem)。
求解步骤:
解的稀疏性: 训练完成后 , 最终模型仅与支持向量有关
支持向量机(Support Vector Machine, SVM) 因此而得名
3、硬间隔与软间隔
硬间隔:不允许样本分类错误
软间隔:允许一定量的样本分类错误
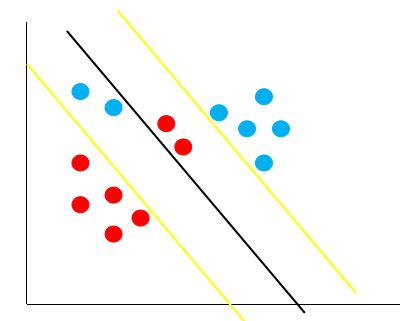
假如现在有一份数据分布如下图:
按照线性可分支持向量机的思想,黄色的线就是最佳的决策边界。很明显,这条线的泛化性不是很好,造成这样结果的原因就是数据中存在着异常点,那么如何解决这个问题呢,支持向量机引入了软间隔最大化的方法来解决。
所谓的软间隔,是相对于硬间隔说的,即之前我们所讲的支持向量机学习方法。回顾下硬间隔最大化的条件:
接着我们再看如何可以软间隔最大化呢?SVM 对训练集里面的每个样本 ( xi , yi ) 引入了一个松弛变量 xi ≥ 0 , 使函数间隔加上松弛变量大于等于 1 ,也就是说:
对比硬间隔最大化,可以看到我们对样本到超平面的函数距离的要求放松了,之前是一定要大于等于 1 ,现在只需要加上一个大于等于 0 的松弛变量能大于等于 1 就可以了。也就是允许支持向量机在一些样本上出错,如下图:
基本思路: