背景:DC竞赛比赛项目,运用回归模型进行房价预测。
数据:主要包括2014年5月至2015年5月美国King County的房屋销售价格以及房屋的基本信息。
目标:算法通过计算平均预测误差来衡量回归模型的优劣。平均预测误差越小,说明回归模型越好。
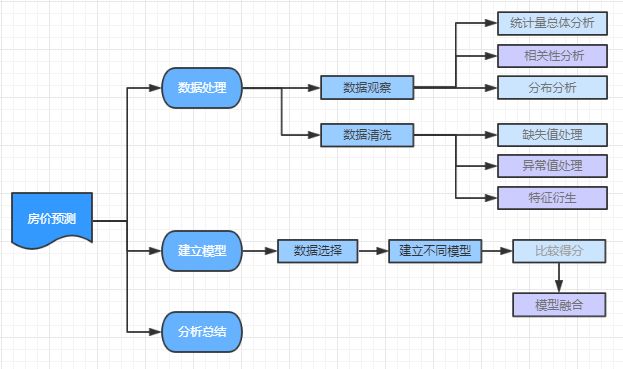
流程图:
【一】数据观测
1>读取数据
IO = r'C:\Users\Administrator\Desktop\kc_train.csv'
def read_csv_data(IO):
with open(IO) as f:
reader = csv.reader(f)
data = list(reader)
print("Done")
data_numpy = np.zeros((len(data), len(data[0])))
for i, sample_list in enumerate(data):
print(i)
for index, iterm in enumerate(sample_list):
if index==3 or index==12 or index==13:
data_numpy[i, index] = str2float(iterm)
else:
data_numpy[i, index] = float(iterm)
import h5py
f = h5py.File("kc_train.hdf5", "w")
f.create_dataset(name="data_set", data=data_numpy)
f.close()
return data_numpy
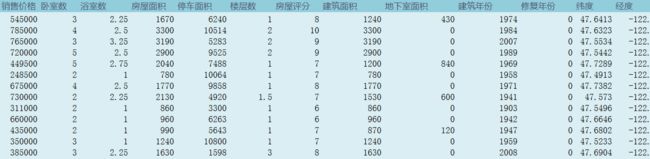
data = pd.read_csv(r'C:\Users\John\Desktop\DCastle\ML_DL\美国King County房价预测训练赛\kc_train.csv', header=None, names=['销售日期', '销售价格', '卧室数', '浴室数', '房屋面积', '停车面积', '楼层数', '房屋评分', '建筑面积', '地下室面积', '建筑年份','修复年份', '纬度', '经度'])
2>观察数据
data['销售价格'].describe()
plt.subplots(figsize=(12,9))
sns.distplot(data['销售价格'])
查看偏度与峰度
print("Skewness: %f" %data['销售价格'].skew()) #偏度
print("Kurtosis: %f" %data['销售价格'].kurt()) #峰度
Skewness: 3.898737
Kurtosis: 29.356202
3>相关性分析
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
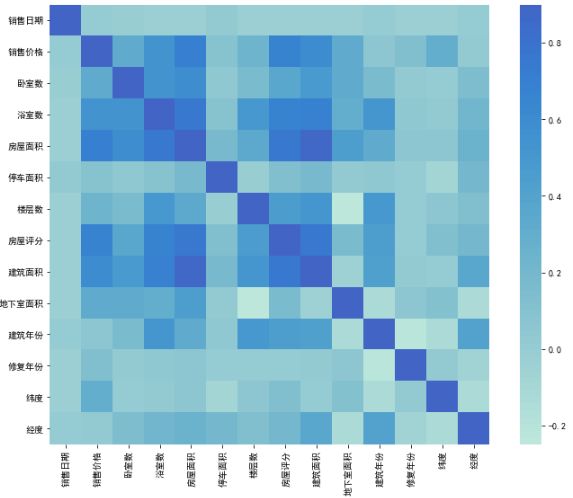
corrmat = data.corr()
plt.subplots(figsize=(12,9))
sns.heatmap(corrmat, vmax=0.9, square=True,center=2.0)
相关性前10位的相关性分析
k = 10
plt.figure(figsize=(12,9))
cols = corrmat.nlargest(k, '销售价格')['销售价格'].index
cm = np.corrcoef(data[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
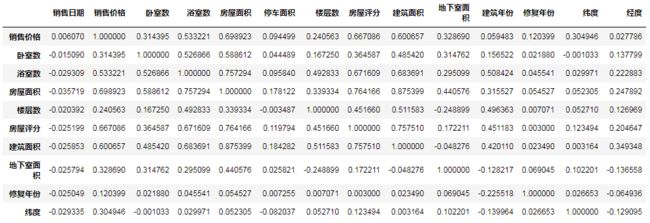
Corr = data.corr()
Corr[Corr['销售价格']>0.1]
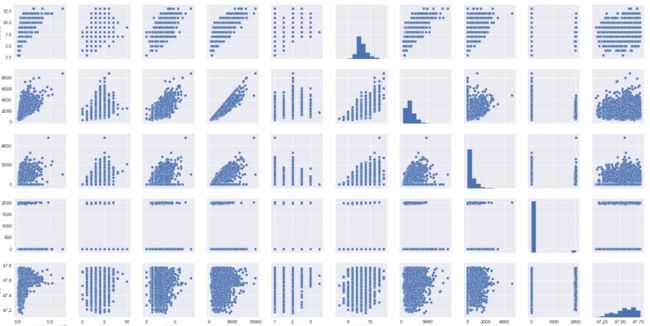
绘制维度的散点图
sns.set(font='SimHei)
cols = ['销售价格','卧室数','浴室数','房屋面积','楼层数','房屋评分','建筑面积','地下室面积','修复年份','纬度']
sns.pairplot(data[cols], size = 2.5)
plt.show();
【二】数据清洗
将各维度数据分析,删除明显的异常值。
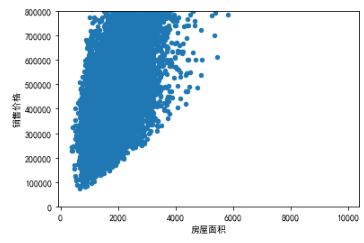
1>连续变量
data1 = pd.concat([data['销售价格'], data['房屋面积']], axis=1)
data1.plot.scatter(x='房屋面积', y='销售价格', ylim=(0,800000));
fig = plt.figure()
sns.distplot(data['房屋面积']);
from scipy import stats
fig = plt.figure()
res = stats.probplot(data['房屋面积'], plot=plt)
同理观测连续变量后删除差距过大的异常值
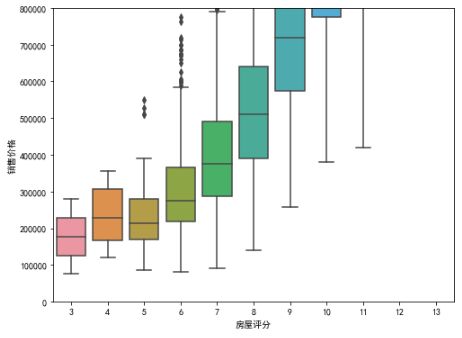
2>离散变量
data2 = pd.concat([data['销售价格'], data['房屋评分']], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x='房屋评分', y="销售价格", data=data2)
fig.axis(ymin=0, ymax=800000);
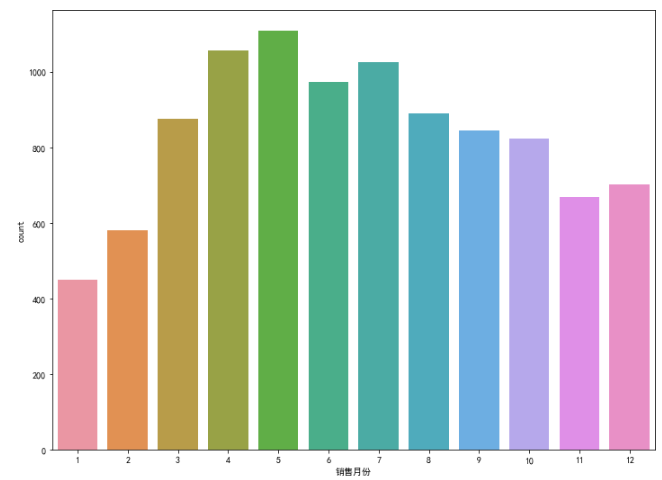
3>特征变量
将时间处理成月份生成新的维度。
print(data.groupby('销售月份')['销售价格'].count()) #月份统计
plt.subplots(figsize=(12,9))
sns.countplot(x='销售月份',data=data)
4>空值
本次项目中数据较为完整,没有空值存在,无需删除。
【三】建立模型
本次项目中选择随机森林,逻辑回归,SVM等。
1>数据选择
训练集,测试集比例为7:3。
def Data(IO):
X=pd.read_excel(IO)
Y = X['销售价格']
X= X.drop('销售价格'],axis = 1)
X_train, X_test, y_train, y_test = \
cross_validation.train_test_split( X, Y, test_size=0.3, random_state=0)
return (X_train, X_test, y_train, y_test)
2>模型建立
def RF(X_train, X_test, y_train, y_test): #随机森林
from sklearn.ensemble import RandomForestClassifier
model= RandomForestClassifier(n_estimators=100)
model.fit(X_train, y_train)
predicted= model.predict(X_test)
score = accuracy_score(y_test, predicted)
return (score)
def LOR(X_train, X_test, y_train, y_test): #逻辑回归
from sklearn.linear_model import LogisticRegression
lor = LogisticRegression(penalty='l1',C=100,multi_class='ovr')
lor.fit(X_train, y_train)
predicted= lor.predict(X_test)
score = accuracy_score(y_test, predicted)
return (score)
def Svm(X_train, X_test, y_train, y_test): #支持向量机
from sklearn import svm
model = svm.SVC(kernel='rbf')
model.fit(X_train, y_train)
predicted= model.predict(X_test)
score = accuracy_score(y_test, predicted)
return (score)
def LR(X_train, X_test, y_train, y_test): #线性回归
from sklearn.linear_model import LinearRegression
LR = LinearRegression()
LR.fit(X_train, y_train)
predicted = LR.predict(X_test)
score = accuracy_score(y_test, predicted)
return ( score,LR.intercept_,LR.coef_)
3>模型融合
根据模型得分尝试不同比例的融合效果
eg:
result1 = 0.7*RF + 0.25*LOR+0.05*LR
result2 = 0.7*RF + 0.1*LOR+0.2*LR
result3 = 0.7*Svm + 0.25*LOR+0.2*LR
result4 = 0.7*Svm + 0.1*LOR+0.2*LR
最后比较得出得分较高的模型,选择上传。
【四】比对总结
本次数据较为完整,数据清洗部分较为轻松。
给定的维度较少,根据经验需要做的特征工程较多。
比较而言,随机森林的预测效果最优,SVM调参后有性能提升的空间。
感谢江流静一的支持:
https://blog.csdn.net/u012063773