杨辉三角与绳子问题

杨辉三角与绳子问题

首先我们先来回忆一下杨辉三角, 即如下结构:

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1

该结构是怎么得到的呢? 假设我们现在有一个n行n列大小的grid, 那么在假设现在我们在第i行第j列。 那么该位置的值, 即:

看到这个就很容易回想起动态规划中memorization, 很显然, grid[i][j]的值仅仅取决于其上一层的grid[i-1][:]的值, 那么我们就可以利用动态规划中的空间压缩, 舍去grid, 只用一个数组保留上一行的状态。

其实我们还可以更进一步将上一层状态和本层状态压缩成一个数组, 就省去了用两个数组的麻烦。 Talk is cheap, show me the code:

#include 
#include  
using std::cout;
using std::endl;
using std::vector;

int main()  
{   
    int step=10;
    vector temp(step,1);
    for(int i=0;i0;j--){ //切记此处要从后往前更新, 如果j是从前往后更新那么每次都使用的更新后的状态就错了
            temp[j]+=temp[j-1];  
        }
        for(int j=0;j<=i;j++){
            cout<

那既然我们已经了解了杨辉三角, 我们现在来看一道题:

现在有一根长为 n 的绳子, 要分成 m 段, 请问有多少种分法。假如n=3, m=2, 那么答案就是 12和21两个; 若n=4, m=2, 那么答案就是13,22,31为3。

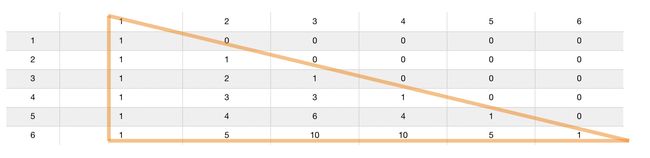
如果碰到这种问题一时想不出递推公式该怎么写的话, 不妨先将二维矩阵grid画出来, 即(每一列代表当绳子长度n为1,2,3,4,5,6时 ; 每一行代表当需要分的段数m为1,2,3,4,5时, grid[i][j]代表当绳子长度为i而需要分j段时, 不同的分段方式 ):

90C1B6951ADB89C13D385492F7589DD9.jpg

当我们留意上图中相同颜色的格子括起来的数后, 不难得到通项公式, 通项公式为:

grid[i][j]=grid[i-1][j-1]+grid[i][j-1]

换句话说, 一个长度为n的绳子被分成m段的所有可能等同于一个长度为n-1被分成m和m-1段的所有可能相加。

你可能会说, 这看上去像杨辉三角但是不是杨辉三角啊, 杨辉三角是

grid[i][j] = grid[i-1][j] + grid[i-1][j-1]

那我们如果把上面那个图竖过来呢, 即每一行代表绳子长度n为1,2,3,4,5时, 每一列代表需要分的段数m为1,2,3,4,5, 那么此时就有:

B910BF918496D4B33B02C767D4BE85DE.jpg

很显然, 此时是满足杨辉三角的定义的, 通项公式即:

grid[i][j] = grid[i-1][j] + grid[i-1][j-1]

代码为:

int split_rope(int n,int m){
    if(!m||!n){
        return 0;
    }
    if(m>=n){
        return n/m; //当n==m时返回1, 否则返回0
    }
    vector result(n,1);  //用n个1来填充vector
    for(int i=0;i0;j--){ //此处j要大于0, 确保下面的result[j-1]不会取到负数的下标
            result[j]+=result[j-1];
        }
    }
    return result[m-1]; //注意m代表分为m段, 而返回值的下标是从0开始的, 所以此处要m-1
}

给定一根长度为n绳子，请把绳子剪成m段(m、n都是整数，n>1并且m≥1), 求出这m段绳子的长度的乘积最大是多少。注意, 要剪成m段的m是由你自己来决定的, 你要遍历所有可能, 找出能使乘积最大的段数m, 并返回最大乘积。

这道题跟上面那道是不一样的, 这道题不再考虑元素间的顺序。举个例子, 假如n=3, m=2那么, 很显然 12 和 21 在上面那道题中是算两种状态。而在此处, 因为 12 和 21 乘积结果是一样的, 在这道题中这两者是同一种状态。既然两者同属一个状态, 那么就使得递归求解成为了可能。即
说个题外话, 此处如果把换成就是卡特兰数的递推公式了。那么我们此时可以采用自下而上解决问题, 代码就不额外写了, 直接用网上广为流传的代码吧(https://blog.csdn.net/shu15121856/article/details/82384171), 只需要传入一个n用来指代所需要切割的绳子长度即可:

#include
using namespace std;

//输入绳子的长度,输出最大乘积 
int maxProductAfterCutting_solution1(int length) {
    if(length < 2)//因为要求长度n>1,所以这里返回0表示输入非法 
        return 0;
    if(length == 2)//长度为2时,因为要求剪下段数m>1,所以最大是1x1=1 
        return 1;
    if(length == 3)//长度为3时,因为要求剪下段数m>1,所以最大是1x2=2 
        return 2;

    //运行至此,说明绳子的长度是>3的,这之后0/1/2/3这种子问题最大就是其自身长度
    //而不再需要考虑剪一刀的问题,因为它们剪一刀没有不剪来的收益高
    //而在当下这么长的绳子上剪过才可能生成0/1/2/3这种长度的绳子,它们不需要再减
    //所以下面的表中可以看到它们作为子问题的值和上面实际返回的是不一样的 

    //在表中先打上子绳子的最大乘积 
    int* products = new int[length + 1];
    products[0] = 0;
    products[1] = 1;
    products[2] = 2;
    products[3] = 3;//到3为止都是不剪最好 

    int max = 0;//用于记录最大乘积 
    //对于4以上的情况,每次循环要求f(i) 
    for(int i = 4; i <= length; ++i) {
        max = 0;//每次将最大乘积清空
        //因为要计算f(j)乘以f(i-j)的最大值,j超过i的一半时是重复计算
        //所以只需要考虑j不超过i的一半的情况 
        for(int j = 1; j <= i / 2; ++j) {
            //计算f(j)乘以f(i-j)
            int product = products[j] * products[i - j];
            //如果比当前找到的还大 
            if(max < product)
                max = product;//就把最大值更新 
        }
        //这里是循环无关的,书上在for里面,我把它提出来 
        products[i] = max;//最终,更新表中的f(i)=max(f(j)·f(i-j))
    }
    //循环结束后,所求的f(length)也就求出来了 
    max = products[length];//将其记录下来以在销毁后能返回 
    delete[] products;//销毁打表的辅助空间 
    return max; 
}

int main(){
    cout<

除此之外, 还可用贪心算法解决。

当n>=5时，3(n−3)>=2(n−2)且只在n取5时取等号，且它们都大于n，所以应把绳子剪成尽量多的3，让剩下的都是2这样的组合。

书上言尽于此，我想了下如果剪成其它大小的会不会更好。如果剪成4，那么4=2×2=2+2就还是和剪成两个2一样，如果剪成5，那么5还能继续剪剪成3和2，往后也是一样。试想更大的数，比如15，得到一段15以后不剪是不可能的，因为前面说了这时候3(n−3)>2(n−2)>n，那么剪成更小的段，只要不小于5就一定满足这个就要继续减，如果比5小，从1~4的情况都想过了，4是不用管的或者剪成两个2，3就保留，2也保留，1不要出现。

#include
using namespace std;

//输入绳子的长度,输出最大乘积 
int maxProductAfterCutting_solution2(int length) {
    if(length < 2)//因为要求长度n>1,所以这里返回0表示输入非法 
        return 0;
    if(length == 2)//长度为2时,因为要求剪下段数m>1,所以最大是1x1=1 
        return 1;
    if(length == 3)//长度为3时,因为要求剪下段数m>1,所以最大是1x2=2 
        return 2;

    //尽可能多地减去长度为3的绳子段,这里是计算一下能减出多少个3 
    int timesOf3 = length / 3;

    //当绳子最后剩下的长度为4的时候,不能再剪去长度为3的绳子段。
    //此时更好的方法是把绳子剪成长度为2的两段,因为2*2>3*1。
    if(length - timesOf3 * 3 == 1)//如果最后只剩一个1 
        timesOf3 -= 1;//就要留下一个3 

    //保证剩下的一定是4或者2或者0,计算一下能剪出几个2来(只有2/1/0三种情况) 
    int timesOf2 = (length - timesOf3 * 3) / 2;

    //3的多少个3次幂,再乘以2的多少个2次幂,就是贪心选择的最优解 
    return (int) (pow(3, timesOf3)) * (int) (pow(2, timesOf2));
}

int main(){
    cout<