数据结构…本系列旨在对基础算法进行记录和学习,为了之后的面试一个弥补~~
本系列不是科普文,是为了找工作快速拾遗系列.
快速浏览,不会把学过的东西忘记~~
//申明一下：这篇文章的图片主要来自“小甲鱼数据结构”
//有些人说小甲鱼不专业，这个肯定有的，代码不规范也肯定有的。
//主要学习“图”的思想，快速的进行学习，其它不做讨论
//在这里感谢`http://www.fishc.org/`
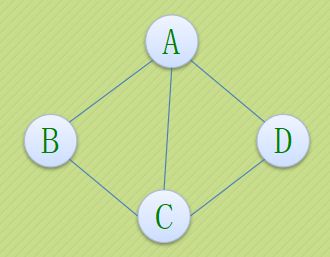
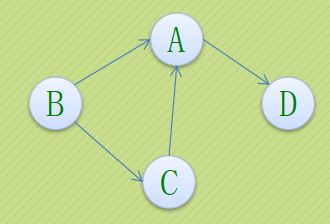
1.图种类
- 无向无权图
- 无向有权图
- 有向无权图
- 有向有权图
- ......其它的没遇到过
无向无权图
有向无权图
无向有权图
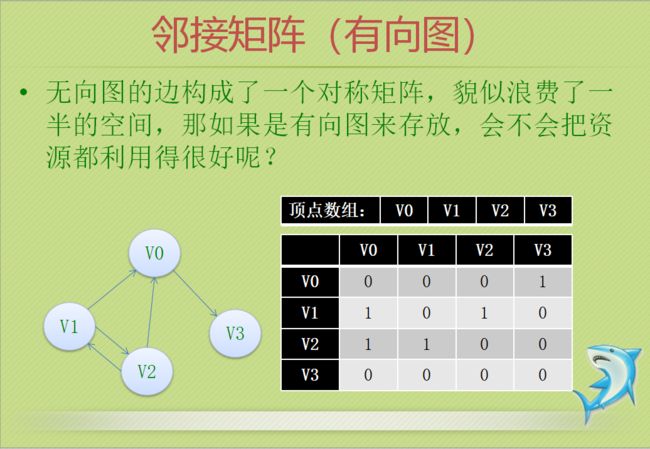
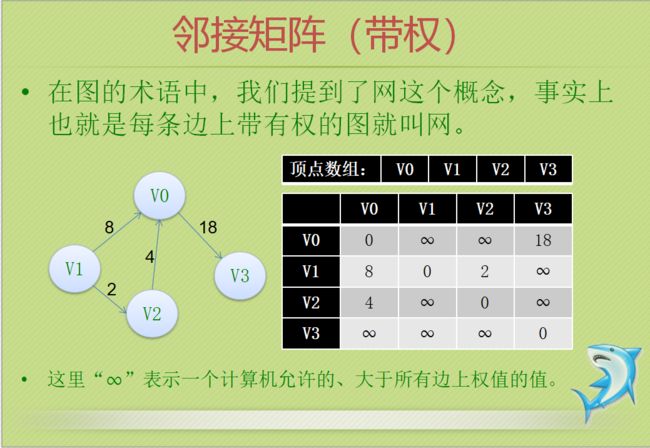
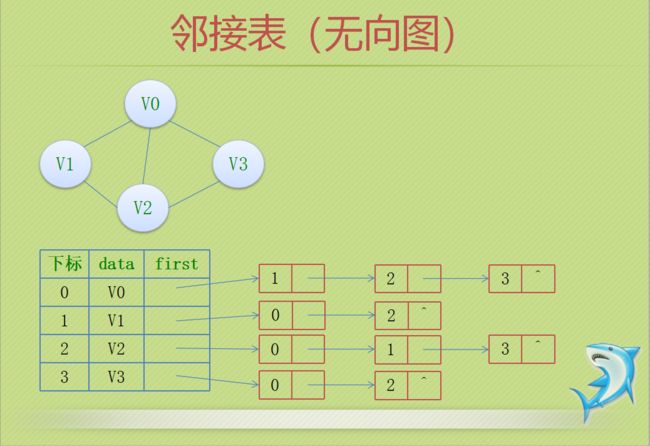
2.图的表示方法
邻接矩阵-无向图
邻接矩阵-有向图
邻接矩阵-带权图
邻接表-无向图
邻接表-有向图
邻接表-带权图
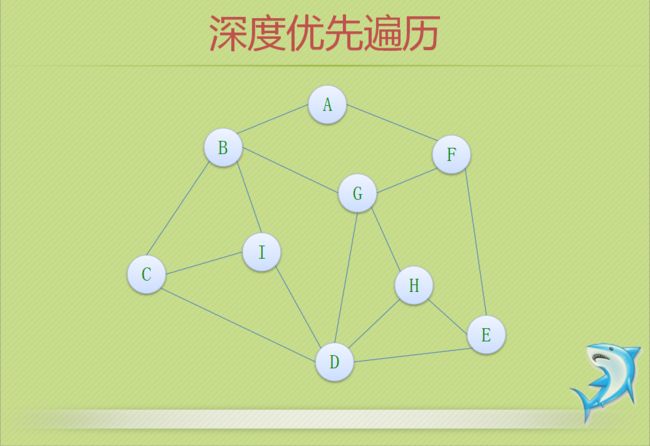
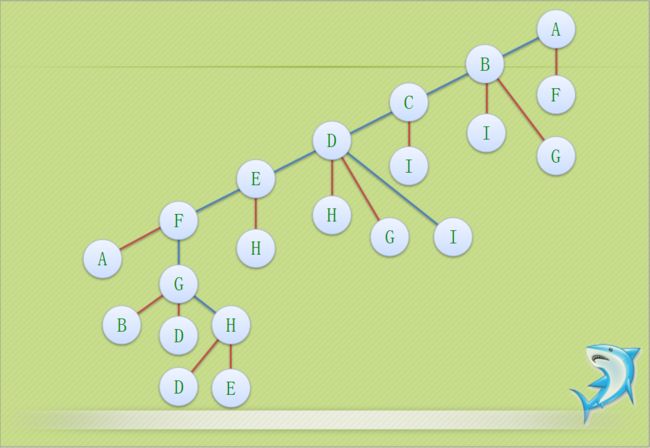
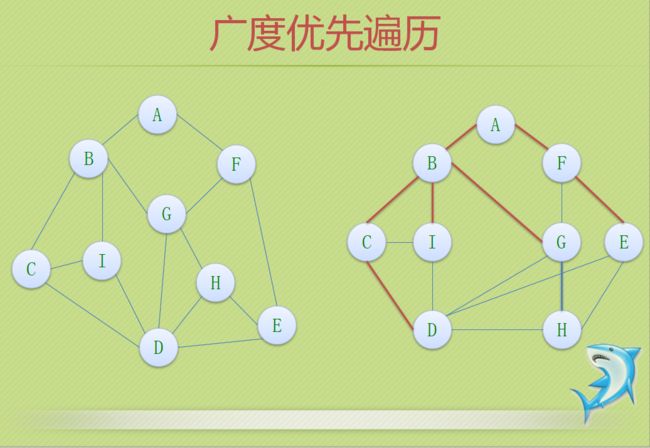
3.遍历方式
深度优先DFS
深度优先具体过程图
广度优先BFS
广度优先具体图
4.最小生成树
Prim算法
操作流程图
后面还有很多“最小生成树的算法”，时间来不及了，大概了解一下，以后再补充......
5.代码实现
//*******邻接矩阵**********//
#define _CRT_SECURE_NO_WARNINGS
#include
using namespace std;
#define MAXVEX 100 //顶点数
#define INFINITY 65535 //用65535来代表无穷大
typedef struct
{
char vexs[MAXVEX]; //顶点表
int arc[MAXVEX][MAXVEX]; //邻接矩阵
int numVertexes, numEdges; //图中当前的顶点数和边数
}MGraph;
//建立无向网络的邻接矩阵
void CreateMGraph(MGraph *G)
{
int i, j, k, w;
printf("请输入顶点数和边数：\n");
scanf("%d,%d", &G->numVertexes, &G->numEdges);
printf("请输入顶点标记（如：A,B,C等）：\n");
for (i = 0; i < G->numVertexes; i++)
{
//scanf("%c", &G->vexs[i]);
cin >> &G->vexs[i];
}
for (size_t i = 0; i < G->numVertexes; i++)
{
for (size_t j = 0; j < G->numVertexes; j++)
{
G->arc[i][j] = INFINITY;
}
}
for (size_t k = 0; k < G->numEdges; k++)
{
printf("请输入边（Vi，Vj）上的下标i，下表j和对应的权w：\n");
scanf("%d,%d,%D", &i, &j,&w);
G->arc[i][j] = w;
G->arc[j][i] = G->arc[i][j];
}
}
int main()
{
MGraph test;
CreateMGraph(&test);
return 0;
}
//*****邻接表*********//
#define _CRT_SECURE_NO_WARNINGS
#include
using namespace std;
#define MAXVEX 100
typedef struct EdgeNode // 边表结点
{
int adjvex; // 邻接点域，存储该顶点对应的下标
int weight; // 用于存储权值，对于非网图可以不需要
struct EdgeNode *next; // 链域，指向下一个邻接点
} EdgeNode;
typedef struct VertexNode // 顶点表结点
{
char data; // 顶点域，存储顶点信息
EdgeNode *firstEdge; // 边表头指针
} VertexNode, AdjList[MAXVEX];
typedef struct
{
AdjList adjList;
int numVertexes, numEdges; // 图中当前顶点数和边数
} GraphAdjList;
// 建立图的邻接表结构
void CreateALGraph(GraphAdjList *G)
{
int i, j, k;
EdgeNode *e;
printf("请输入顶点数和边数：\n");
scanf("%d %d", &G->numVertexes, &G->numEdges);
// 读取顶点信息，建立顶点表
for (i = 0; i < G->numVertexes; i++)
{
//scanf("%c", &G->adjList[i].data);
cin >> &G->adjList[i].data;
G->adjList[i].firstEdge = NULL; // 初始化置为空表
}
for (k = 0; k < G->numEdges; k++)
{
printf("请输入边(Vi,Vj)上的顶点序号：\n");
scanf("%d %d", &i, &j);
e = (EdgeNode *)malloc(sizeof(EdgeNode));
e->adjvex = j; // 邻接序号为j
e->next = G->adjList[i].firstEdge;
G->adjList[i].firstEdge = e;
e = (EdgeNode *)malloc(sizeof(EdgeNode));
e->adjvex = i; // 邻接序号为i
e->next = G->adjList[j].firstEdge;
G->adjList[j].firstEdge = e;
}
}
int main()
{
GraphAdjList test;
CreateALGraph(&test);
return 0;
}
//*****邻接表的深度有限递归算法*****//
#define TRUE 1
#define FALSE 0
#define MAX 256
typedef int Boolean; // 这里我们定义Boolean为布尔类型，其值为TRUE或FALSE
Boolean visited[MAX]; // 访问标志的数组
void DFS(GraphAdjList GL, int i)
{
EdgeNode *p;
visited[i] = TRUE;
printf("%c " GL->adjList[i].data);
p = GL->adjList[i].firstEdge;
while(p)
{
if( !visited[p->adjvex] )
{//判断是否进入下一个节点
DFS(GL, p->adjvex);
}
p = p->next;//遍历完自身连接的节点
}
}
// 邻接表的深度遍历操作
void DFSTraverse(GraphAdjList GL)
{
int i;
for( i=0; i < GL->numVertexes; i++ )
{
visited[i] = FALSE; // 初始化所有顶点状态都是未访问过状态
}
for( i=0; i < GL->numVertexes; i++ )
{//访问每一个节点
if( !visited[i] ) // 若是连通图，只会执行一次
{
DFS(GL, i);//以一个节点为起点去寻找其它节点
}
}
}
// ****邻接矩阵的深度有限递归算法****//
#define TRUE 1
#define FALSE 0
#define MAX 256
typedef int Boolean; // 这里我们定义Boolean为布尔类型，其值为TRUE或FALSE
Boolean visited[MAX]; // 访问标志的数组
void DFS(MGraph G, int i)
{
int j;
visited[j] = TRUE; // 访问过的顶点设置为TRUE
printf("%c ", G.vexs[i]); // 打印顶点
for( j=0; j < G.numVertexes; j++ )
{
if( G.arc[i][j]==1 && !visited[j] )
{
DFS(G, j); // 对为访问的邻接顶点递归调用
}
}
}
// 邻接矩阵的深度遍历操作
void DFSTraverse(MGraph G)
{
int i;
for( i=0; i < G.numVertexes; i++ )
{
visited[i] = FALSE; // 初始化所有顶点状态都是未访问过状态
}
for( i=0; i < G.numVertexes; i++ )
{
if( !visited[i] ) // 若是连通图，只会执行一次
{
DFS(G, i);
}
}
}
// *****邻接矩阵的广度遍历算法*****//
void BFSTraverse(MGraph G)
{
int i, j;
Queue Q;
for( i=0; i < G.numVertexes; i++ )
{//初始化“是否访问”标志位
visited[i] = FALSE;
}
initQueue( &Q );//初始化队列，先进先出
for( i=0; i < G.numVertexes; i++ )
{//遍历全部节点
if( !visited[i] )
{
printf("%c ", G.vex[i]);
visited[i] = TRUE;
EnQueue(&Q, i);//没有访问，入队列
while( !QueueEmpty(Q) )
{//队列不为空，沿着一个节点一直找下去
DeQueue(&Q, &i);//当前节点先出队列，出的节点不一定是i，而是先进去的那个节点
for( j=0; j < G.numVertexes; j++ )
{//当前节点找到其它节点入队列
if( G.art[i][j]==1 && !visited[j] )
{//满足条件入队
printf("%c ", G.vex[j]);
visited[j] = TRUE;
EnQueue(&Q, j);
}
}
}
}
}
}
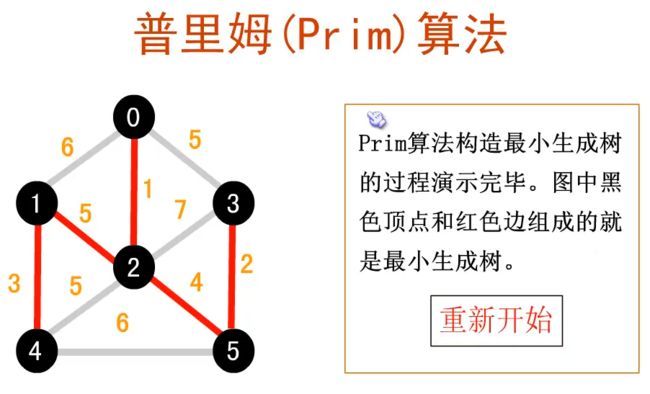
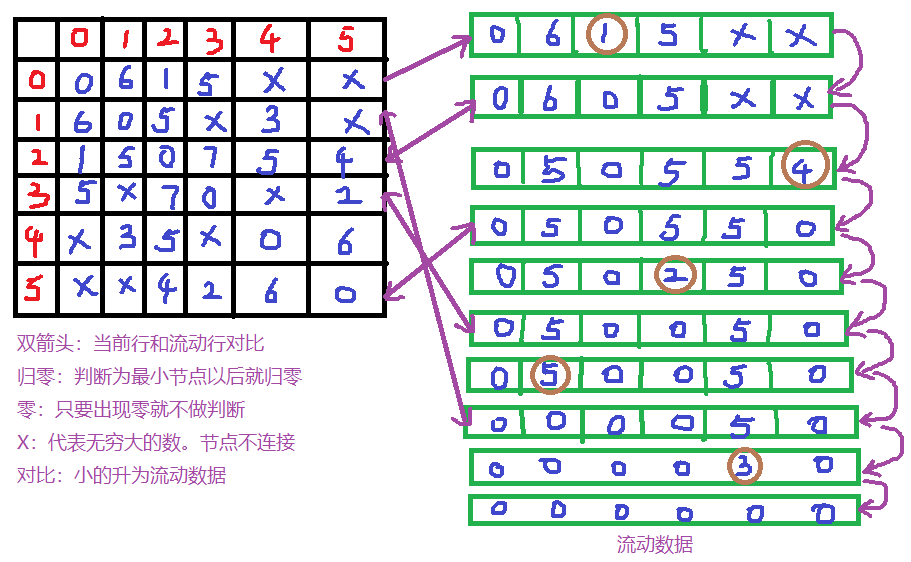
// Prim算法生成最小生成树
void MiniSpanTree_Prim(MGraph G)
{
int min, i, j, k;
int adjvex[MAXVEX]; // 保存相关顶点下标
int lowcost[MAXVEX]; // 保存相关顶点间边的权值
lowcost[0] = 0; // V0作为最小生成树的根开始遍历，权值为0
adjvex[0] = 0; // V0第一个加入
// 初始化操作
for( i=1; i < G.numVertexes; i++ )
{
lowcost[i] = G.arc[0][i]; // 将邻接矩阵第0行所有权值先加入数组
adjvex[i] = 0; // 初始化全部先为V0的下标
}
// 真正构造最小生成树的过程
for( i=1; i < G.numVertexes; i++ )
{
min = INFINITY; // 初始化最小权值为65535等不可能数值
j = 1;
k = 0;
// 遍历全部顶点
while( j < G.numVertexes )
{
// 找出lowcost数组已存储的最小权值
if( lowcost[j]!=0 && lowcost[j] < min )
{
min = lowcost[j];
k = j; // 将发现的最小权值的下标存入k，以待使用。
}
j++;
}
// 打印当前顶点边中权值最小的边
printf("(%d,%d)", adjvex[k], k);
lowcost[k] = 0; // 将当前顶点的权值设置为0，表示此顶点已经完成任务，进行下一个顶点的遍历
// 邻接矩阵k行逐个遍历全部顶点
for( j=1; j < G.numVertexes; j++ )
{
if( lowcost[j]!=0 && G.arc[k][j] < lowcost[j] )
{
lowcost[j] = G.arc[k][j];
adjvex[j] = k;
}
}
}
}
参考资料:
小甲鱼数据结构
B站视频地址
数据结构算法与应用C++