- 想家
爆米花机
也许不同于大家对家乡的思念,我对家乡甚至是疯狂的不舍。还未踏出车站就感觉到幸福,我享受这里的夕阳、这里的浓烈柴火味、这里每一口家常菜。我是宅女,我贪恋家的安逸。刚刚踏出大学校门,初出茅庐,无法适应每年只能国庆和春节回家。我焦虑、失眠、无端发脾气,是无法适应工作的节奏,是无法接受我将一步步离开家乡的事实。我不想承认自己胸无大志,选择再次踏上征程。图片发自App
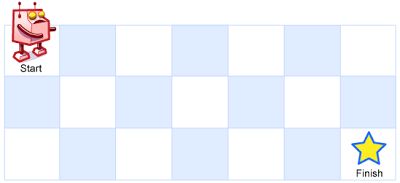
- element实现动态路由+面包屑
软件技术NINI
vue案例vue.js前端
el-breadcrumb是ElementUI组件库中的一个面包屑导航组件,它用于显示当前页面的路径,帮助用户快速理解和导航到应用的各个部分。在Vue.js项目中,如果你已经安装了ElementUI,就可以很方便地使用el-breadcrumb组件。以下是一个基本的使用示例:安装ElementUI(如果你还没有安装的话):你可以通过npm或yarn来安装ElementUI。bash复制代码npmi
- 微服务下功能权限与数据权限的设计与实现
nbsaas-boot
微服务java架构
在微服务架构下,系统的功能权限和数据权限控制显得尤为重要。随着系统规模的扩大和微服务数量的增加,如何保证不同用户和服务之间的访问权限准确、细粒度地控制,成为设计安全策略的关键。本文将讨论如何在微服务体系中设计和实现功能权限与数据权限控制。1.功能权限与数据权限的定义功能权限:指用户或系统角色对特定功能的访问权限。通常是某个用户角色能否执行某个操作,比如查看订单、创建订单、修改用户资料等。数据权限:
- 学点心理知识,呵护孩子健康
静候花开_7090
昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所,超越教育与技术的思考》的讲座。今天又重新学习了一遍,收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题,她说心理健康的一些基本命题,我们与我们通常的一些教育命题是不同的,她还举了几个例子,让我们明白我们原来以为的健康并非心理学上的健康。比如如果
- c++ 的iostream 和 c++的stdio的区别和联系
黄卷青灯77
c++算法开发语言iostreamstdio
在C++中,iostream和C语言的stdio.h都是用于处理输入输出的库,但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系:区别1.编程风格iostream(C++风格):C++标准库中的输入输出流类库,支持面向对象的输入输出操作。典型用法是cin(输入)和cout(输出),使用>操作符来处理数据。更加类型安全,支持用户自定义类型的输入输出。#includeintmain(){in
- swagger访问路径
igotyback
swagger
Swagger2.x版本访问地址:http://{ip}:{port}/{context-path}/swagger-ui.html{ip}是你的服务器IP地址。{port}是你的应用服务端口,通常为8080。{context-path}是你的应用上下文路径,如果应用部署在根路径下,则为空。Swagger3.x版本对于Swagger3.x版本(也称为OpenAPI3)访问地址:http://{ip
- 扫地机类清洁产品之直流无刷电机控制
悟空胆好小
清洁服务机器人单片机人工智能
扫地机类清洁产品之直流无刷电机控制1.1前言扫地机产品有很多的电机控制,滚刷电机1个,边刷电机1-2个,清水泵电机,风机一个,部分中高端产品支持抹布功能,也就是存在抹布盘电机,还有追觅科沃斯石头等边刷抬升电机,滚刷抬升电机等的,这些电机有直流有刷电机,直接无刷电机,步进电机,电磁阀,挪动泵等不同类型。电机的原理,驱动控制方式也不行。接下来一段时间的几个文章会作个专题分析分享。直流有刷电机会自动持续
- 2021-08-26
影幽
在生活中,女人与男人的感悟往往有所不同。人生最大的舞台就是生活,大幕随时都可能拉开,关键是你愿不愿意表演都无法躲避。在生活中,遇事不要急躁,不要急于下结论,尤其生气时不要做决断,要学会换位思考,大事化小小事化了,把复杂的事情尽量简单处理,千万不要把简单的事情复杂化。永远不要扭曲,别人善意,无药可救。昨天是张过期的支票,明天是张信用卡,只有今天才是现金,要善加利用!执着的攀登者不必去与别人比较自己的
- C#中使用split分割字符串
互联网打工人no1
c#
1、用字符串分隔:usingSystem.Text.RegularExpressions;stringstr="aaajsbbbjsccc";string[]sArray=Regex.Split(str,"js",RegexOptions.IgnoreCase);foreach(stringiinsArray)Response.Write(i.ToString()+"");输出结果:aaabbbc
- linux sdl windows.h,Windows下的SDL安装
奔跑吧linux内核
linuxsdlwindows.h
首先你要下载并安装SDL开发包。如果装在C盘下,路径为C:\SDL1.2.5如果在WINDOWS下。你可以按以下步骤:1.打开VC++,点击"Tools",Options2,点击directories选项3.选择"Includefiles"增加一个新的路径。"C:\SDL1.2.5\include"4,现在选择"Libaryfiles“增加"C:\SDL1.2.5\lib"现在你可以开始编写你的第
- Goolge earth studio 进阶4——路径修改与平滑
陟彼高冈yu
Googleearthstudio进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径,所以当我们通过这个关键帧时,不是一个生硬的角度,而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄,允许我们调整路径的形状。右键单击,我们可以选择“平滑路径”,这是默认的自动平滑算法,或者我们可
- Python教程:一文了解使用Python处理XPath
旦莫
Python进阶python开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath?2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
- LLM 词汇表
落难Coder
LLMsNLP大语言模型大模型llama人工智能
Contextwindow“上下文窗口”是指语言模型在生成新文本时能够回溯和参考的文本量。这不同于语言模型训练时所使用的大量数据集,而是代表了模型的“工作记忆”。较大的上下文窗口可以让模型理解和响应更复杂和更长的提示,而较小的上下文窗口可能会限制模型处理较长提示或在长时间对话中保持连贯性的能力。Fine-tuning微调是使用额外的数据进一步训练预训练语言模型的过程。这使得模型开始表示和模仿微调数
- 将cmd中命令输出保存为txt文本文件
落难Coder
Windowscmdwindow
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码,无可厚非,我们有必要保存我们的炼丹结果,但是复制命令行输出到txt是非常麻烦的,其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是:运行指令>输出到的文件名称或者具体保存路径测试下,我打开cmd并且ping一下百度:pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出:如果你再
- PHP环境搭建详细教程
好看资源平台
前端php
PHP是一个流行的服务器端脚本语言,广泛用于Web开发。为了使PHP能够在本地或服务器上运行,我们需要搭建一个合适的PHP环境。本教程将结合最新资料,介绍在不同操作系统上搭建PHP开发环境的多种方法,包括Windows、macOS和Linux系统的安装步骤,以及本地和Docker环境的配置。1.PHP环境搭建概述PHP环境的搭建主要分为以下几类:集成开发环境:例如XAMPP、WAMP、MAMP,这
- 山东大学小树林支教调研团青青仓木队——翟晓楠
山东大学青青仓木队
过了半年,又一次启程,又一次回到支教的初心之地。比起上一次的试探与不安,我更多了一丝稳重与熟练。心境、处境也都随着半个学期的过去而变得不同,半个学期中,身体上的,心理上的,太多的逆境让我变得步履维艰,曲曲折折,弯弯绕绕,我仿佛打不起精神,没有胃口,没有动力。感觉走的不顺畅的时候,支教这个旅程,给了我力量。自告奋勇承担起队长这一职务的我,从组织时的复杂和困难的经历,协调各种问题,从无到有,和校长和队
- 【加密社】Solidity 中的事件机制及其应用
加密社
闲侃区块链智能合约区块链
加密社引言在Solidity合约开发过程中,事件(Events)是一种非常重要的机制。它们不仅能够让开发者记录智能合约的重要状态变更,还能够让外部系统(如前端应用)监听这些状态的变化。本文将详细介绍Solidity中的事件机制以及如何利用不同的手段来触发、监听和获取这些事件。事件存储的地方当我们在Solidity合约中使用emit关键字触发事件时,该事件会被记录在区块链的交易收据中。具体而言,事件
- 探索OpenAI和LangChain的适配器集成:轻松切换模型提供商
nseejrukjhad
langchaineasyui前端python
#探索OpenAI和LangChain的适配器集成:轻松切换模型提供商##引言在人工智能和自然语言处理的世界中,OpenAI的模型提供了强大的能力。然而,随着技术的发展,许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具,集成了多种模型提供商,通过提供适配器,简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成,以便轻松切换模型提供商
- python八股文面试题分享及解析(1)
Shawn________
python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果:21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型,不仅仅改变
- 【目标检测数据集】卡车数据集1073张VOC+YOLO格式
熬夜写代码的平头哥∰
目标检测YOLO人工智能
数据集格式:PascalVOC格式+YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件)图片数量(jpg文件个数):1073标注数量(xml文件个数):1073标注数量(txt文件个数):1073标注类别数:1标注类别名称:["truck"]每个类别标注的框数:truck框数=1120总框数:1120使用标注工具:labelImg标注
- 人生的每一步路都算数
sheli
如果你想打工,一直靠打工赚钱,那你就会不断的希望自己变得更专业,不断的希望能够获得更好的工作机会,升职加薪。如果你的目标志不在此,而是拥有自己的企业,那你的选择就会出现差别。在认真打工的人眼里,会“不务正业”,会总是选择不同岗位,甚至放弃高薪机会。但是这背后都是有更加长远的规划。成功富人所必需的管理技能包括:1.对现金流的管理。2.对系统的管理。3.对人员的管理。所以,在没有获得这些能力之前,只要
- 大伟说成语之唉声叹气
求索大伟
*大伟说成语*【唉声叹气】叹气:因心里不痛快或不如意而吐出长气,发出声音。因为痛苦、憋闷或感伤而发出叹息的声音。【大伟说】情绪外露,非人类所特有,动物亦有情绪,悲哀和欢乐所表示的情绪亦是不一样的,会嗷嗷大叫也会低吟痛哭。不同的是,人类的情绪更复杂,更多样,更丰富。唉声叹气,可以说是最基础的情绪,因为无奈而举足无措,不知该如何如何化解,只有独自一人慢慢承受,长吁短叹不知如何是好,其实是无能无力的表现
- 走向以教育叙事为载体的教育叙事研究
666小飞鱼
今天我读了吴松超老师的《给教师的68条建写作建议》中的第23条《如何通过教育叙事走向研究》,吴老师在文中与我们分享了一个德育案例,这是一个反面的案例,意在告知我们在处理问题时,不能就考虑的点太窄,思考要全面。走向教育叙事研究,教师要有敏锐的“感知力”,这个感知力来自于背后专业知识的支撑,思维能力以及广阔的视野和见识等。所以对于同一件事处理方法不同,这个就是教师背后“敏锐力”的不同造成的,也就是说是
- 2023-10-22
奥雷里亚诺第n
昨天在B站看到关于猫喜欢挠人的视频,视频教导说猫挠人的话就抓住它的后脖颈然后用手打打挠人的那个爪子。视频本身没什么,但评论区却炸开了锅(真是符合挑食者厌食心理)。令我印象最深刻的一个甚至上升到了关于我是谁这种终极问题。它说,猫就是畜生,它挠人就打它别惯着它,反正我六道轮回成了人就应该保持人的高贵,谁都别想来打破。我顿时汗颜,但看到下面全是类似的言论只不过后面的理由各有不同,本来想骂人的心都凉了一半
- 没有邀请码怎么注册买手妈妈?
氧惠评测
买手妈妈怎么注册小编为大家带来买手妈妈没有邀请码怎么注册。打开买手妈妈APP,点击“马上注册”,输入邀请信息“邀请码”点击下一步,没有邀请码是登录不上的,所以这个必须要填写,那我们没有怎么办?填写成功就可以登录下一步。这里面有手机登录和淘宝登录,手机登录以后也需要用淘宝授权的,所以基本上都是淘宝登录。购物、看电影、点外卖、用氧惠APP!更优惠!氧惠(全网优惠上氧惠)——是与以往完全不同的抖客+淘客
- 钢筋长度超限检测检数据集VOC+YOLO格式215张1类别
futureflsl
数据集YOLO深度学习机器学习
数据集格式:PascalVOC格式+YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件)图片数量(jpg文件个数):215标注数量(xml文件个数):215标注数量(txt文件个数):215标注类别数:1标注类别名称:["iron"]每个类别标注的框数:iron框数=215总框数:215使用标注工具:labelImg标注规则:对类别进
- 数据仓库——维度表一致性
墨染丶eye
背诵数据仓库
数据仓库基础笔记思维导图已经整理完毕,完整连接为:数据仓库基础知识笔记思维导图维度一致性问题从逻辑层面来看,当一系列星型模型共享一组公共维度时,所涉及的维度称为一致性维度。当维度表存在不一致时,短期的成功难以弥补长期的错误。维度时确保不同过程中信息集成起来实现横向钻取货活动的关键。造成横向钻取失败的原因维度结构的差别,因为维度的差别,分析工作涉及的领域从简单到复杂,但是都是通过复杂的报表来弥补设计
- 第六集如何安装CentOS7.0,3分钟学会centos7安装教程
date分享
从光盘引导系统按回车键继续进入引导程序安装界面,选择语言这里选择简体中文版点击继续选择桌面安装下面给系统分区选择磁盘,点击完成选择基本分区,点击加号swap分区,大小填内存的两倍在选择根分区,使用所有可用的磁盘空间选择文件系统ext4点击完成,点击开始安装设置root密码,点击完成设置普通用户和密码,点击完成整个过程持续八分钟左右根据个人配置不同,时间长短不同好,现在点击重启系统进入重启状态点击本
- Python爬虫解析工具之xpath使用详解
eqa11
python爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中,数据提取是一个至关重要的环节。xpath作为一门
- Redis系列:Geo 类型赋能亿级地图位置计算
Ly768768
redisbootstrap数据库
1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构,它是基于不同业务场景而设计的:动态字符串(REDIS_STRING):整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
- apache 安装linux windows
墙头上一根草
apacheinuxwindows
linux安装Apache 有两种方式一种是手动安装通过二进制的文件进行安装,另外一种就是通过yum 安装,此中安装方式,需要物理机联网。以下分别介绍两种的安装方式
通过二进制文件安装Apache需要的软件有apr,apr-util,pcre
1,安装 apr 下载地址:htt
- fill_parent、wrap_content和match_parent的区别
Cb123456
match_parentfill_parent
fill_parent、wrap_content和match_parent的区别:
1)fill_parent
设置一个构件的布局为fill_parent将强制性地使构件扩展,以填充布局单元内尽可能多的空间。这跟Windows控件的dockstyle属性大体一致。设置一个顶部布局或控件为fill_parent将强制性让它布满整个屏幕。
2) wrap_conte
- 网页自适应设计
天子之骄
htmlcss响应式设计页面自适应
网页自适应设计
网页对浏览器窗口的自适应支持变得越来越重要了。自适应响应设计更是异常火爆。再加上移动端的崛起,更是如日中天。以前为了适应不同屏幕分布率和浏览器窗口的扩大和缩小,需要设计几套css样式,用js脚本判断窗口大小,选择加载。结构臃肿,加载负担较大。现笔者经过一定时间的学习,有所心得,故分享于此,加强交流,共同进步。同时希望对大家有所
- [sql server] 分组取最大最小常用sql
一炮送你回车库
SQL Server
--分组取最大最小常用sql--测试环境if OBJECT_ID('tb') is not null drop table tb;gocreate table tb( col1 int, col2 int, Fcount int)insert into tbselect 11,20,1 union allselect 11,22,1 union allselect 1
- ImageIO写图片输出到硬盘
3213213333332132
javaimage
package awt;
import java.awt.Color;
import java.awt.Font;
import java.awt.Graphics;
import java.awt.image.BufferedImage;
import java.io.File;
import java.io.IOException;
import javax.imagei
- 自己的String动态数组
宝剑锋梅花香
java动态数组数组
数组还是好说,学过一两门编程语言的就知道,需要注意的是数组声明时需要把大小给它定下来,比如声明一个字符串类型的数组:String str[]=new String[10]; 但是问题就来了,每次都是大小确定的数组,我需要数组大小不固定随时变化怎么办呢? 动态数组就这样应运而生,龙哥给我们讲的是自己用代码写动态数组,并非用的ArrayList 看看字符
- pinyin4j工具类
darkranger
.net
pinyin4j工具类Java工具类 2010-04-24 00:47:00 阅读69 评论0 字号:大中小
引入pinyin4j-2.5.0.jar包:
pinyin4j是一个功能强悍的汉语拼音工具包,主要是从汉语获取各种格式和需求的拼音,功能强悍,下面看看如何使用pinyin4j。
本人以前用AscII编码提取工具,效果不理想,现在用pinyin4j简单实现了一个。功能还不是很完美,
- StarUML学习笔记----基本概念
aijuans
UML建模
介绍StarUML的基本概念,这些都是有效运用StarUML?所需要的。包括对模型、视图、图、项目、单元、方法、框架、模型块及其差异以及UML轮廓。
模型、视与图(Model, View and Diagram)
&
- Activiti最终总结
avords
Activiti id 工作流
1、流程定义ID:ProcessDefinitionId,当定义一个流程就会产生。
2、流程实例ID:ProcessInstanceId,当开始一个具体的流程时就会产生,也就是不同的流程实例ID可能有相同的流程定义ID。
3、TaskId,每一个userTask都会有一个Id这个是存在于流程实例上的。
4、TaskDefinitionKey和(ActivityImpl activityId
- 从省市区多重级联想到的,react和jquery的差别
bee1314
jqueryUIreact
在我们的前端项目里经常会用到级联的select,比如省市区这样。通常这种级联大多是动态的。比如先加载了省,点击省加载市,点击市加载区。然后数据通常ajax返回。如果没有数据则说明到了叶子节点。 针对这种场景,如果我们使用jquery来实现,要考虑很多的问题,数据部分,以及大量的dom操作。比如这个页面上显示了某个区,这时候我切换省,要把市重新初始化数据,然后区域的部分要从页面
- Eclipse快捷键大全
bijian1013
javaeclipse快捷键
Ctrl+1 快速修复(最经典的快捷键,就不用多说了)Ctrl+D: 删除当前行 Ctrl+Alt+↓ 复制当前行到下一行(复制增加)Ctrl+Alt+↑ 复制当前行到上一行(复制增加)Alt+↓ 当前行和下面一行交互位置(特别实用,可以省去先剪切,再粘贴了)Alt+↑ 当前行和上面一行交互位置(同上)Alt+← 前一个编辑的页面Alt+→ 下一个编辑的页面(当然是针对上面那条来说了)Alt+En
- js 笔记 函数
征客丶
JavaScript
一、函数的使用
1.1、定义函数变量
var vName = funcation(params){
}
1.2、函数的调用
函数变量的调用: vName(params);
函数定义时自发调用:(function(params){})(params);
1.3、函数中变量赋值
var a = 'a';
var ff
- 【Scala四】分析Spark源代码总结的Scala语法二
bit1129
scala
1. Some操作
在下面的代码中,使用了Some操作:if (self.partitioner == Some(partitioner)),那么Some(partitioner)表示什么含义?首先partitioner是方法combineByKey传入的变量,
Some的文档说明:
/** Class `Some[A]` represents existin
- java 匿名内部类
BlueSkator
java匿名内部类
组合优先于继承
Java的匿名类,就是提供了一个快捷方便的手段,令继承关系可以方便地变成组合关系
继承只有一个时候才能用,当你要求子类的实例可以替代父类实例的位置时才可以用继承。
在Java中内部类主要分为成员内部类、局部内部类、匿名内部类、静态内部类。
内部类不是很好理解,但说白了其实也就是一个类中还包含着另外一个类如同一个人是由大脑、肢体、器官等身体结果组成,而内部类相
- 盗版win装在MAC有害发热,苹果的东西不值得买,win应该不用
ljy325
游戏applewindowsXPOS
Mac mini 型号: MC270CH-A RMB:5,688
Apple 对windows的产品支持不好,有以下问题:
1.装完了xp,发现机身很热虽然没有运行任何程序!貌似显卡跑游戏发热一样,按照那样的发热量,那部机子损耗很大,使用寿命受到严重的影响!
2.反观安装了Mac os的展示机,发热量很小,运行了1天温度也没有那么高
&nbs
- 读《研磨设计模式》-代码笔记-生成器模式-Builder
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/**
* 生成器模式的意图在于将一个复杂的构建与其表示相分离,使得同样的构建过程可以创建不同的表示(GoF)
* 个人理解:
* 构建一个复杂的对象,对于创建者(Builder)来说,一是要有数据来源(rawData),二是要返回构
- JIRA与SVN插件安装
chenyu19891124
SVNjira
JIRA安装好后提交代码并要显示在JIRA上,这得需要用SVN的插件才能看见开发人员提交的代码。
1.下载svn与jira插件安装包,解压后在安装包(atlassian-jira-subversion-plugin-0.10.1)
2.解压出来的包里下的lib文件夹下的jar拷贝到(C:\Program Files\Atlassian\JIRA 4.3.4\atlassian-jira\WEB
- 常用数学思想方法
comsci
工作
对于搞工程和技术的朋友来讲,在工作中常常遇到一些实际问题,而采用常规的思维方式无法很好的解决这些问题,那么这个时候我们就需要用数学语言和数学工具,而使用数学工具的前提却是用数学思想的方法来描述问题。。下面转帖几种常用的数学思想方法,仅供学习和参考
函数思想
把某一数学问题用函数表示出来,并且利用函数探究这个问题的一般规律。这是最基本、最常用的数学方法
- pl/sql集合类型
daizj
oracle集合typepl/sql
--集合类型
/*
单行单列的数据,使用标量变量
单行多列数据,使用记录
单列多行数据,使用集合(。。。)
*集合:类似于数组也就是。pl/sql集合类型包括索引表(pl/sql table)、嵌套表(Nested Table)、变长数组(VARRAY)等
*/
/*
--集合方法
&n
- [Ofbiz]ofbiz初用
dinguangx
电商ofbiz
从github下载最新的ofbiz(截止2015-7-13),从源码进行ofbiz的试用
1. 加载测试库
ofbiz内置derby,通过下面的命令初始化测试库
./ant load-demo (与load-seed有一些区别)
2. 启动内置tomcat
./ant start
或
./startofbiz.sh
或
java -jar ofbiz.jar
&
- 结构体中最后一个元素是长度为0的数组
dcj3sjt126com
cgcc
在Linux源代码中,有很多的结构体最后都定义了一个元素个数为0个的数组,如/usr/include/linux/if_pppox.h中有这样一个结构体: struct pppoe_tag { __u16 tag_type; __u16 tag_len; &n
- Linux cp 实现强行覆盖
dcj3sjt126com
linux
发现在Fedora 10 /ubutun 里面用cp -fr src dest,即使加了-f也是不能强行覆盖的,这时怎么回事的呢?一两个文件还好说,就输几个yes吧,但是要是n多文件怎么办,那还不输死人呢?下面提供三种解决办法。 方法一
我们输入alias命令,看看系统给cp起了一个什么别名。
[root@localhost ~]# aliasalias cp=’cp -i’a
- Memcached(一)、HelloWorld
frank1234
memcached
一、简介
高性能的架构离不开缓存,分布式缓存中的佼佼者当属memcached,它通过客户端将不同的key hash到不同的memcached服务器中,而获取的时候也到相同的服务器中获取,由于不需要做集群同步,也就省去了集群间同步的开销和延迟,所以它相对于ehcache等缓存来说能更好的支持分布式应用,具有更强的横向伸缩能力。
二、客户端
选择一个memcached客户端,我这里用的是memc
- Search in Rotated Sorted Array II
hcx2013
search
Follow up for "Search in Rotated Sorted Array":What if duplicates are allowed?
Would this affect the run-time complexity? How and why?
Write a function to determine if a given ta
- Spring4新特性——更好的Java泛型操作API
jinnianshilongnian
spring4generic type
Spring4新特性——泛型限定式依赖注入
Spring4新特性——核心容器的其他改进
Spring4新特性——Web开发的增强
Spring4新特性——集成Bean Validation 1.1(JSR-349)到SpringMVC
Spring4新特性——Groovy Bean定义DSL
Spring4新特性——更好的Java泛型操作API
Spring4新
- CentOS安装JDK
liuxingguome
centos
1、行卸载原来的:
[root@localhost opt]# rpm -qa | grep java
tzdata-java-2014g-1.el6.noarch
java-1.7.0-openjdk-1.7.0.65-2.5.1.2.el6_5.x86_64
java-1.6.0-openjdk-1.6.0.0-11.1.13.4.el6.x86_64
[root@localhost
- 二分搜索专题2-在有序二维数组中搜索一个元素
OpenMind
二维数组算法二分搜索
1,设二维数组p的每行每列都按照下标递增的顺序递增。
用数学语言描述如下:p满足
(1),对任意的x1,x2,y,如果x1<x2,则p(x1,y)<p(x2,y);
(2),对任意的x,y1,y2, 如果y1<y2,则p(x,y1)<p(x,y2);
2,问题:
给定满足1的数组p和一个整数k,求是否存在x0,y0使得p(x0,y0)=k?
3,算法分析:
(
- java 随机数 Math与Random
SaraWon
javaMathRandom
今天需要在程序中产生随机数,知道有两种方法可以使用,但是使用Math和Random的区别还不是特别清楚,看到一篇文章是关于的,觉得写的还挺不错的,原文地址是
http://www.oschina.net/question/157182_45274?sort=default&p=1#answers
产生1到10之间的随机数的两种实现方式:
//Math
Math.roun
- oracle创建表空间
tugn
oracle
create temporary tablespace TXSJ_TEMP
tempfile 'E:\Oracle\oradata\TXSJ_TEMP.dbf'
size 32m
autoextend on
next 32m maxsize 2048m
extent m
- 使用Java8实现自己的个性化搜索引擎
yangshangchuan
javasuperword搜索引擎java8全文检索
需要对249本软件著作实现句子级别全文检索,这些著作均为PDF文件,不使用现有的框架如lucene,自己实现的方法如下:
1、从PDF文件中提取文本,这里的重点是如何最大可能地还原文本。提取之后的文本,一个句子一行保存为文本文件。
2、将所有文本文件合并为一个单一的文本文件,这样,每一个句子就有一个唯一行号。
3、对每一行文本进行分词,建立倒排表,倒排表的格式为:词=包含该词的总行数N=行号