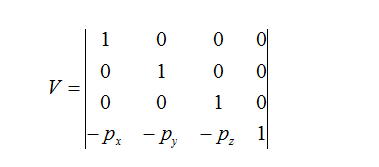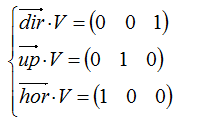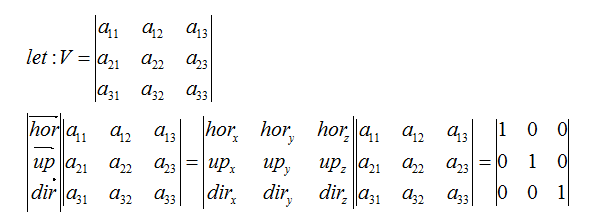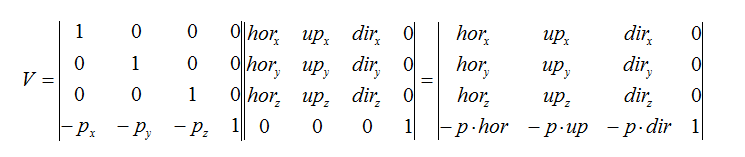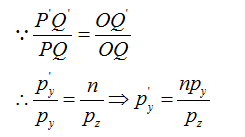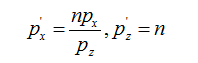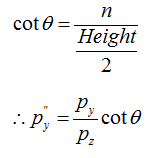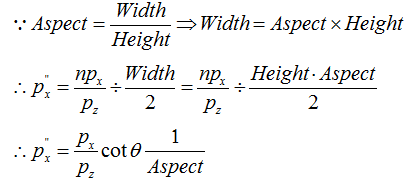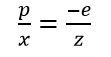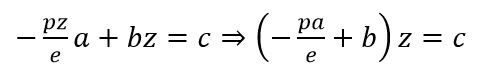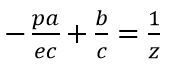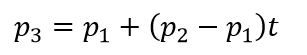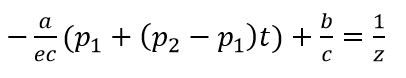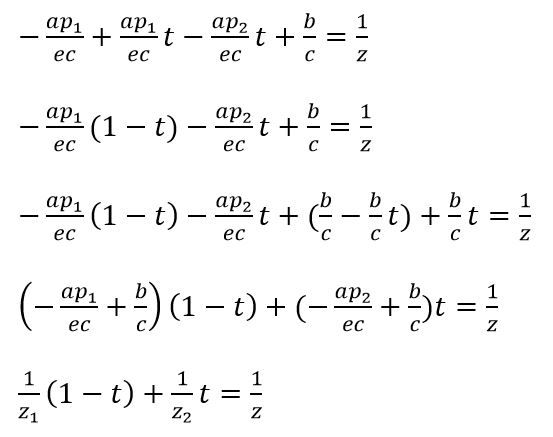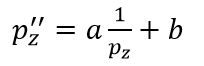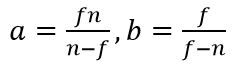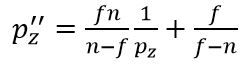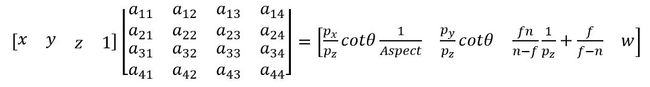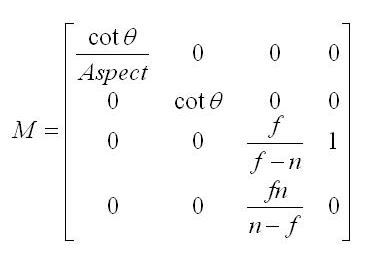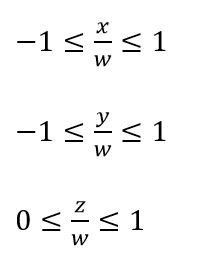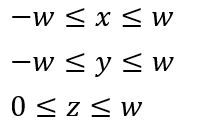顶点空间(Model Space)->世界空间(World Space)
从顶点空间到世界空间的变换实际上就是平移、旋转和缩放的组合,如果用过Unity,你会发现Transform组件中对应的Position、Rotation和Scale对应的就是这平移、旋转和缩放变换。
所以我们可以用之前的编写数学库轻易的构造出一个世界变换矩阵(World Transform)。
世界空间(World Space)->相机空间(Camera Space)
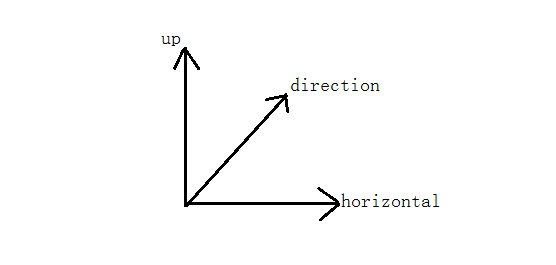
这一步我们要根据摄像机(Camera)的位置和朝向来构造一个视图变换矩阵(View Transform),摄像机的三个方向分别为direction,up和horizontal,其中摄像机的位置、三个朝向中的direction和up需要我们手动制定,水平方向horizontal可以通过direction和up向量做叉积得到
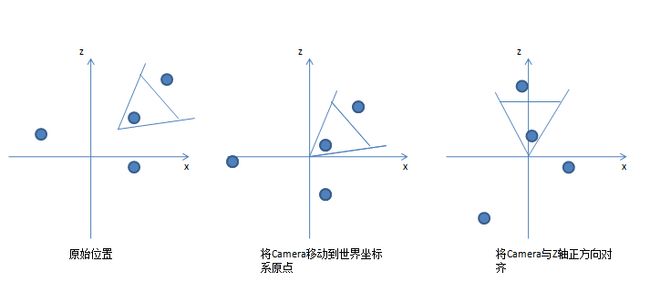
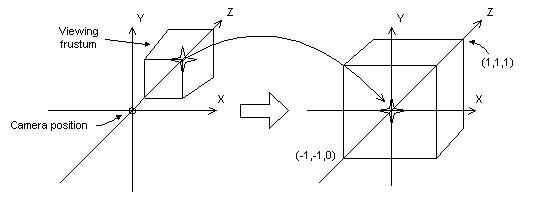
视图变换矩阵的作用是将整个世界变为“以摄像机为中心”,下图形象的解释了什么是以“摄像机为中心”
通过上面这张图我们知道,整个视图变化的过程分为两步:
- 将相机移动到世界坐标原点
- 将相机与z轴正方向对齐
设V为视图变换矩阵,dir,up和hor分别代表摄像机的direction,up和horizontal三个方向的基向量
先考虑平移的情况,根据摄像机的位置p我们只需要把它平移回原点就好了
然后考虑把相机与z轴正方向对齐,所谓对齐,就是说使得基向量两两正交且为单位向量,需要注意,这里的三个基向量都是相对于世界坐标系的,那么最简单的一种情况就是:
把②中向量展开成分量并写成一个等式
首先摄像机的三个基向量无论怎么设置都是两两正交的,所以由hor,up和dir组成的矩阵是一个正交矩阵
如果矩阵A是正交矩阵,那么矩阵A的逆矩阵等于矩阵A的转置。
③的右边是一个单位矩阵,所以
最后将两个矩阵相乘,组合成最终的视图变换矩阵
相机空间(Camera Space)->裁剪空间(Clip Space)
这个阶段要做的就是把视锥体变为长方体(正方体),然后把空间中的点投影到变换后的视锥的近裁剪平面上,变换视锥体的过程中场景内的顶点也要发生相应的变化,而透视矩阵要做的就是变换场景中的顶点。
从图中可以发现,在变换的过程中,近处的点之间的距离被拉大了,而远处的点之间的距离被相对地缩小了,这也就是透视变换产生“近大远小”感觉的原因。
上面的描述可以帮助你感性的理解这个过程。实际在计算的时候我们要则是先将空间中的点直接投影在近裁剪平面上,然后再在该屏幕上进行缩放的。
变换后,x坐标和y坐标表示的是点最终在屏幕上的位置的归一化坐标,其次坐标中的z分量会被映射到[0,1],用来进行顶点剔除,w分量则会存储顶点的深度信息。
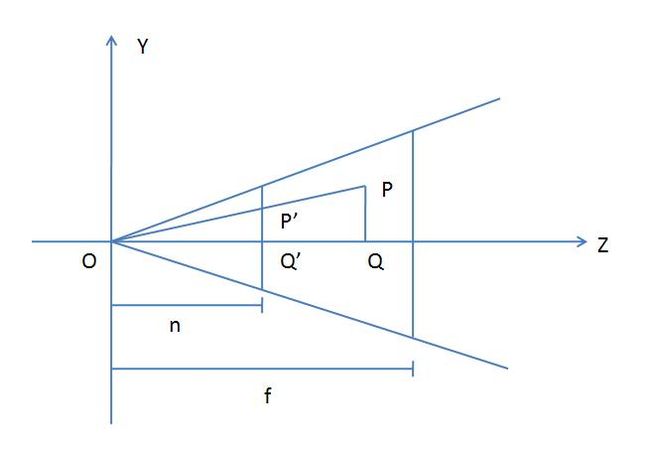
首先考虑把点先投影到近裁剪平面上
三角形PQO和三角形P'Q'O相似,并且近裁剪平面到原点的距离是知道的,所以可以求出P'点的坐标
求出P'点的y坐标后同理可以求出其x坐标
接下来考虑将P'在近裁剪平面上进行缩放
变换之前的近裁剪平面的宽和高并不是2(而是你渲染出来缓慢的宽和高),首先按屏幕大小进行缩放求P''点的y坐标
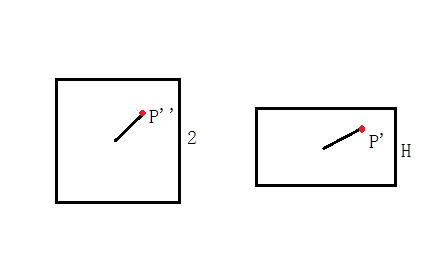
相机的视角与近裁剪屏幕的关系如下图
我们可以利用θ角来消去①中的Height
同理可以求的P''点中的x坐标,这里消去Width的时候还需要利用屏幕宽高比Aspect
但是还有一个问题,PP'点上所有的点变化得到的坐标都相同,那么怎么知道到底要渲染哪一个点呢?一般来说只会渲染离我们最近的点,即z值最小的点,即通过z值来存储点的深度来告诉我们哪些点在前面哪些在后面,方便渲染的时候进行处理。
在后面进行光栅化的时候,我们需要对三角形的顶点进行插值计算以求得实际渲染时三角形内部某个点的纹理坐标,如果直接进行线性插值,产生的图像是不正确的。
这张图告诉我们在插值的时候,屏幕上的x是等距离变化,如果进行线性插值,那么采样得到的点的纹理分布也是线性的,但实际上纹理的分布是不均匀的
考虑(x,z)是直线上的一点,从相机原点发射一条射线到这个点上,射线与近裁剪平面会有一个交点,假设这个交点的z坐标是-e(这张图引用于<
由三角形相似可得(和前面的计算原理相同)
设直线(x1,z1)(x2,z2)的方程为ax+bz=c,将①带入直线方程,消去x,得到
然后改写②为下面的形式
假设我们对(p1,-e)(p2,-e)之间进行插值得到点(p3,-e),那么有:
把④带入③得到
对⑤进行下列变化即可得到
这样就证明了对空间上纹理坐标与1/z是线性的关系,所以为了便于计算,我们将变化后新的点的z坐标用1/z做映射
z坐标的取值范围是从近裁剪平面到原点的距离n到远裁剪平面到原点的距离f,同时变换后的z''的范围是[0,1],将其代入①得到
再将②代入①,得到
这样我们通过计算得到了变换后的顶点的坐标
由于其次坐标的w分量表示了物体在投影时的深度信息,在变换为普通坐标的时候需要将x,y,z坐标除以w,所以我们在对①右侧的其次坐标的每一个分量乘以Pz并不会改变坐标的大小,得到
令w=1解上述方程,可以得到透视变换矩阵为
CVV裁剪
完成了上述三个变换后,还需要进行裁剪工作,将不再变换后的长方体内的顶点给剔除
变换完成后的顶点为其次坐标,二长方体的x,y的取值为-11,z的取值为01,那么有
不等式两边同时乘以w可以得到
这样在进行顶点剔除的时候就不需要进行除法运算了,当剔除掉不在摄像机范围内的点后进行其次除法操作,得到像素点的归一化坐标,然后根据归一化坐标以及屏幕的宽高就能得到顶点在屏幕中实际的位置了。