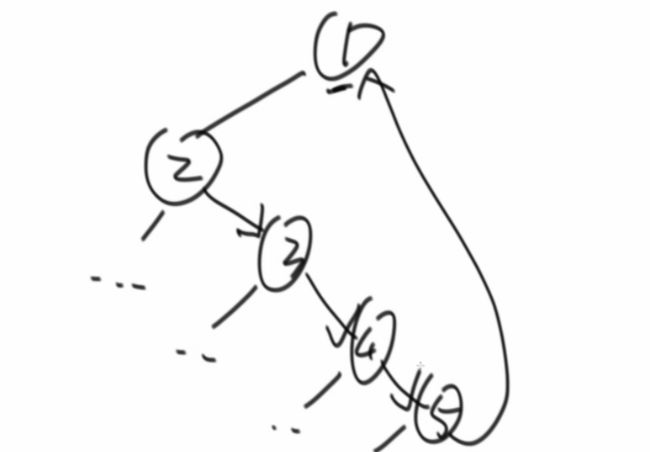
思想:
遵循以下原则
1.当前结点cur没有左子树,当前结点cur向右移动
2.当前结点cur有左子树,找到当前结点左子树的最右结点
如果左子树的最右结点的右子树为空,那么将本来指向空的最右结点指向当前结点cur,然后当前结点向左移动
如果当前结点cur左子树的最右结点指向当前结点cur,让最右孩子指向空,cur向右移动。
遍历顺序如下图
总结:在树中,对于任何一个有左子树的结点会两次回到自己,对于没有左子树的结点,只会到达结点一次,顺序是先遍历当前结点,然后左子树,然后回到当前结点,然后右子树。当前结点一定是我左子树最右孩子的后继结点。
代码:
public static void morrisIn(Node head) {
if (head == null) {
return;
}
//当前结点
Node cur1 = head;
Node cur2 = null;
while (cur1 != null) {
//当前结点的左孩子
cur2 = cur1.left;
if (cur2 != null) {
//当左孩子的右子树不是空切不是cur1时一直向右移动
while (cur2.right != null && cur2.right != cur1) {
cur2 = cur2.right;
}
//cur2最右子树为空,就让它指向cur1,然后cur1左移
if (cur2.right == null) {
cur2.right = cur1;
cur1 = cur1.left;
//跳入大循环的下一次
continue;
} else {
cur2.right = null;
}
}
//包含两种情况,一是没左子树直接右移,二是第二次到达当前结点(在执行完cur2.right=null)
cur1 = cur1.right;
}
System.out.println();
}
由Morris变形的二叉树遍历
先序:
#######思想:
我们观察Morris遍历的结果和分析可知,Morris遍历其实就是不加打印的二叉树遍历,把打印语句插入到里面就可以改写成先序中序或者后序
改成先序,即第一次到达当前结点的时候打印,第二次到达不打印,而在代码中怎么体现呢,当左子树最右结点第一次指向cur时,说明cur结点第一次到达,就打印,或者当前结点的左子树为空,也代表了第一次到达且只能到达一次打印,就在代码里加上两个打印语句即可
#######代码:
public static void morrisPre(Node head) {
if (head == null) {
return;
}
Node cur1 = head;
Node cur2 = null;
while (cur1 != null) {
cur2 = cur1.left;
if (cur2 != null) {
while (cur2.right != null && cur2.right != cur1) {
cur2 = cur2.right;
}
if (cur2.right == null) {
cur2.right = cur1;
//代表第一次到达打印
System.out.print(cur1.value + " ");
cur1 = cur1.left;
continue;
} else {
cur2.right = null;
}
} else {
//代表没有左子树打印
System.out.print(cur1.value + " ");
}
cur1 = cur1.right;
}
System.out.println();
}
中序:
#######思想:
中序即第二次到达的时候再打印或者没有左子树直接打印,我们经过分析,什么时候满足以上两种情况呢,就是当cur要右移之前,每当cur右移都包含了第二次到达或者没有左子树,所以就在cur右移的代码前加上打印语句即可
#######代码:
public static void morrisIn(Node head) {
if (head == null) {
return;
}
//当前结点
Node cur1 = head;
Node cur2 = null;
while (cur1 != null) {
//当前结点的左孩子
cur2 = cur1.left;
if (cur2 != null) {
while (cur2.right != null && cur2.right != cur1) {
cur2 = cur2.right;
}
if (cur2.right == null) {
cur2.right = cur1;
cur1 = cur1.left;
//跳入大循环的下一次
continue;
} else {
cur2.right = null;
}
}
//这里!!!!!
System.out.print(cur1.value + " ");
cur1 = cur1.right;
}
System.out.println();
}
后序:
#######思想:
基本思路是逆序打印第二次到达结点的右边界,第二次到达结点的打印完了之后,逆序打印整个二叉树的有边界
有边界就是,当前结点的左子树的所有右结点一直到头如下图
注意在逆序的时候,第一轮循环只是改变结点,没改变指向,到了下一轮循环才改变指针的方向
单链表操作 如果是比如from.right = pre 这就表明的是from指向pre 你可以看成 from->right=pre通俗理解为from往右指是pre,然后比如from=next 就相当于,from指向next指向的结点,就相当于from和next指向同一个结点
当a.next在等式的左边时,比如a.next=b,就理解为a的下一个节点是b,当a.next结点在右边时比如,b=a.next,就相当于b指向了a.next的位置
#######代码:
public static void morrisPos(Node head) {
if (head == null) {
return;
}
Node cur1 = head;
Node cur2 = null;
while (cur1 != null) {
cur2 = cur1.left;
if (cur2 != null) {
while (cur2.right != null && cur2.right != cur1) {
cur2 = cur2.right;
}
if (cur2.right == null) {
cur2.right = cur1;
cur1 = cur1.left;
continue;
} else {
cur2.right = null;
printEdge(cur1.left);
}
}
cur1 = cur1.right;
}
printEdge(head);
System.out.println();
}
public static void printEdge(Node head) {
Node tail = reverseEdge(head);
Node cur = tail;
while (cur != null) {
System.out.print(cur.value + " ");
cur = cur.right;
}
reverseEdge(tail);
}
public static Node reverseEdge(Node from) {
Node pre = null;
Node next = null;
while (from != null) {
next = from.right;
from.right = pre;
pre = from;
from = next;
}
return pre;
}