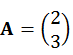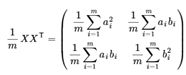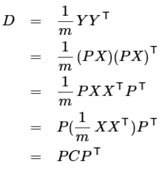一、理论篇:
为书写方便,加粗的字母表示向量。
如果想像力够好,完全可以想象出两个矩阵相乘的几何意义:将右边矩阵中每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间去。
比如我们常说的二维向量,
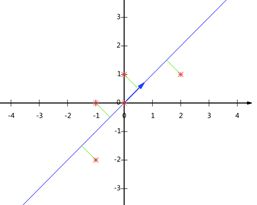
仅仅有这个条件,是不够来表示一个向量的,还默认了两个基向量(1,0)和(0,1),一个基向量可代表一个空间,在这里分别指x轴和y轴两个一维空间(在一维的空间里,(1,0),可以不写0的,直接写(1),数轴嘛)。二维向量正式A的表示方式应该是,拆开看分别是:第一行(1,0)xA,第二行(0,1)xA(当然你也可以理解为基向量的线性组合2x(1,0)'+3x(0,1)',目前在讨论变换的几何意义,总觉得用线性组合的方式不好想象。),于是第一行可想象为空间里的一个“箭头”A,被左乘了一下,(1,0)xA,变换到(1,0)的空间里去,变成了(2),(在x轴这个一维空间里,(1,0)或(2,3)里的0或3是没有必要写的),同样的道理,第二行y轴也是。
也可以不用(1,0),(0,1)基表示,可以换成其他基,不再累赘。
总结:
1.选择不同的基,可以对同一组数据给出不同的表示。
2.可以完全扩成一个空间的基对这一组数据的所有表示加起来,包含了这组数据的全部信息。
如果我们舍弃y轴空间,这就是降维。
当然,不能乱舍弃,降维的目的是为了舍弃那些没有多少用的数据,来保证减少数据量的同时,不降低数据的信息。
比如,
第一列和第三列线性相关,只要知道第一列,就等于知道了第三列,这个时候就可以舍弃第三行,变成
再回到几何意义,我们可以把二维数据通过上述分析分别变换(投射)到两个一维的基里,而基可以任意选。假设有一大串二维数据X(几何意义就是坐标里的一系列点),我们选一个一维基,把这些点进行投射到它的空间,如果选的足够好,这一个基就包含了大部分的数据信息,这样,只要选这一个基来表示所有数据就好了。
总结:
3.不一定要选全部的基去表示这组数据,用基表示后,信息多,就可以用,信息少,就可以舍弃。
而关键是,怎么选基?直观上看有两点:
(1)希望投影后的投影值尽可能分散,而这种分散程度,可用方差来表示。
(2)投影后,它们之间不存在线性关系,可用协方差来表示。
我们的目标就变成了:选择一组低纬基,让高维投在低维上,最离散、最不相关。正交时相关性为0,所以一般选正交基
拿上面的二维数据X举例子,我们要选一组基P,令X投射到P后(这个动作用公式来表示就是Y=P.X),得到的矩阵Y的方差最大,协方差最小。而把矩阵方差和协方差联系起来的,正好是协方差矩阵。
假设X:
而C=:
对角线表示方差,非对角线表示协方差。
其中方差(均值化零):
协方差(均值化零):
同样Y也有协方差矩阵。我们要做的,就是要找到P,使得Y协方差矩阵对角线(方差)最大,非对角线为0(协方差,不相关),满足这样的要求,不刚好是对角矩阵吗?于是:
这是什么?这就是求矩阵C的对角矩阵呀!!!
总结:
4.怎么选低维基?能让这组数据的协方差矩阵相似对角化。
有了P,问题就迎刃而解了。P的前k行组成的矩阵乘以数据矩阵X,便达到了降维的目的。
最后总结一下PCA的算法步骤:
设有m条n维的数据。
1.将原始数据按列组成n行m列矩阵X
2.将X的每一行进行零均值化
3.求X的协方差矩阵C
4.求C的特征值和特征向量
5.将特征向量按对应的特征值大小从上到下排列成矩阵,取前k行组成矩阵P
6.Y=PX即是降到k维后的数据
二、实现篇:
原本是想用matlab,毕竟对它比较熟。后来侥幸发现工作中自动化用的python也有不错的数据处理功能。电脑上没有matlab,但有现成的python环境,懒的人一般都会选择用现有的东西。
Python有着非常强大的科学计算库:
numpy~~基础计算库,多维数组处理
scipy~~基于numpy,用于数值计算等等,默认调用intel mkl(高度优化的数学库)
pandas~~强大的数据框,基于numpy
matplotlib~~绘图库,基于numpy,scipy
sklearn~~机器学习库,有各种机器学习算法
可以直接下载Anaconda,包含了大部分库。
把我自己的一张图片降维后,取前n=0,50,100,150,200,250,300,350,400行分别得到的图片如下:
(图片是300*400)
附上程序(程序都是自己写的,有点乱):
import numpy as np
from PIL import Image
import os,glob
import scipy.linalg as linA
#将矩阵零均值化
def zeroMean(dataMat):
meanVal=np.mean(dataMat,axis=0)
newData=dataMat-meanVal
return newData,meanVal
#将矩阵进行PCA降维,dataMat为需要降维的矩阵,n为选取前n个最大的特征值对应的特征向量
def pca(dataMat,n):
newData,meanVal=zeroMean(dataMat)#2.将X的每一行进行零均值化
covMat=np.cov(newData,rowvar=0) #3.求X的协方差矩阵C
#4.求C的特征值和特征向量
eigVals,eigVects=np.linalg.eig(np.mat(covMat))
eigValIndice=np.argsort(eigVals)
#5.将特征向量按对应的特征值大小从上到下排列成矩阵,取前n行组成矩阵P
n_eigValIndice=eigValIndice[-1:-(n+1):-1]
n_eigVect=eigVects[:,n_eigValIndice]
#6.Y=PX即是降到k维后的数据
lowDDataMat=newData*n_eigVect
reconMat=(lowDDataMat*n_eigVect.T)+meanVal#降维后的Y再加上之前零均值化所减去的平均值
return lowDDataMat,reconMat
#读取图片并转换为矩阵。1.将原始数据按列组成n行m列矩阵X
def ImageToMatrix(pictureName):
#读取图片
img = Image.open(pictureName)
#显示图片
#img.show()
width,height = img.size
img = img.convert("L")
data = img.getdata()
data = np.matrix(data,dtype='float')/255.0
#new_data = np.reshape(data,(width,height))
new_data = np.reshape(data,(height,width))
return new_data
#将矩阵转换为图片
def MatrixToImage(data):
data = data*255
new_img = Image.fromarray(data.astype(np.uint8))
return new_img
if __name__ == '__main__':
picture_path = os.getcwd()+'\\picture\\'
picture_save_path= picture_path+'save\\'
pictureName=picture_path+'Man.bmp'
dataMat=ImageToMatrix(pictureName)
n=0
for n in range(0,400,50):
lowDDataMat,reconMat=pca(dataMat,n)
new_img=MatrixToImage(reconMat)
#new_img.show()
new_img.save(picture_save_path+str(n)+'.bmp')
参考:
http://www.360doc.com/content/13/1124/02/9482_331688889.shtml